使用逻辑回归对信用卡诈骗分析
此次的数据集包括了 2013 年 9 月份两天时间内的信用卡交易数据,284807 笔交易中,一共有 492 笔 是欺诈行为。输入数据一共包括了 28 个特征 V1,V2,……V28 对应的取值,以及交易时间 Time 和交易金额 Amount。为了保护数据隐私,我们不知道 V1 到 V28 这些特征代表的具体含 义,只知道这 28 个特征值是通过 PCA 变换得到的结果。另外字段 Class 代表该笔交易的分类, Class=0 为正常(非欺诈),Class=1 代表欺诈。
因为284807笔交易中只有492笔是诈骗的,数据非常的不平衡,就算全部瞎猜是正常交易,准确率也可以达到98%,所以我们不能使用准确率来评价,这里我们使用统计 F1 值(综合精确率和召回率)。
数据探索
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import itertools
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, precision_recall_curve
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')
# 数据加载
data = pd.read_csv('F:/BaiduNetdiskDownload/DC/credit_fraud/creditcard.csv', encoding='utf-8')
# 查看数据
print(data.describe())
运行结果如下
Time V1 V2 V3 V4 \
count 284807.000000 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05
mean 94813.859575 3.919560e-15 5.688174e-16 -8.769071e-15 2.782312e-15
std 47488.145955 1.958696e+00 1.651309e+00 1.516255e+00 1.415869e+00
min 0.000000 -5.640751e+01 -7.271573e+01 -4.832559e+01 -5.683171e+00
25% 54201.500000 -9.203734e-01 -5.985499e-01 -8.903648e-01 -8.486401e-01
50% 84692.000000 1.810880e-02 6.548556e-02 1.798463e-01 -1.984653e-02
75% 139320.500000 1.315642e+00 8.037239e-01 1.027196e+00 7.433413e-01
max 172792.000000 2.454930e+00 2.205773e+01 9.382558e+00 1.687534e+01
V5 V6 V7 V8 V9 \
count 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05
mean -1.552563e-15 2.010663e-15 -1.694249e-15 -1.927028e-16 -3.137024e-15
std 1.380247e+00 1.332271e+00 1.237094e+00 1.194353e+00 1.098632e+00
min -1.137433e+02 -2.616051e+01 -4.355724e+01 -7.321672e+01 -1.343407e+01
25% -6.915971e-01 -7.682956e-01 -5.540759e-01 -2.086297e-01 -6.430976e-01
50% -5.433583e-02 -2.741871e-01 4.010308e-02 2.235804e-02 -5.142873e-02
75% 6.119264e-01 3.985649e-01 5.704361e-01 3.273459e-01 5.971390e-01
max 3.480167e+01 7.330163e+01 1.205895e+02 2.000721e+01 1.559499e+01
... V21 V22 V23 V24 \
count ... 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05
mean ... 1.537294e-16 7.959909e-16 5.367590e-16 4.458112e-15
std ... 7.345240e-01 7.257016e-01 6.244603e-01 6.056471e-01
min ... -3.483038e+01 -1.093314e+01 -4.480774e+01 -2.836627e+00
25% ... -2.283949e-01 -5.423504e-01 -1.618463e-01 -3.545861e-01
50% ... -2.945017e-02 6.781943e-03 -1.119293e-02 4.097606e-02
75% ... 1.863772e-01 5.285536e-01 1.476421e-01 4.395266e-01
max ... 2.720284e+01 1.050309e+01 2.252841e+01 4.584549e+00
V25 V26 V27 V28 Amount \
count 2.848070e+05 2.848070e+05 2.848070e+05 2.848070e+05 284807.000000
mean 1.453003e-15 1.699104e-15 -3.660161e-16 -1.206049e-16 88.349619
std 5.212781e-01 4.822270e-01 4.036325e-01 3.300833e-01 250.120109
min -1.029540e+01 -2.604551e+00 -2.256568e+01 -1.543008e+01 0.000000
25% -3.171451e-01 -3.269839e-01 -7.083953e-02 -5.295979e-02 5.600000
50% 1.659350e-02 -5.213911e-02 1.342146e-03 1.124383e-02 22.000000
75% 3.507156e-01 2.409522e-01 9.104512e-02 7.827995e-02 77.165000
max 7.519589e+00 3.517346e+00 3.161220e+01 3.384781e+01 25691.160000
Class
count 284807.000000
mean 0.001727
std 0.041527
min 0.000000
25% 0.000000
50% 0.000000
75% 0.000000
max 1.000000
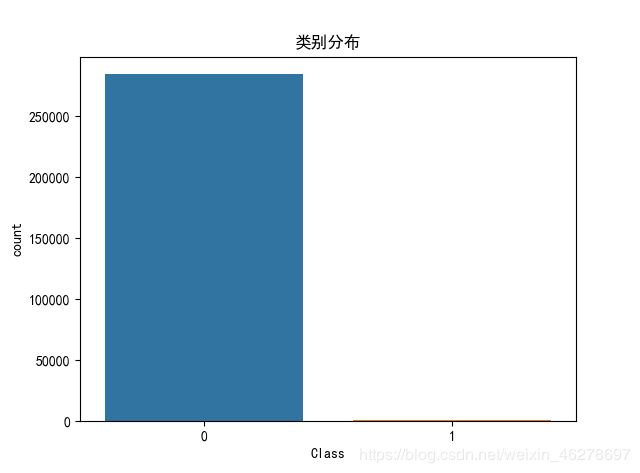
交易笔数,欺诈交易笔数可视化
# 设置plt正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
# 绘制类别分布
plt.figure()
ax = sns.countplot(x ='Class', data = data)
plt.title('类别分布')
plt.show()
# 显示交易笔数,欺诈交易笔数
num = len(data)
num_fraud = len(data[data['Class']==1])
print('总交易笔数: ', num)
print('诈骗交易笔数:', num_fraud)
print('诈骗交易比例:{:.6f}'.format(num_fraud/num))
# 欺诈和正常交易可视化
f, (ax1, ax2) = plt.subplots(2, 1, sharex=True, figsize=(15,8))
bins = 50
ax1.hist(data.Time[data.Class == 1], bins=bins, color= 'deeppink')
ax1.set_title('诈骗交易')
ax2.hist(data.Time[data.Class == 0], bins=bins, color= 'deepskyblue')
ax2.set_title('正常交易')
plt.xlabel('时间')
plt.ylabel('交易次数')
plt.show()
运行结果如下
总交易笔数: 284807
诈骗交易笔数: 492
诈骗交易比例:0.001727
特征选择
# 对Amount进行数据规范化
data['Amount_Norm'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1,1))
# 特征选择
y = np.array(data.Class.tolist())
data = data.drop(['Time','Amount','Class'],axis=1)
X = np.array(data.values)
# 准备训练集和测试集
train_x, test_x, train_y, test_y = train_test_split (X, y, test_size =0.1, random_state=33)
逻辑回归建模
# 逻辑回归分类
clf = LogisticRegression()
clf.fit(train_x, train_y)
predict_y = clf.predict(test_x)
# 预测样本的置信分数
score_y = clf.decision_function(test_x)
# 计算混淆矩阵
cm = confusion_matrix(test_y, predict_y)
class_names = [0, 1]
# 显示混淆矩阵
plt.figure()
plt.imshow(cm, interpolation = 'nearest', cmap=plt.cm.Blues) # 热度图
plt.title('Confusion matrix')
plt.colorbar() # 热度显示仪
tick_marks = np.arange(len(class_names)) # 坐标顺序
plt.xticks(tick_marks, class_names, rotation = 0) # 第一个是迭代对象,表示坐标的顺序,第二个是坐标显示的数值的数组
plt.yticks(tick_marks, class_names)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])) : # 显示数字直观些
plt.text(j, i, cm[i, j],
horizontalalignment = 'center',
color = 'white' if cm[i, j] > thresh else 'black')
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
显示模型评估分数
tp = cm[1, 1]
fn = cm[1, 0]
fp = cm[0, 1]
tn = cm[0, 0]
print('精确率: {:.3f}'.format(tp / (tp + fp)))
print('召回率: {:.3f}'.format(tp / (tp + fn)))
print('F1值: {:.3f}'.format(2 * (((tp / (tp + fp)) * (tp / (tp + fn))) / ((tp / (tp + fp)) + (tp / (tp + fn))))))
运行结果如下
精确率: 0.848
召回率: 0.650
F1值: 0.736
可以看出逻辑回归模型的F1值跟精确率,召回率的值都不错,这三个值最好的时候都为1,最差时候为0
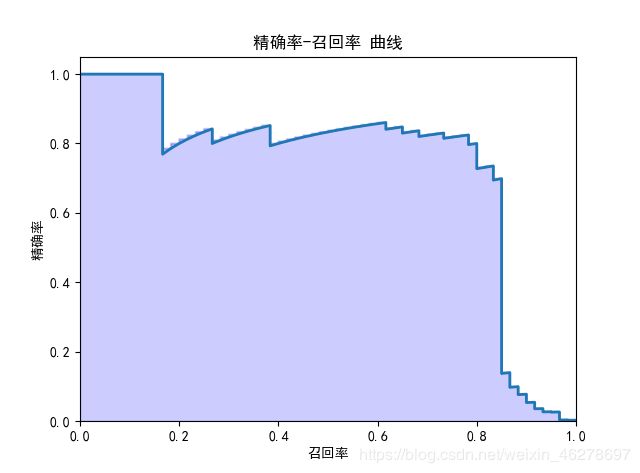
绘制精确率-召回率曲线
precision, recall, thresholds = precision_recall_curve(test_y, score_y)
plt.step(recall, precision, color='b', alpha=0.2, where='post')
plt.fill_between(recall, precision, step='post', alpha=0.2, color='b')
plt.plot(recall, precision, linewidth=2)
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xlabel('召回率')
plt.ylabel('精确率')
plt.title('精确率-召回率 曲线')
plt.show()
总结
在我们发现数据正负比例严重不平衡时,不能使用准确率来判断模型的好坏,而是使用F1 值(综合精确率和召回率)来判断模型的好坏