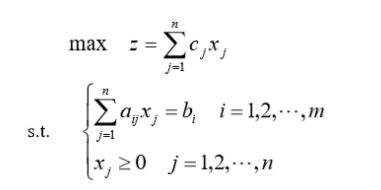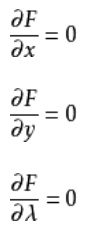人工智能与机器学习---线性规划和非线性规划求解

一、线性规划

1、线性规划的概念

线性规划(Linear Programming 简记 LP)是了运筹学中数学规划的一个重要分支。自从 1947 年 G. B. Dantzig 提出 求解线性规划的单纯形法以来，线性规划在理论上趋向成熟，在实用中由于计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划现代管理中经常采用的基本方法之一。 在解决实际问题时，需要把问题归结成一个线性规划数学模型，关键及难点在于选适当的决策变量建立恰当的模型，这直接影响到问题的求解。

线性规划问题的目标函数及约束条件均为线性函数；约束条件记为 s.t.(即 subject to)。目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以 是小于号也可以是大于号。

一般线性规划问题的（数学）标准型为

2、单纯形法

一般线性规划问题中当线性方程组的变量数大于方程个数，这时会有不定数量的解，而单纯形法是求解线性规划问题的通用方法。

具体步骤是，从线性方程组找出一个个的单纯形，每一个单纯形可以求得一组解，然后再判断该解使目标函数值是增大还是变小了，决定下一步选择的单纯形。通过优化迭代，直到目标函数实现最大或最小值。

换而言之，单纯形法就是秉承“保证每一次迭代比前一次更优”的基本思想：先找出一个基本可行解，对它进行鉴别，看是否是最优解；若不是，则按照一定法则转换到另一改进后更优的基本可行解，再鉴别；若仍不是，则再转换，按此重复进行。因基本可行解的个数有限，故经有限次转换必能得出问题的最优解。如果问题无最优解，也可用此法判别。

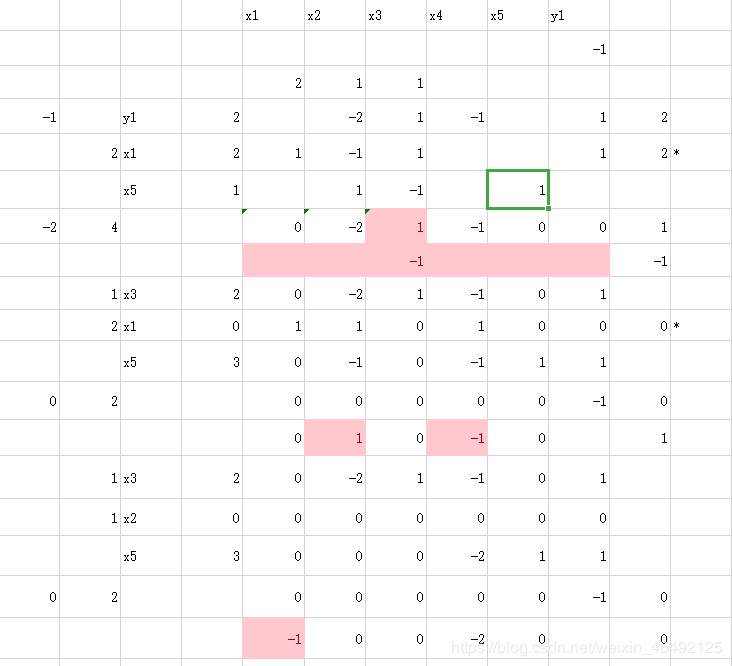
3、大M法

求解带有人工变量的线性规划问题，通常有两种方法：大M法和两阶段法。
大M法又称惩罚法，它是在目标函数中添加m个人工变量Mx（M是一个任意大的正数），同时在A矩阵中添加一个m阶单位矩阵。

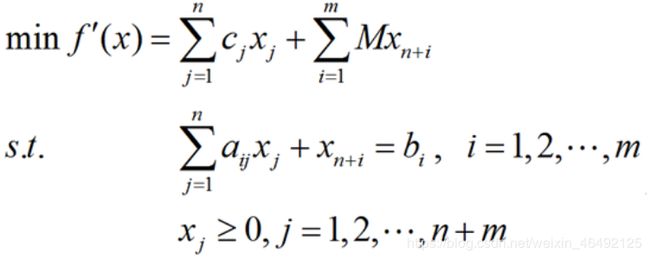
这样一来新的A矩阵中就有了一个mm满秩方阵，满足单纯形法求解的初始要求，但是若要得到最小值f(x),新添加的人工变量的值必然是0的，因为M可以是很大的数，如果Xn+1不为0，f(x)可能会很大，如果无法做到令人工变量取0值，那么原问题就无可行解。

需要注意的是，添加完人工变量之后，人工变量构成一组可行解的基变量，但单纯形初始矩阵要求基变量对应的检验数为0，故需要做行变换把基变量对应的检验数置0。

4、线性规划中大M法的excel求解

（1）题目

（2）Excel中的求解

（3）结果

推导得出：x1=0,x2=0,x3=2,max=2

5、利用python求解上述题目

（1）运行JupyterNotebook(Anaconda3)

（2）编写程序

A、python编程求解

# encoding=utf-8
import numpy as np  # python 矩阵操作lib
class Simplex():

    def __init__(self):
        self._A = ""  # 系数矩阵
        self._b = ""  #数组
        self._c = ''  # 约束
        self._B = ''  # 基变量的下标集合
        self.row = 0  # 约束个数

    def solve(self):
        # 读取文件内容，文件结构前两行分别为 变量数 和 约束条件个数
        # 接下来是系数矩阵
        # 然后是b数组
        # 然后是约束条件c
        # 假设线性规划形式是标准形式（都是等式）

        A = []
        b = []
        c = []

        self._A = np.array(A, dtype=float)
        self._b = np.array(b, dtype=float)
        self._c = np.array(c, dtype=float)
        self._A = np.array([[0,2,-1],[0,1,-1]],dtype=float)
        self._b = np.array([-2,1],dtype=float)
        self._A = np.array([[1,-1,1]])# 等式约束系数self._A，3x1维列向量
        self._b = np.array([2])# 等式约束系数self._b，1x1数值
        
        self._c = np.array([2,1,1],dtype=float)
        self._B = []
        self.row = len(self._b)
        self.var = len(self._c)
        (x, obj) = self.Simplex(self._A, self._b, self._c)
        self.pprint(x, obj, A)

    def pprint(self, x, obj, A):
        px = ['x_%d = %f' % (i + 1, x[i]) for i in range(len(x))]
        print(','.join(px))

        print('objective value is : %f' % obj)
        print('------------------------------')
        for i in range(len(A)):
            print('%d-th line constraint value is : %f' % (i + 1, x.dot(A[i])))

    def InitializeSimplex(self, A, b):

        b_min, min_pos = (np.min(b), np.argmin(b))  # 得到最小bi

        # 将bi全部转化成正数
        if (b_min < 0):
            for i in range(self.row):
                if i != min_pos:
                    A[i] = A[i] - A[min_pos]
                    b[i] = b[i] - b[min_pos]
            A[min_pos] = A[min_pos] * -1
            b[min_pos] = b[min_pos] * -1

        # 添加松弛变量
        slacks = np.eye(self.row)
        A = np.concatenate((A, slacks), axis=1)
        c = np.concatenate((np.zeros(self.var), np.ones(self.row)), axis=0)
        # 松弛变量全部加入基,初始解为b
        new_B = [i + self.var for i in range(self.row)]

        # 辅助方程的目标函数值
        obj = np.sum(b)

        c = c[new_B].reshape(1, -1).dot(A) - c
        c = c[0]
        # entering basis
        e = np.argmax(c)

        while c[e] > 0:
            theta = []
            for i in range(len(b)):
                if A[i][e] > 0:
                    theta.append(b[i] / A[i][e])
                else:
                    theta.append(float("inf"))

            l = np.argmin(np.array(theta))

            if theta[l] == float('inf'):
                print('unbounded')
                return False

            (new_B, A, b, c, obj) = self._PIVOT(new_B, A, b, c, obj, l, e)

            e = np.argmax(c)

        # 如果此时人工变量仍在基中，用原变量去替换之
        for mb in new_B:
            if mb >= self.var:
                row = mb - self.var
                i = 0
                while A[row][i] == 0 and i < self.var:
                    i += 1
                (new_B, A, b, c, obj) = self._PIVOT(new_B, A, b, c, obj, new_B.index(mb), i)

        return (new_B, A[:, 0:self.var], b)

    # 算法入口
    def Simplex(self, A, b, c):
        B = ''
        (B, A, b) = self.InitializeSimplex(A, b)

        # 函数目标值
        obj = np.dot(c[B], b)

        c = np.dot(c[B].reshape(1, -1), A) - c
        c = c[0]

        # entering basis
        e = np.argmax(c)
        # 找到最大的检验数，如果大于0，则目标函数可以优化
        while c[e] > 0:
            theta = []
            for i in range(len(b)):
                if A[i][e] > 0:
                    theta.append(b[i] / A[i][e])
                else:
                    theta.append(float("inf"))

            l = np.argmin(np.array(theta))

            if theta[l] == float('inf'):
                print("unbounded")
                return False

            (B, A, b, c, obj) = self._PIVOT(B, A, b, c, obj, l, e)

            e = np.argmax(c)

        x = self._CalculateX(B, A, b, c)
        return (x, obj)

    # 得到完整解
    def _CalculateX(self, B, A, b, c):

        x = np.zeros(self.var, dtype=float)
        x[B] = b
        return x

    # 基变换
    def _PIVOT(self, B, A, b, c, z, l, e):
        # main element is a_le
        # l represents leaving basis
        # e represents entering basis

        main_elem = A[l][e]
        # scaling the l-th line
        A[l] = A[l] / main_elem
        b[l] = b[l] / main_elem

        # change e-th column to unit array
        for i in range(self.row):
            if i != l:
                b[i] = b[i] - A[i][e] * b[l]
                A[i] = A[i] - A[i][e] * A[l]

        # update objective value
        z -= b[l] * c[e]

        c = c - c[e] * A[l]

        # change the basis
        B[l] = e

        return (B, A, b, c, z)


s = Simplex()
s.solve()

运行结果

x_1 = 0.000000,x_2 = 0.000000,x_3 = 2.000000
objective value is : 2.000000
------------------------------

B、python包求解

导入相关的包

import numpy as np
from scipy import optimize as op

给出变量取值范围

x1=(0,None)
x2=(0,None)
x3=(0,None)

定义给出变量，确定c,A_ub,B_ub,A_eq,B_eq

c = np.array([2,1,1])# 目标函数系数,3x1列向量
A_ub = np.array([[0,2,-1],[0,1,-1]]) # 不等式约束系数A，2x3维矩阵
B_ub = np.array([-2,1])# 等式约束系数B, 2x1维列向量
A_eq = np.array([[1,-1,1]])# 等式约束系数Aeq，3x1维列向量
B_eq = np.array([2])# 等式约束系数beq，1x1数值

调用函数进行求解

res=op.linprog(c,A_ub,B_ub,A_eq,B_eq,bounds=(x1,x2,x3))#调用函数进行求解
res

运行结果

     con: array([3.41131567e-11])
     fun: 1.9999999999762486
 message: 'Optimization terminated successfully.'
     nit: 4
   slack: array([-3.94368982e-11,  3.00000000e+00])
  status: 0
 success: True
       x: array([2.85788562e-13, 5.03801677e-12, 2.00000000e+00])

第二行的 fun: 1.9999999999762486表示最大值为2；
最后一行的x: array([2.85788562e-13, 5.03801677e-12, 2.00000000e+00])表示x1=0,x2=0,x3=2。

（3）结果对比

通过使用大M法的excel求解、python编程求解和python包求解这三种方法，发现算出来的结果都是x1=x2=0,x3=2,max=2。发现调用python的scipy库算出的结果精度会高一些。

二、非线性规划

1、非线性规划概念

非线性规划是一种求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。运筹学的一个重要分支。20世纪50年代初，库哈(H.W.Kuhn) 和托克 (A.W.Tucker) 提出了非线性规划的基本定理，为非线性规划奠定了理论基础。这一方法在工业、交通运输、经济管理和军事等方面有广泛的应用，特别是在“最优设计”方面，它提供了数学基础和计算方法，因此有重要的实用价值。

2、拉格朗日乘数法

（1）概念

在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。此方法的证明牵涉到偏微分，全微分或链法，从而找到能让设出的隐函数的微分为零的未知数的值。

（2）主要的计算过程

1.假设需要求极值的目标函数(objective function)为f(x,y)，限制条件为φ(x,y)=M

2.设g(x,y)=M-φ(x,y)

3.定义一个新函数

4.用偏导数方法列出方程：

5.求出上述导数=0时，x,y,λ的值，代入即可得到目标函数的极值。

（3）KKT条件

KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法，不同之处在于应用的情形不同。

（4）例题

3、手工数学推导完成上面的例题

当 a = b = c = 1时
Vmax= 1.5396007
x = y = z = 0.5773503

4、利用python求解上述题目

（1）程序代码

from scipy.optimize import minimize
import numpy as np
e = 1e-10 # 非常接近0的值
fun = lambda x : 8 * (x[0] * x[1] * x[2]) # 约束函数f(x,y,z) =8 *x*y*z
cons = ({'type': 'eq', 'fun': lambda x: x[0]**2+ x[1]**2+ x[2]**2 - 1}, # x^2 + y^2 + z^2=1
        {'type': 'ineq', 'fun': lambda x: x[0] - e}, # x>=e，即 x > 0
        {'type': 'ineq', 'fun': lambda x: x[1] - e},
        {'type': 'ineq', 'fun': lambda x: x[2] - e}
       )
x0 = np.array((1.0, 1.0, 1.0)) # 设置初始值
res = minimize(fun, x0, method='SLSQP', constraints=cons)
print('最大值：',res.fun)
print('最优解：',res.x)
print('迭代终止是否成功：', res.success)
print('迭代终止原因：', res.message)

（2）运行结果

最大值： 1.5396007243645415
最优解： [0.57735022 0.57735022 0.57735038]
迭代终止是否成功： True
迭代终止原因： Optimization terminated successfully.

参考文献：
链接: link，线性规划（一）：基本概念；
链接: link，单纯形法 百度百科；
链接: link，大M法（Big M Method）；
链接: link，拉格朗日乘子法。