机器学习西瓜书复习 - 4 SVM（支持向量机）分类

A 说明

svm的内容比较多，再加之中间数度拖延，一直不愿意来写这个博客，本着自己越不爱干的事便越要干的原则，今天终于静下心来写这篇博客。

A.1 目录

• 线性支持向量机：这里主要列出将svm用于分类的基本思路，主要形式是找出分隔线将平面上的样本分开。
• 线性支持向量机求解：这里主要列出利用拉格朗日、对偶优化、SMO算法等进行svm参数估计的一些方法
• 核方法：核方法原本是不打算写的，因为这次复习我也没有时间去手写svm的代码了。但是这个概念很重要，在这里还是要列一下。此外，这里还叙述了一些关于软间隔的知识点
• 简单使用：使用sklearn的svm方法对离职员工分析的一个小实例

B 线性支持向量机

原本复习的风格不应该有太多的图，这样，此时辛辛苦苦构思出来的文字，不会在彼时被图片所掩盖。但是svm比较特殊，对于像我这样几何不太好的人，一张图能传达很多意会的意图，这里还是放上一张简单的草图。

B.1 基本概念

先抛出问题，如下图所示，空间内存在两类样本，分别由方形和星形表示，现在用两条线将两类样本区分开，显然，与红线距离更近的是方形样本，与蓝线更近的是星形样本。同时，从svm的角度来看，这两条线是样本空间的分隔线，线上的样本被称之为支持向量，寻找这样的分隔线用以分类样本的方法，称之为支持向量机。

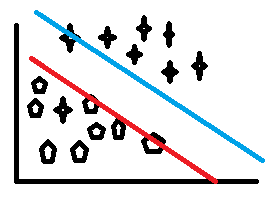
从自然语言的角度来逐个梳理一些上述的概念

• 样本：X，这里，X有两个属性，分别对应x, y坐标轴
• 分隔线：能将样本区分开的直线，即上图的蓝线、红线
• 支持：为了达到最好的分类效果，一个直观的思路便是扩大类间距离，缩小类内距离。这里采用的是扩大类间距离的思路，即满足分隔线分类效果的前提下，让分割线直接的距离尽可能的大，距离达到一个临界点时，两类样本像是被分隔线支撑住的不安分的细胞，这样就引出了支持（support）的概念
• 支持向量：分隔线上的一些样本，这里指的是蓝线上的一个星形样本以及红线上的三个方形样本
• 分类：svm是判别式方法，因此分类的过程是给定一个样本，判断样本所属类别。很显然，如果样本离星形支持向量距离更近，则样本更可能是星形类别，对方形类别亦然。

B.2 基本模型

从分类的过程上来看，除支持向量以外的样本没有直接参与判别过程，因此，svm的训练过程即是求得支持向量的过程。更具体的说，我们需要寻找分隔线，满足

• 分隔线能将样本分开
• 分隔线间距最大

故定义分隔线方程如下：

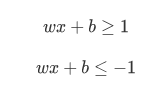
其中上式表示星形类别，下式表示方形类别，取等号时，即为分隔线方程。此时样本已能分开，接下来，要求间隔最大，即

将上述概念整理一下，便可得svm的问题即求解w，使得：

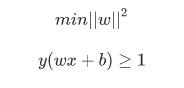
这里有几点需要注意一下
1 将求最大值的问题转化成了求最小值，形式上更加简单
2 式中y为样本类别，从这里也可以看出之前的公式对y取值为-1和1的原因了，两个条件很简单地合并成了一个
3 这个距离公式尽管之前推导了一遍，但是几何不太好的我再看还是不直观，其实做一条垂线，再根据初等几何三角形相关的计算规则去算一下就很明显了，因为结果是正确的，故不列出推导过程，以便下次复习再次推导。

C 线性支持向量机求解

C.1 拉格朗日乘子法

为了更好地理解线性支持向量机求解过程，这里再化一个图，用于解释凸优化过程中的一些概念。
从svm的目标函数来看，这是一个凸优化问题，关于凸函数的一些概念和特点，前面的文章已经有论述，这里明白有这么回事就行了，不进行更详细的叙述了。

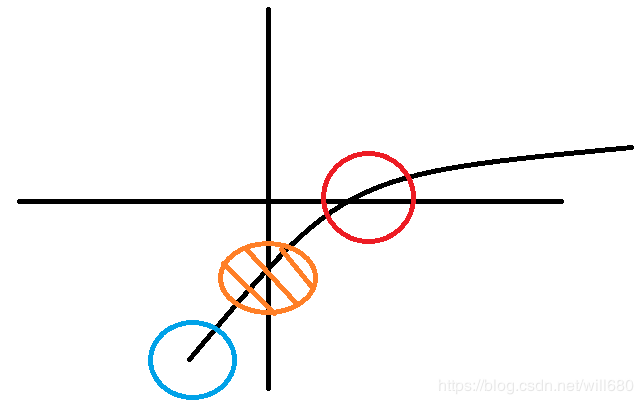
拉格朗日乘子法在这里使用的目的是将包含约束条件的问题转化为没有约束条件的问题
第一步，先列出基本形式

第二步，上图画出了约束函数与目标函数的几种情况

讨论之前，先列出一个事实：一元函数曲线的梯度的方向，是其法向量的方向，证明的思路不太直观，从自然语言的角度来看
1 考虑一元隐函数 F(x,y), 其梯度比较直观，是Fy/Fx
2 根据一元隐函数定理: dy/dx = -Fx/Fy
3 根据法向量的定义，即可得二者方向一致

• 先考虑橙色的圈，即基本形式第二式，可拆解为两部分，g < 0 以及g = 0,。很明显，对于f真正起约束作用的是 g = 0 的部分。因此，可以认为
  
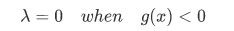
• 对于 g = 0 的情况，此时又可以分为红圈和篮圈两种情况。这两种情况下，求解最小值的过程中，一方面沿着f进行梯度下降，另一方面沿着g进行梯度下降，两条线路会在交叉点达到一个极值的状态。此时，二者的梯度可能是相同的，也可能是相反的，但是肯定是在一条直线上的。具体过程将图中各个点的梯度画出来，便会很明显，为了下次复习不漏掉这部分，这里不再在图中标明梯度
• 再回到基本形式的第二式中，其 g = 0 的情况，应该满足红圈的条件，故达到极值点时，目标函数 f 和约束函数 g 的梯度方向相反。此时有
  
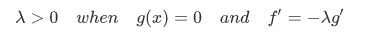
  第三步，将原始的问题转化为没有约束条件的问题：L(x)
  至此，利用拉格朗日法消除约束条件的目的已经达成，其实，将上述的条件调整一下格式，就能得到一系列被称之为KKT条件的式子，本着尽量减少公式和图的复习原则，此处不再叙述。

C.2 对偶问题

关于对偶问题，我很喜欢一个很直白的解释，一个人住10楼，他想知道他离9楼的距离是多少，这是原始问题。这个原始问题很难求解，他没法隔着地板量到楼下，于是他让9楼的人量9楼到天花板的距离，这是对偶问题。这里因为隔着地板，对偶问题的解其实比原始问题要小，是其一个下界，但是相比无法求解的原始问题，已经足够让人满意了。

西瓜书里讲述对偶问题时，很直白，即先对 L(x) 求导取0，得出w的表达式，消去w。再利用SMO对其他的参数进行估算。这实际上是

但是直观上来看，求解过程应该是这样的
先来看max L(x,w,…), 从L(x)的定义来看，已知

则很明显，L(x) 是 f(x)的一个下界，因此，对于 f(x)以外的部分，应该估算其相关的参数来求解其max值
再来看由 minmax 转化为 maxmin的过程：

• 一开始从直观上去理解这一过程，我是从上面的图像进行观察的，得出的结论是二者相等。这是因为我思考的前提是KKT条件已经满足，此时二者等价，这也是svm的对偶问题达到强对偶状态的一个常见条件。
• 其实从公式上推导这一过程也很直观，但是吧（或许是我的错觉），我觉得既然已经得出这一一个美妙又自然的结论了，其中公式推理的过程似乎可有可无，甚至有点绕，所以我选择从自然语言的角度来叙述一些我的个人理解。
• 求解目标函数一定是以满足约束条件为前提的，如果执行min操作，此后约束条件的范围可能被限制了，再进行max操作时，可能会错过约束条件范围内所能达到的最佳值的点。
• 公式推理留待下一次复习的时候再进行

C.3 SMO算法

先给出消除w之后，需要进行max优化的目标函数

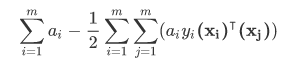
smo算法的基本思路是固定住其他参数，一次求解一个参数，这种方法在 E-M算法，变分推断 中经常被用到，不知道哪个方法是开了先河。但是由于约束条件，这里要特殊一点，一旦其他参数固定了，剩下的参数的值也固定了，因此，这里一次求解两个参数。
求解过程与其他的参数估计没有很大的区别，只是这里有一些需要额外注意的地方

• 选取的第一个参数，应该尽量偏离KKT条件
• 选取的第二个参数，距离第一个应该尽量远

因为之前用代码实现过了svm算法，很繁琐，故再次实现svm算法留待下一次复习。从而对于这两个问题，只能提出一些直观上的个人理解，而无法验证。一个一个来叙述

• 从L(x)的公式来看，需要优化的目标由两部分组成，f , g ，若KKT条件满足，对偶问题满足强对偶条件，梯度下降仅在 f 上进行，反之，梯度下降将在两部分同时进行，故而，直观上来看，收敛会快一些
• 对第二个问题，先考虑反面情况，如果两个参数距离足够近时，此时两个参数对应的样本也足够接近。原本SMO算法一次更新操作能对两个参数进行更新，现在相当于对一个参数进行了更新。从而，二者距离过小时，显然整体梯度变化的总量也会变小。

D 核方法

此处将核方法和软间隔放在一起论述，一方面，是因为核方法引入的高维度空间，可能引起过拟合的情况，而软间隔则用于缓解这一问题。另一方面，个人认为实际应用svm算法的过程中，核的选取和软间隔的配置是两个值得重点关注的方面

D.1 核方法

D.1.1 基本概念

记得第一次接触SVM算法的时候，到知乎找了下思路，顺便提一句，对于从能量的角度来理解交叉熵这样类似的想法也是从知乎的答案中得到的想法，但是并没有引用，尽管是复习博客，但是这个习惯也该改改了，不尊重原作者。从下篇博客开始，一切引用到的资料都应该记录下来
言归正传，杨过与一群赌徒打赌，要一次性把散乱分布着的黑豆黄豆分开，杨大侠一阵狂笑，黑豆黄豆顿时腾空而起，不等第一颗豆子落下，独臂男子已抽出长剑，横向一挥，一股劲风便吹得四周的赌徒脸颊生疼，急忙躲避，待笑声止住，剑风亦止住，围观的赌徒们一个个捂着脸颊难以置信的看着桌上的黑豆还好好的躺着，而黄豆却一个不落地洒在了一柄黑溜溜的巨剑上
桌子上的豆子象征着两个类别的样本，样本之间无法用直线分开，即上述的线性支持向量机无法很好地使用。杨过用内力将豆子逼空，实际上是将样本投影到了一个更高维度的空间，将样本区分开来。这个将样本投影到更高维度的空间使其可分的方法，可称之为核方法
核方法的投影方式与之前讨论过的逻辑回归很像，将原本公式里的 x 用替换为一个函数 φ(x)，同时 x 本身亦是一种核，即 φ(x) = x

D.1.2 核函数

关于核函数的选取，以及不同核函数的对比，因为没时间重写一遍SVM的代码，因此留待下次复习的时候再弄，我有预感，我很快会回到这个部分来

先列出基本的式子

直观上来看，1式即是线性支持向量机的一种扩展形式，但是由于投影到高维空间以后，这个式子中的內积部分计算量很大，因此需要有一种高效的方法进行替代。这个方法称之为核技巧，即2式，一旦选定了 k ,基于核函数的支持向量机跟线性支持向量机的求解便没有多大分别了
再来看这个 k ，西瓜书上给出了几种可供参考的k， sklearn同样给出了几种可选的 k ，并且给出了各种 k 的应用范围。 同时，sklearn还提供了一种指定 k 的方式，即提供一个矩阵，因为k(xi,xj)本质上就是一个矩阵，至于这个矩阵的特点，时间有限来不及写代码进行实践，现在搞清楚了也未必记得住，这次暂时不深究了。
这里暂时明白两个点，一是核方法将当前空间难分的样本投影到更高维度的空间，寻找其可分的间隔面，以及支持向量。二是为了更加有效的运算，使用核技巧，用核函数提供的矩阵来替代高维空间上的內积运算

D.2 软间隔

D.2.1 基本概念

依然仅考虑低维空间：

• 从概念来看，软间隔很好理解，分隔线能在一定范围内浮动，相当于把分隔线加粗了
• 从分类的效果上来说，即是允许一些不满足约束条件的支持向量的存在，此时在引入软间隔之前的模型上分类为A的一些样本，可能会分类为B
• 从定义上来讲，一方面，软间隔允许一些样本不满足约束条件，这些样本我给个简称：异常向量，另一方面，要求这些异常向量的数量尽可能的少
• 从目标函数直观地来看，此处采用hinge损失
  
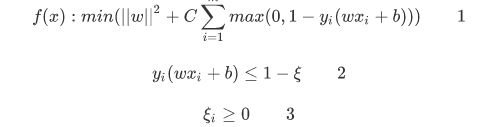
  从2式子来看，右侧小于1时，看做一个比原模型间隔更小的硬间隔支持向量机，软件隔的目标函数的值实际上介于两个硬间隔支持向量机之间。再看1式，由于hinge损失的形式，对于原硬间隔模型，其支持向量依然是软间隔的支持向量。同时，对于缩小的硬间隔模型，其支持向量依然是软间隔的支持向量，于是支持向量变多了，如果将支持向量作为一种引力来理解，那么软间隔依然是基于支持向量的方法，并且稀释了原支持向量的引力，让模型泛化能力更强

D.2.2 计算方法

从上面列出的基本公式来看，软间隔的目标函数可以做出如下的变形

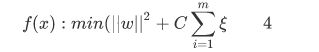
因此，问题又变成了一个有约束条件的凸优化，求解思路与普通的SVM计算方法差不多，这里不再阐述一遍了，在草稿纸上推算还蛮舒服的，再堆到博客上来，很折磨人。老规矩，等下次复习的时候，再补充吧

E 简单使用：离职人员预测

E.1 数据处理

这个任务是kaggle上面的一个简单的分类任务，给定真实的数据集，包含14999个样本，每个样本均有10个特征，描述了一个公司里的员工的一些基本情况和是否在职的状态，数据下载链接如下：
离职人员预测数据集
也不知道是不是这份数据集经过了处理，对数据的各个特征画一下箱图，发现这份数据集没有什么异常值，也没有缺失值，故而，仅仅做了一个简单的缩放处理，便拿来训练模型了

E.2 sklearn代码

这里用了两个svm分类器，一个是基础的分类器，另一个是针对类别不平衡的问题，根据正负样本比例修改了一下class_weight的参数。两个分类器独立进行训练，预测时，对于第一个分类器判定为FF的情况，即原本为离职，却判定为了在职的情况，再放入第二个分类器判定。

# baseline: basic svm
from sklearn import svm
clf1 = svm.SVC(random_state=7,cache_size=1000)
clf1.fit(X_train, y_train)
clf4 = svm.SVC(random_state=7,cache_size=1000,class_weight={1: 4})
clf4.fit(X_train, y_train)

样本中测试集所占比例为0.2，测试结果如下：

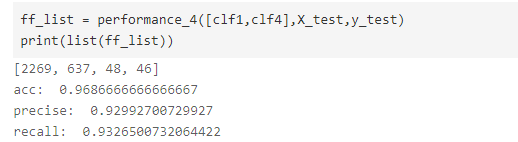
这原本是准备当做一个参照的模型，没有进行任何调参，也没有做什么其他的设计，但是数据的结果还不错，所以svm的这次复习到此为止了。
时间有限，尽管支持向量机的数学证明很优美，但是耗时太多，支持向量回归暂时跳过了，留待下次复习再弄，接下来的复习任务，应该是集成学习了

关于一元函数的梯度方向与法向量一致的证明，参考了
切线、法线、梯度之间的关系https://blog.csdn.net/Queen0911/article/details/100611797