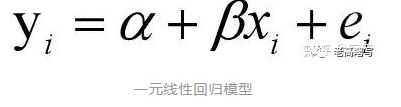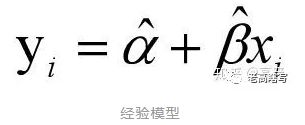Python实现最小二乘法的详细步骤
Python实现最小二乘法的详细步骤
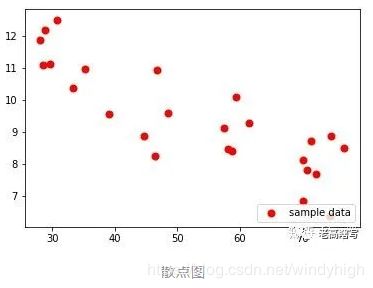
- 画散点图
- 回归模型的参数估计
- 经验模型的效果
- 高老师的公众号
上一篇文章讲了最小二乘算法的原理。这篇文章通过一个简单的例子来看如何通过Python实现最小乘法的线性回归模型的参数估计。
王松桂老师《线性统计模型——线性回归与方差分析》一书中例3.1.3。
说的是一个实验容器靠蒸汽供应热量，使其保持恒温，通过一段时间观测，得到下图表中的这样一组数据：
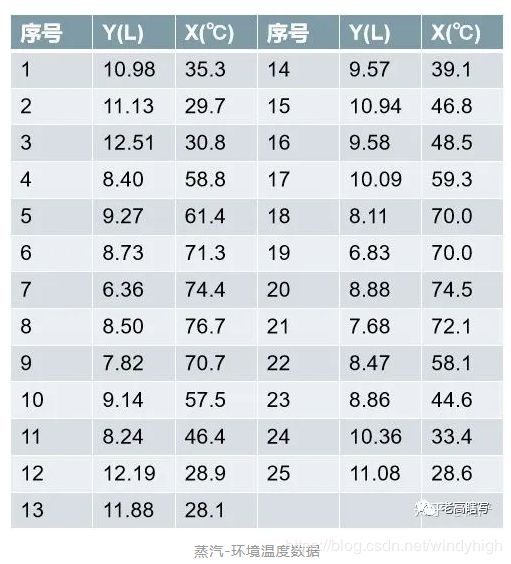
其中，自变量X表示容器周围空气单位时间的平均温度（℃），Y表示单位时间内消耗的蒸汽量（L），共观测了25个单位时间（表中序号一列）。
那么，我们要怎样对这组数据进行线性回归分析呢？一般分三步：（1）画散点图，找模型；（2）进行回归模型的参数估计；（3）检验前面分析得到的经验模型是否合适。
画散点图
创建一个DataTemp的文件夹，在其中分别创建"data"、"demo"文件夹用于存放数据文件、Python程序文件。
把前面图中的数据导入Excel中，命名为：“蒸汽供应.xlsx”，用来作为数据源。
创建Python文件：”leastsquare.py“。在文件头加入utf-8编码的说明以支持中文字符，然后添加必要的注释。
# -*- coding: utf-8 -*-
"""
Created on Fri Mar 20 14:07:41 2020
@author: gao
"""
import必要的第三方库。
"""
第三方库
"""
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
import numpy as np
使用下面的代码将Excel数据读入Python Pandas DataFrame中。
"""
把excel中的数据读入datafram
"""
filePath = u'../data/蒸汽供应.xlsx' #含中文字符，前面加u表示用Unicode 格式进行编码
data = pd.read_excel(filePath, index_col=u'序号')
提取其中的Y、X列并绘制散点图
Xi = data[u'X']
Yi = data[u'Y']
"""
画散点图
"""
plt.figure()
plt.scatter(Xi, Yi, color='red', label='sample data',linewidth=2)
plt.legend(loc='lower right')
plt.show()
散点图结果如下：
从图中看出大致服从一个线性分布，所以我们采用一元线性回归模型来进行分析。
回归模型的参数估计
一元线性模型的一般公式为
我们使用最小二乘法估算出α、β即可求出经验回归方程。
Python中对一元线性模型的参数进行参数估计是很简单的，如下代码所示：
def fun(p,x): #回归模型函数
k,b = p
return k*x+b
def error(p,x,y): #误差
return fun(p,x)-y
p0 = np.array([1,3])
para = leastsq(error,p0,args=(Xi,Yi))
k,b = para[0]
上面代码的关键之处有三点：
- 定义模型函数、误差函数。其中误差函数error，实际上就是我们模型的估计值与实际的观察值之差，我们就是通过这个差值的最小二乘来对模型中的参数进行估计的。也就是说，前面的经验模型的参数取不同的值，那对于xi可以求出不同的yi，这个yi是我们估计值和实际的观测值进行求差就是估计误差，参数取值不同估计误差不同，我们要找到一组参数使得对于所有的观测值的误差的平方和最小。
- 调用scipy的leastsq函数时，需要有误差函数、初始参数作为输入，还需要把我们读到的观测数据作为参数传入leastsq函数，这是此函数的三个关键的输入参数。
- leastsq的返回参数是多个，所以放到一个元组（tuple）中，返回tuple类型para的第一个元素para[0]是一个nupy.ndarray类型，存放的即是满足最小二乘规则的估计参数。
经验模型的效果
可以使用下面的代码打印经过最小二乘运算后的经验模型。
"""
打印结果
"""
print('y='+str(round(k,2)) + 'x+' +str(round(b,2)))
最后一步工作就是把我们的经验模型的线画到前面的散点图上，看一下模型的效果。
"""
绘制结果曲线
"""
x=np.linspace(20,80,2)
y=k*x+b
"""
画散点图
"""
plt.figure()
plt.scatter(Xi, Yi, color='red', label='sample data',linewidth=2)
plt.plot(x,y,color='blue',label='result line')
plt.legend(loc='lower right')
plt.show()
绘出的结果图像如下：
当然，我们还可以通过判定系数来看一下我们的回归方程与数据拟合的效果好坏，这个在后续的文章中再说。