应用机器学习（二）：k-NN 分类器

分类问题

在统计和机器学习里，分类问题的目标是：取一个新的观测向量 x ，将它分到 K 个离散的类 Ck ( k=1,2,…,K ) 之一。一般来说，类之间是互不相容的，因此，每一个观测只能被分到一个类中。举一个分类问题的例子：

例子：垃圾邮件的过滤

人们在日常email的处理中，总能不可避免地收到垃圾邮件。怎样从一批邮件中区别哪些是正常邮件，哪些是无用的垃圾邮件呢？这就是一个两类的分类问题，即，对收到的一个邮件，将它分到正常邮件类或者垃圾邮件类。那么，按照什么原则分类呢？可以考虑邮件的内容、文本模式、寄件人地址等，这些称为特征。根据这些特征来对邮件是否为垃圾邮件进行分类，分类的结果可能是这样的：

在机器学习里，分类( classification )是一种有监督学习（supervised learning )的方法。通常，将数据分成训练集（Training set）、验证集（Validation set）和检验集（Test set）三部分。在训练集上建立统计模型，估计未知参数；在验证集上优化模型，包括调整参数；最后，在检验集上检验该方法的优劣性及执行效率。所谓有监督学习，在分类问题里，指的是训练集的观测对象的类别标签（class labels）是已知的，即，已知对象的所属类别。

频率学派与贝叶斯学派的“分类”

早期的分类问题由频率学派的代表人物，著名统计学家 Fisher 提出，并应用于两类的分类问题。Fisher 假设每个类对应特定的正态总体，并提出了线性判别函数( Fisher’s linear discriminant function )作为观测对象的分类准则。

与频率学派的分类思想不同，贝叶斯( Bayesian )学派的分类，既考虑了不同类的总体，同时，也考虑不同总体出现的先验概率和错分类造成的损失，提出用损失函数 ( Loss of function ) 度量损失。

线性分类器

设输入向量为 x ，权向量 w ，令 f(x)=wTx ，根据函数 f(x) 的值决定 x 的分类结果，称 f(x) 为线性分类器 ( Linear classifier )。其中，权向量 w 通过对已知类标签的训练样本学习得到。最简单的线性分类器应用于两类的分类问题。给定一个输入向量 x ，若 f(x)≥0 ，则将 x 分类 C1 ，否则，分到类 C2 。

分类算法

常见的分类算法有：

• 基于实例的方法

  • k-近邻

• 基于概率的方法

  • Naive Bayes 分类器

  • Logistic 回归

• 线性模型

  • 支持向量机

• 决策模型

  • 决策树
  • 随机森林

K -近邻

K-近邻( k-nearest neighbors / knn )是一类基于实例 ( instance-based ) 的非参数学习算法。在这里，输入是由数据集里的 k 个最近的训练实例组成，输出是一个类成员。一个新对象的分类原则是，它被分到离它最近的 k 个邻居中的多数所在的那个类中。特别地，k = 1 时，该对象被分到离它最近的邻居所在的类中。通常，可以赋邻居权值表示邻居对分类的贡献。例如，可以取对象到每个邻居的距离的倒数作为它的权值。knn 算法的缺点是，它对数据的局部结构敏感，容易过度拟合数据。

K-近邻分类器

设一个分类问题，类集 V={C1,C2,…,Cs} 。 待分类的观测点 (x,y) ， x∈Rd ， y 是观测 x 的类标签， y∈V 未知。设已知类标签的训练样本 {(xi,yi)∈Rd×V,i=1,2,…,n} 。定义 Rd 上的距离测度：

对于连续变量，一般采用欧氏距离。对于离散变量，例如，文本分类问题，可以采用重叠度量( overlap metric )；在基因表达微阵列数据分析中，也可以用 Pearson 或 Spearman 相关系数。

计算训练样本与 x 的距离，按距离的升序排序训练样本为 (x(i),y(i)),i=1,2,…,n ，此时， ||x(1)−x||≤⋯≤||x(n)−x|| . 那么， x 的类标签

y=argmaxv∈V∑i=1kδ(v,y(i))

这里，函数 δ(a,b)=1 ，当 a=b 时；否则， δ(a,b)=0 . 此即，将 x 分到离它最近的 k 个邻居里的大多数所在的类中。

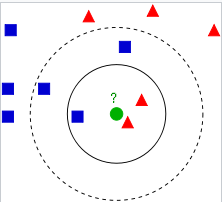
下面举一个 k-NN 分类的简单例子，如图3所示。待分类的样本(绿圈)
要被分到蓝色方块类或红色三角类。如果 k=3 ，绿圈将被分到蓝色方块类，因为离它最近的3个邻居里，有两个在方块类；如果 k=5 ，同样的道理，绿圈将被分到三角类。

k-NN 是依据服从“大多数”的分类原则，这样容易引起过度拟合数据的问题。克服过度拟合的常见方法是，根据 k 个近邻与观测点的距离，赋给更近的邻居以更大的权值，彰显它们对分类的贡献。通常，权值取距离的倒数， ωi=1/d2(x,x(i)),i=1,2,…,k , 然后再归一化。此时，分类为

y=argmaxv∈V∑i=1kωiδ(v,y(i))

参数 k 的选择

k 的选择依赖于数据。通常，选择较大的k，能够减少分类的噪声水平，但使分类的边界更模糊，这样会影响处于边界的样本的分类准确性。为了选择最优的k，可以使用验证数据的办法。首先，将数据分成独立的训练集和验证集两部分。然后，在训练集上，用不同的k值训练 k-NN 分类器；在验证集上，检验不同的 k 的分类效果，选择最佳的k。

k-NN 对于输入特征的值域比较敏感，如果引入无关的特征甚至会大大降低分类准确性。可行的校正办法是，将数据归一化到[0, 1]或[-1, 1]的区间内；或者，标准化数据 x←x−μ^σ^ ,其中， μ^,σ^ 分别是样本均值和样本标准差。

对于两类的分类问题，最好取k 为奇数，因为如果k 为偶数，可能 k 个近邻里处于两类的邻居数都是 k/2 ，这种相等的情况称为“结”(tie )。这种情况下，可以采用 bootstrap 重抽样的办法选择经验最优的 k 。

数据试验

我们在著名的鸢尾花 ( Iris flower )数据集( 也称 Fisher’s Iris 数据集，或 Anderson’s Iris 数据集 )作 knn 分类。该数据集测量了鸢尾花的三个品种，Iris setosa, versicolor, and virginica，每个品种的萼片(sepals )长度和宽度、花瓣(petals )的长度和宽度 (单位：厘米) ，这些数据量化三个鸢尾花品种在形态上的差异。

鸢尾花数据集包括三个品种各50个样本，共150个样本；5个特征，即，Sepal length, Sepal width, Petal legth, Petal width and Species 的测量值。在 R 的 datasets 包中分别以数据框 iris 和数组iris3 表示。下面显示数据框 iris 的前6行。

head(iris)

现在，将数组 iris3 每个品种的前25个样本组成训练集，后25个样本组成检验集，在训练集上构建 k-NN 分类器，在检验集上检验分类效果。这是一个有监督学习，使用 R 包 class 的函数 knn 完成。

# 加载包class
library(class)    
# 去掉变量Species
iris_data <- iris[, -5]
# 标准化变量(列)
iris_data <- scale(iris_data)
# 提取三个品种的前25个样本组成训练集
train <- iris_data[c(1:25, 51:75, 101:125),]
train_labels <- iris[c(1:25, 51:75, 101:125), 5]
# 提取三个品种的后25个样本组成检验集
test <- iris_data[c(26:50, 76:100, 126:150),]
test_labels <-iris[c(26:50, 76:100, 126:150), 5] 
# 在训练集上建立knn分类器，在检验集上预测分类结果
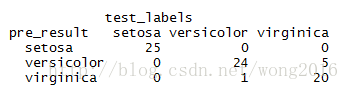
pre_result <- knn(train, test, train_labels, k = 3, prob=TRUE)

最后，将预测结果和检验标签作比较。

table(pre_result, test_labels)