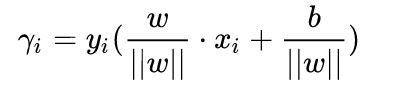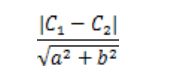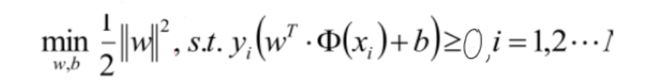数据挖掘十大算法（六）------SVM算法

SVM算法（support vector machines，支持向量机）

（一）、算法核心思想

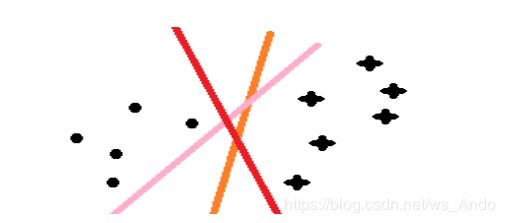
SVM算法最初是为二值分类问题涉及的，是一个二分类的分类模型（分类器），当处理多分类问题时，需要我们构造合适的多类分类器。这里以最简单的二分类问题来记录。给定一个包含正例、反例的样本集合，SVM的目的是寻找一个超平面分割线（在二维中实质就是一条线，三维中就是一个平面）来对样本进行分割。

 例如上图，我们有三条直线可以将样本划分，但是哪一个划分是最好的？这就是SVM所要研究解决的问题。

设一条直线 G(x) = W * X + b = 0 为最优的分割线（超平面），将样本分为两类，我们的任务就是怎样获得最优直线并求得 W 和 b 的值，在 SVM 中就是支持向量和超平面最小距离的最大值（距离超平面最近的点 有最远的距离，就是最优的超平面）；

注：SVM的二分类特别重要，在超平面 W * X + b = 0 确定的情况下，|W * X + b| 可以相对地表示 X 距离超平面的远近。对于二分类问题 如果 W * X + b > 0 ，则 x 的类型划分为 1 ，W * X + b < 0 则 x 的类型划分为 -1。则我们可以用 y(W * X + b ) >= 0 表示 x 的划分结果正确， y(W * X + b ) < 0 表示 x 的划分结果错误。且 y(W * X + b ) 的值越大，分类结果的确信度越大。

由上述的式子我们可以定义样本点（xi , yi）与超平面（w ,b ）之间的函数间隔（几何间隔）定义为 ：

 我们观察会发现，如果 w ,b 同时放大或缩小 N 倍， 超平面 G(x) = NW * NX + b 不变，但是点与超平面的函数间隔改变了 N 倍。所以，为了解决这个问题，我们将 w 的大小固定，列如 ||w|| = 1 ，这样无论w ,b 怎么变， 超平面和函数间隔都不会改变。

所以再次改写函数间隔（几何间隔）：

 总结一下：在二维空间中，几何间隔就是点到超平面的距离（点到直线的距离），；在三维即以上的空间中，就是点到超平面的距离。

（二）、超平面的选择

关键核心点：支持向量和超平面最小距离的最大值（距离超平面最近的点 有最远的距离，就是最优的超平面）

①、距离超平面最近的点

r = min {r1 , r2 ,r3 ,......ri}，在求得所有几何间隔中取最小值。

②、最近的点有最远的距离

max(w,b) {r}

总结一下： 红色部分就是求得最近的点， max部分就是求得最近的点有最远距离。

 现在知道了问题的关键所在，我们先来描述距离超平面最近的点，我们需要找到两个和这个超平面平行且距离相等的超平面：

H1: y = wx + b=1 和 H2: y = wx + b=-1，如下图所示：

在这两个超平面上的样本点也就是理论上离分隔超平面最近的点，是它们的存在决定了H1和H2的位置，支撑起了分界线，它们就是所谓的支持向量，这就是支持向量机的由来。

H1: y = wx + b=1 和 H2: y = wx + b=-1 ，两平行直线之间的距离公式：

 带入已知值，得 2 / ||w||，H1,H2两直线的距离为 m = 2 / ||w|| 。

再处理最近的点有最远距离，相当于求 m = 2 / ||w|| 的最大值。相当于最小化 ||w|| 即可。为了之后的求导和计算方便，进一步等价于最小化

 再与之前划分正确的 y(W * X + b ) >= 0式子结合，就成了一个最优化问题：

目标函数：min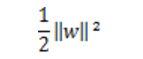，约束条件： y(W * X + b ) >= 0。

 总结步骤：第一步：找两条平行且距离相等的超平面。第二步：求得两直线距离 m = 2 / ||w|| 。第三步：求最近点的最远距离，所以将max{ 2 / ||w|| }  转化成求 min {||w||} ，再为了方便求导，再次转化成求的最小值。第四步：结合之前的划分正确的不等式 y(W * X + b ) >= 0，完成函数求值即可。

SVM算法思想基本完成，后面的任务就是如何求得该式。

构造拉格朗日函数进行求解，由于约束条件中还带有不等式约束，所以还需要考虑KKT条件。（具体求解和不足之处 日后补充修改。）

该博客用于自己记录、学习，便于日后复习，参考学习博客：

https://blog.csdn.net/u012581541/article/details/51181041

https://blog.csdn.net/lisi1129/article/details/70209945?locationNum=8&fps=1