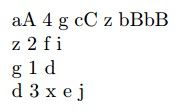多叉树应用（多叉树创建， 遍历）

1. 项目上遇到了一个典型的多叉树应用案例， 记录一下。

（1）

//结构

typedef struct  st_OriTree
{
	int levelValue;    //树的level
	int orderValue;    //排序值
	QString nameValue; //当前节点名称
	QString preNameValue; //前置节点名称
	QMultiMap childrenList; //子节点列表
}OriTree;

（2）

//创建多叉树，要求： 节点不允许重复。在构建的时候， 层次优先遍历树结构，查找重复节点。

void TNDataCache::appendTreeNode(OriTree **head, OriTree node)
{
	if (*head == nullptr)
		return;

	QQueue queue;
	queue.append(*head);

	bool isExist = false;
	OriTree* p = nullptr;
	OriTree* q = *head;
	while (!queue.isEmpty())
	{
		p = queue.front();
		queue.pop_front();
		if (p != nullptr)
		{
			for (int i = 0; i < p->childrenList.count(); i++)
			{
				if (p->childrenList.values().at(i)->preNameValue == node.preNameValue
					&& p->childrenList.values().at(i)->levelValue == node.levelValue)
				{
					if (p->childrenList.values().at(i)->nameValue == node.nameValue)
					{
						isExist = true;
						break;
					}
					continue;
				}
				if (p->childrenList.values().at(i)->levelValue == node.levelValue - 1
					&& p->childrenList.values().at(i)->nameValue == node.preNameValue)
				{
					q = p->childrenList.values().at(i);
				}
				queue.append(p->childrenList.values().at(i));
			}
		}
	}
	if (!isExist && q!= nullptr)
	{
		//create new node
		OriTree * newNode = new OriTree();
		if (newNode == nullptr || p == nullptr)
		{
			qDebug() << "new OriTree node failed , node Name :" << node.nameValue;
			return;
		}
		newNode->feedValue = node.feedValue;
		newNode->levelValue = node.levelValue;
		newNode->nameValue = node.nameValue;
		newNode->orderValue = node.orderValue;
		newNode->preNameValue = node.preNameValue;
		Q_ASSERT(q->feedValue == nullptr);
		if (q->feedValue != nullptr)
		{
			qDebug() << "new OriTree build tree error, node Name" << node.nameValue;
			return;
		}
		q->childrenList.insert(node.orderValue, newNode);
	}
}

（3） 

// 层次优先遍历多叉树结构（利用队列实现），按层，深度输出节点名称。 如果逆向输出，需要借助栈

void travel(OriTree * tree)
{
	if (tree == nullptr)
		return;

	QQueue qTree;
	qTree.append(tree);
	
	OriTree* p = nullptr;
	while (!qTree.isEmpty())
	{
		p = qTree.front();
		qTree.pop_front();
		if (p != nullptr)
		{
			for (int i = 0; i < p->childrenList.count(); i++)
			{
				qDebug() << p->childrenList.values().at(i)->nameValue;
				qTree.append(p->childrenList.values().at(i));
			}
		}
	}
}

（4）

//(递归)深度优先遍历多叉树，输出所有叶子路径, QueuepathQueue ;

void travel(OriTree * tree)
{
	pathQueue.append(tree);
	if (tree == nullptr || tree->childrenList.values().count() == 0)
	{
		//一条路径遍历完毕,此时pathQueue为完整的节点路径
		qDebug() << pathQueue.size();
		//将最后入队的节点pop
		pathQueue.pop_back();
		return;
	}
	for (int i = 0; i < tree->childrenList.values().count(); i++)
	{
		BuildTreeItem(tree->childrenList.values().at(i));
		if (i == tree->childrenList.values().count() - 1)
		{
			pathQueue.pop_back(); //当前节点 pop
		}
	}
}

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

以下内容来自博客： 

http://www.cnblogs.com/unixfy/p/3486179.html

多叉树的设计、建立、层次优先遍历和深度优先遍历

多叉树的设计、建立、层次优先遍历和深度优先遍历

         早起曾实现过一个简单的多叉树《实现一个多叉树》。其实现原理是多叉树中的节点有两个域，分别表示节点名以及一个数组，该数组存储其子节点的地址。实现了一个多叉树建立函数，用于输入格式为A B。A表示节点的名字，B表示节点的子节点个数。建立函数根据用户的输入，首先建立一个新的节点，然后根据B的值进行深度递归调用。用户输入节点的顺序就是按照深度递归的顺序。另外，我们实现了一个层次优先遍历函数。该函数用一个队列实现该多叉树的层次优先遍历。首先将根节点入队列，然后检测队列是否为空，如果不为空，将队列出队列，访问出队列的节点，然后将该节点的子节点指针入队列，依次循环下去，直至队列为空，终止循环，从而完成整个多叉树的层次优先遍历。

         本文我们将还是介绍一个多叉树，其内容和之前的实现差不多。

         首先，用户的多叉树数据存储在一个文件中，格式如下：

每行的第一个元素指定一个节点，其中第一行指定了该多叉树的根节点。第二个元素表示该节点有几个子节点，紧接着后面跟了几个子节点。

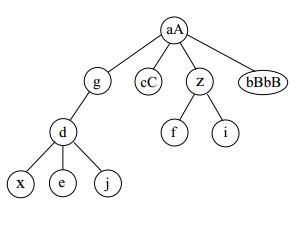
         根据以上数据文件，其对应的多叉树应该是如下：

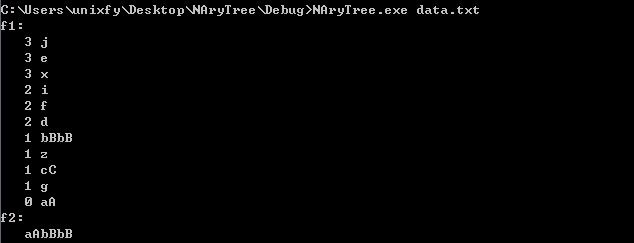
我们想得到结果是将书中的节点按深度进行输出，比如先输出深度最深的节点：x e j，然后输出深度为2的节点：d f i，之后再输出深度为1的节点：g cC z bBbB，最后输出根节点：aA。

         按照深度将节点输出，很显然是用层次优先遍历的方法解决。层次优先遍历的实现原理就是从根节点开始，利用队列实现。

         另外，我们想得到从根节点开始到叶子节点直接所有节点名字加起来最长的一个路径，比如上面的树中存在以下几条路径：

                                                 aA g d x

                                                 aA g d e

                                                 aA g d j

                                                 aA cC

                                                 aA z f

                                                 aA z i

                                                 aA bBbB

显然，在这些路径中，aA bBbB是所有路径上节点名字加起来最长的一个路径。求解从根节点到叶子节点上的所有路径，利用深度优先遍历更为合适。

         下面我们讨论一下多叉树节点应该如何建立。首先多叉树的节点应该如何定义，节点除了有自身的名字外，还要记录其子节点有多少个，每个子节点在哪里，所以我们需要增加一个记录子节点个数的域，还要增加一个数组，用来记录子节点的指针。另外，还要记录多叉树中每个节点的深度值。

         在读取数据文件的过程中，我们顺序扫描整个文件，根据第一个名字，建立新的节点，或者从多叉树中找到已经有的节点地址，将后续的子节点生成，并归属于该父节点，直至扫描完整个数据文件。

         读取完整个文件后，也就建立了多叉树，之后，我们利用队列对多叉树进行广度优先遍历，记录各个节点的深度值。并将其按照深度进行输出。

         获取从根节点到子节点路径上所有节点名字最长的路径，我们利用深度优先遍历，递归调用深度优先遍历函数，找到最长的那个路径。

         初次之外，还需定义队列结构体，这里使用的队列是循环队列，实现相关的队列操作函数。还有定义栈的结构体，实现栈的相关操作函数。另外对几个内存分配函数、字符串拷贝函数、文件打开函数进行了封装。需要注意的一点就是当操作完成后，需要对已经建立的任何东西都要销毁掉，比如中途建立的队列、栈、多叉树等，其中还包含各个结构体中的指针域。

         另外，函数测试是用户在命令行模式下输入程序名字后面紧跟数据文件的形式。

         该程序的主要部分有如下几点：

         1.多叉树节点的定义和生成一个新节点

         2.数据文件的读取以及多叉树的建立

         3.根据节点名字在多叉树中查找节点的位置

         4.多叉树的层次优先遍历

         5.多叉树的深度优先遍历

         6.队列的定义以及相关操作函数实现

         7.栈的定义以及相关操作函数实现

         8.消毁相关已经建立好的队列、栈、多叉树等

         9.测试模块

         下面我们给出相关的程序实现，具体细节可以查看代码和注释说明。

// 多叉树的建立、层次遍历、深度遍历

#include 
#include 
#include 

#define M 100+1 // 宏定义，定义最大名字字母长度

// 定义多叉树的节点结构体
typedef struct node_t
{
    char* name;               // 节点名
    int   n_children;         // 子节点个数
    int   level;              // 记录该节点在多叉树中的层数
    struct node_t** children; // 指向其自身的子节点，children一个数组，该数组中的元素时node_t*指针
} NODE; // 对结构体重命名

// 实现一个栈，用于后续操作
typedef struct stack_t
{
    NODE** array; // array是个数组，其元素为NODE*型指针
    int    index; // 指示栈顶元素
    int    size;  // 栈的大小
} STACK; // 重命名

// 实现一个队列，用于后续操作
typedef struct queue_t
{
    NODE** array; // array是个数组，其内部元素为NODE*型指针
    int    head;  // 队列的头
    int    tail;  // 队列的尾
    int    num;   // 队列中元素的个数
    int    size;  // 队列的大小
} QUEUE;

// 这里的栈和队列，都是用动态数组实现的，另一种实现方式是用链表

// 内存分配函数
void* util_malloc(int size)
{
    void* ptr = malloc(size);

    if (ptr == NULL) // 如果分配失败，则终止程序
    {
        printf("Memory allocation error!\n");
        exit(EXIT_FAILURE);
    }

    // 分配成功，则返回
    return ptr;
}

// 字符串赋值函数
// 对strdup函数的封装，strdup函数直接进行字符串赋值，不用对被赋值指针分配空间
// 比strcpy用起来方便，但其不是标准库里面的函数
// 用strdup函数赋值的指针，在最后也是需要free掉的
char* util_strdup(char* src)
{
    char* dst = strdup(src);

    if (dst == NULL) // 如果赋值失败，则终止程序
    {
        printf ("Memroy allocation error!\n");
        exit(EXIT_FAILURE);
    }

    // 赋值成功，返回
    return dst;
}

// 对fopen函数封装
FILE* util_fopen(char* name, char* access)
{
    FILE* fp = fopen(name, access);

    if (fp == NULL) // 如果打开文件失败，终止程序
    {
        printf("Error opening file %s!\n", name);
        exit(EXIT_FAILURE);
    }

    // 打开成功，返回
    return  fp;
}

// 实现一些栈操作

// 栈的初始化
STACK* STACKinit(int size) // 初始化栈大小为size
{
    STACK* sp;

    sp = (STACK*)util_malloc(sizeof (STACK));
    sp->size  = size;
    sp->index = 0;
    sp->array = (NODE**)util_malloc(size * sizeof (NODE*));

    return sp;
}

// 检测栈是否为空
// 如果为空返回1，否则返回0
int STACKempty(STACK* sp)
{
    if (sp == NULL || sp->index <= 0) // 空
    {
        return 1;
    }
    return 0;
}

// 压栈操作
int STACKpush(STACK* sp, NODE* data)
{
    if (sp == NULL || sp->index >= sp->size) // sp没有被初始化，或者已满
    {
        return 0; // 压栈失败
    }

    sp->array[sp->index++] = data; // 压栈
    return 1;
}

// 弹栈操作
int STACKpop(STACK* sp, NODE** data_ptr)
{
    if (sp == NULL || sp->index <= 0) // sp为初始化，或者为空没有元素
    {
        return 0;
    }

    *data_ptr = sp->array[--sp->index]; // 弹栈
    return 1;
}

// 将栈消毁
void STACKdestroy(STACK* sp)
{
    free(sp->array);
    free(sp);
}
// 以上是栈的操作

// 实现队列的操作
QUEUE* QUEUEinit(int size)
{
    QUEUE* qp;

    qp = (QUEUE*)util_malloc(sizeof (QUEUE));
    qp->size  = size;
    qp->head  = qp->tail = qp->num = 0;
    qp->array = (NODE**)util_malloc(size * sizeof (NODE*));

    return qp;
}

// 入队列
int QUEUEenqueue(QUEUE* qp, NODE* data)
{
    if (qp == NULL || qp->num >= qp->size) // qp未初始化或已满
    {
        return 0; // 入队失败
    }

    qp->array[qp->tail] = data; // 入队，tail一直指向最后一个元素的下一个位置
    qp->tail = (qp->tail + 1) % (qp->size); // 循环队列
    ++qp->num;
    return 1;
}

// 出队列
int QUEUEdequeue(QUEUE* qp, NODE** data_ptr)
{
    if (qp == NULL || qp->num <= 0) // qp未初始化或队列内无元素
    {
        return 0;
    }

    *data_ptr = qp->array[qp->head]; // 出队
    qp->head = (qp->head + 1) % (qp->size); // 循环队列
    --qp->num;

    return 1;
}

// 检测队列是否为空
int QUEUEempty(QUEUE* qp)
{
    if (qp == NULL || qp->num <= 0)
    {
        return 1;
    }

    return 0;
}

// 销毁队列
void QUEUEdestroy(QUEUE* qp)
{
    free(qp->array);
    free(qp);
}
// 以上是队列的有关操作实现

// 生成多叉树节点
NODE* create_node()
{
    NODE* q;

    q = (NODE*)util_malloc(sizeof (NODE));
    q->n_children = 0;
    q->level      = -1;
    q->children   = NULL;

    return q;
}

// 按节点名字查找
NODE* search_node_r(char name[M], NODE* head)
{
    NODE* temp = NULL;
    int i = 0;

    if (head != NULL)
    {
        if (strcmp(name, head->name) == 0) // 如果名字匹配
        {
            temp = head;
        }
        else // 如果不匹配，则查找其子节点
        {
            for (i = 0; i < head->n_children && temp == NULL/*如果temp不为空，则结束查找*/; ++i)
            {
                temp = search_node_r(name, head->children[i]); // 递归查找子节点
            }
        }
    }

    return temp; // 将查找到的节点指针返回，也有可能没有找到，此时temp为NULL
}

// 从文件中读取多叉树数据，并建立多叉树
void read_file(NODE** head, char* filename)
{
    NODE* temp = NULL;
    int i = 0, n = 0;
    char name[M], child[M];
    FILE* fp;

    fp = util_fopen(filename, "r"); // 打开文件

    while (fscanf(fp, "%s %d", name, &n) != EOF) // 先读取节点名字和当前节点的子节点个数
    {
        if (*head == NULL) // 若为空
        {
            temp = *head = create_node();   // 生成一个新节点
            temp->name = util_strdup(name); // 赋名
        }
        else
        {
            temp = search_node_r(name, *head); // 根据name找到节点
            // 这里默认数据文件是正确的，一定可以找到与name匹配的节点
            // 如果不匹配，那么应该忽略本行数据
        }
        // 找到节点后，对子节点进行处理
        temp->n_children = n;
        temp->children   = (NODE**)malloc(n * sizeof (NODE*));
        if (temp->children == NULL) // 分配内存失败
        {
            fprintf(stderr, "Dynamic allocation error!\n");
            exit(EXIT_FAILURE);
        }

        // 如果分配成功，则读取后面的子节点，并保存
        for (i = 0; i < n; ++i)
        {
            fscanf(fp, "%s", child); // 读取子节点
            temp->children[i] = create_node(); // 生成子节点
            temp->children[i]->name = util_strdup(child); // 读子节点赋名
        }
    }

    // 读取完毕，关闭文件
    fclose(fp);
}

// 实现函数1
// 将多叉树中的节点，按照深度进行输出
// 实质上实现的是层次优先遍历
void f1(NODE* head)
{
    NODE* p = NULL;
    QUEUE* q = NULL; // 定义一个队列
    STACK* s = NULL; // 定义一个栈
    int i = 0;

    q = QUEUEinit(100); // 将队列初始化大小为100
    s = STACKinit(100); // 将栈初始化大小为100

    head->level = 0; // 根节点的深度为0
    
    // 将根节点入队列
    QUEUEenqueue(q, head);

    // 对多叉树中的节点的深度值level进行赋值
    // 采用层次优先遍历方法，借助于队列
    while (QUEUEempty(q) == 0) // 如果队列q不为空
    {
        QUEUEdequeue(q, &p); // 出队列
        for (i = 0; i < p->n_children; ++i)
        {
            p->children[i]->level = p->level + 1; // 对子节点深度进行赋值：父节点深度加1
            QUEUEenqueue(q, p->children[i]);      // 将子节点入队列
        }
        STACKpush(s, p); // 将p入栈
    }

    while (STACKempty(s) == 0) // 不为空
    {
        STACKpop(s, &p); // 弹栈
        fprintf(stdout, "   %d %s\n", p->level, p->name);
    }

    QUEUEdestroy(q); // 消毁队列
    STACKdestroy(s); // 消毁栈
}

// 实现函数2
// 找到从根节点到叶子节点路径上节点名字字母个数最大的路径
// 实质上实现的是深度优先遍历
void f2(NODE* head, char* str, char** strBest, int level)
{
    int   i   = 0;
    char* tmp = NULL;

    if (head == NULL)
    {
        return;
    }

    tmp = (char*)util_malloc((strlen(str) + strlen(head->name) + 1/*原程序中未加1*/) * sizeof (char));
    sprintf(tmp, "%s%s", str, head->name);

    if (head->n_children == 0)
    {
        if (*strBest == NULL || strlen(tmp) > strlen(*strBest))
        {
            free(*strBest);
            *strBest = util_strdup(tmp);
        }
    }

    for (i = 0; i < head->n_children; ++i)
    {
        f2(head->children[i], tmp, strBest, level + 1);
    }

    free(tmp);
}

// 消毁树
void free_tree_r(NODE* head)
{
    int i = 0;
    if (head == NULL)
    {
        return;
    }

    for (i = 0; i < head->n_children; ++i)
    {
        free_tree_r(head->children[i]);
    }

    free(head->name);
    // free(head->children); // 消毁子节点指针数组
    free(head);
}


int main(int argc, char* argv[])
{
    NODE* head = NULL;
    char* strBest = NULL;

    if (argc != 2)
    {
        fprintf(stderr, "Missing parameters!\n");
        exit(EXIT_FAILURE);
    }

    read_file(&head, argv[1]);

    fprintf(stdout, "f1:\n");
    f1(head);
    f2(head, "", &strBest, 0);
    fprintf(stdout, "f2:\n   %s\n", strBest);

    free_tree_r(head);

    return EXIT_SUCCESS;
}

其他： https://my.oschina.net/u/1179554/blog/376524

---------------------------------------------------------------------------------------------------------------------------------------------------------

深度优先遍历

 

1．深度优先遍历的递归定义

 

　　假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点)，则深度优先遍历可定义如下：首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。

　　图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索(Depth-First Search)。相应地，用此方法遍历图就很自然地称之为图的深度优先遍历

 

2.基本实现思想：

（1）访问顶点v；

（2）从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；

（3）重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。

 

3.伪代码

递归实现

（1）访问顶点v；visited[v]=1；//算法执行前visited[n]=0

（2）w=顶点v的第一个邻接点；

（3）while（w存在）  

           if（w未被访问）

                   从顶点w出发递归执行该算法； 
           w=顶点v的下一个邻接点；

 

非递归实现

 （1）栈S初始化；visited[n]=0；

 （2）访问顶点v；visited[v]=1；顶点v入栈S

 （3）while(栈S非空)

            x=栈S的顶元素(不出栈)；

            if(存在并找到未被访问的x的邻接点w)

                    访问w；visited[w]=1；

                    w进栈;

            else

                     x出栈；

 

 

广度优先遍历

 

1.广度优先遍历定义

 

 图的广度优先遍历BFS算法是一个分层搜索的过程，和树的层序遍历算法类同，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。 

2.基本实现思想

 

（1）顶点v入队列。

（2）当队列非空时则继续执行，否则算法结束。

（3）出队列取得队头顶点v；访问顶点v并标记顶点v已被访问。

（4）查找顶点v的第一个邻接顶点col。

（5）若v的邻接顶点col未被访问过的，则col入队列。

（6）继续查找顶点v的另一个新的邻接顶点col，转到步骤（5）。

        直到顶点v的所有未被访问过的邻接点处理完。转到步骤（2）。

广度优先遍历图是以顶点v为起始点，由近至远，依次访问和v有路径相通而且路径长度为1，2，……的顶点。为了使“先被访问顶点的邻接点”先于“后被访问顶点的邻接点”被访问，需设置队列存储访问的顶点。

 

 

3.伪代码

（1）初始化队列Q；visited[n]=0；

（2）访问顶点v；visited[v]=1；顶点v入队列Q；

（3） while（队列Q非空）   

              v=队列Q的对头元素出队；

              w=顶点v的第一个邻接点；

             while（w存在） 

                     如果w未访问，则访问顶点w；

                     visited[w]=1；

                     顶点w入队列Q；

                     w=顶点v的下一个邻接点。