COVID-19:控制疫情 | 唧唧堂论文解析

picture from Internet
专栏介绍
![]()
长按二维码直接进入专栏
本文为唧唧堂《新冠病毒主题论文导读专栏》内一篇论文解析,唧唧堂将在本专栏收录发布所有新冠病毒主题的经济金融社会心理等社科类论文解析导读,同时也或将收录部分医学论文。
本专栏论文收录无截止时限,现已有超100篇NBER工作论文解析中,未来唧唧堂将源源不断把发现的新冠病毒主题论文放入本专栏,期待各位研究人的关注与订阅。点击了解专栏!
唧唧堂现招募更多经济金融研究人加入写作小组,以更快完成本专栏内容的解析产出,解析作者在获得固定稿费同时,还将获得付费阅读收入的部分提成。点击加入写作小组!
本文是针对工作论文《Controlling a Pandemic(控制疫情)》的一篇解析(NBER Working Paper 27046)。该论文作者是Andrew Glover, Jonathan Heathcote, Dirk Krueger, José-Víctor Ríos-Rull。
研究背景与问题
在研究控制疫情的最优政策时,相关文献往往考虑的是均一隔离政策。然而,现实情况中存在着很明显的异质性。比如,老年人患病死亡率比年轻人更高、年轻人隔离的经济成本比老年人更高、经济部门分为可选消费和必需消费等。此外,疫情中人群本身的状态还可以更加细化,比如无症状感染者、轻症和重症之间的区分。另一方面,政府的政策可以更加复杂,比如定向隔离、定向补贴的可能性。[Glover et al., 2020](即本论文)考虑了多种异质化情形组合时的最优政策,构建了一个庞大的模型,考察异质化环境中的最优政策路径。
模型
异质性模拟
这篇论文中所运用的模型仍然是传染病模型和宏观经济模型的组合。不过,此处的传染病模型是在传统的SIR模型上加以细化的“SAFER”模型。SAFER模型将SIR中的I(带有病毒的人)扩充为3个状态——无症状感染者(A,Asymptomatic),轻症患者(F,Flu symptoms),重症患者(Emergency care);而易感者(S, Susceptible)和康复者(R,Recovered)与SIR一致。这一建构方式考虑了染病者I内部的异质化。除此之外,整个人群按照年龄分为年轻人(y,65岁以下,假设占人群的85%)和老年人(o,65岁以上);消费/生产部门按照商品属性分为必需品部门(b,basic)和奢侈品部门(l,luxury)。下文以x上标(年龄/部门/感染状态)代表某一人群的变量,比如x^ybs表示“在必需品部门工作的年轻易感者”的比例,而x^o表示所有老年人的测度(比例)。
重要假设
假设A型人群不知道自己带有病毒;F型患者知道自己带有病毒,因此会停止工作和消费,呆在家中;E型患者需要紧急治疗,因此呆在医院;R型人群对病毒具有永久的免疫力;只有E型患者有死亡的可能,而A型可以转化为F型,F型可以转化为E型,A、F、E三种状态的患者都有直接康复的可能性(变为R)。如果A型患者变为R,她会分不清自己是S、A、R之间的某一状态。
假设μ^b比例的人在必需品部门b工作,1-μ^b比例的人则在奢侈品部门l工作。政府在t时刻的隔离政策m(t)∈[0,1]只对l部门有效,m(t)表示t时刻l部门中受隔离命令而无法工作的工人比例。假设只有年轻人y工作,并且生产函数是关于劳动力测度的线性函数,那么必需品的产值y^b为:
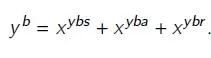
而奢侈品的产值y^l为:

可以看出,模型假设无症状感染者a继续工作,而其余的人都不工作;另外,隔离政策m仅对奢侈品部门有效。为了简化情形,假设奢侈品和必需品为完美替代品,则总产值y为:
假设总产值中有固定部分ηΘ是医疗资源开支,其中Θ是医疗资源的接纳能力(比如床位),η是维护医疗资源的单位成本。
假设疫情的传播有四种途径:工作(w)、消费(c)、亲友(h)和医院(e)。其中,工作和消费这两种途径传播的场所是生产部门和商品部门。现实情况下,必需品和奢侈品都有异质化的细分市场,不同的细分市场中会有不同的社交活动强度。另一方面,病毒会通过工作和消费两种行为进行传播,而某个细分市场的活动强度越大,这个市场中的易感者通过工作或消费而感染病毒的风险也会越高。因此,政府会首先关闭那些活动强度大的奢侈品细分市场(比如KTV、电影院)。为了模拟异质化的细分市场,本文假设工人是均匀分布细分市场i∈[0,1]上。其中,i的值越大表示该市场所需要的社交活动越多(笔者注:参考[Krueger et al., 2020])。假设细分市场i的感染强度系数为(生产端用w做下标,消费端用c做下标)
其中的α是一个表征人与人之间社会活动量的系数。假设政府的隔离政策m只针对奢侈品部门活动强度最大的细分市场(即i∈[1-m, 1]的细分市场),那么剩下细分市场的平均活动量就分别为α_w(1-m)和α_c(1-m)。因此,整个市场生产端的感染强度系数为:
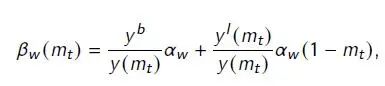
可以看出,β是m的减函数(消费端系数β_c的表达式也类似)。因此,政府的隔离政策通过这个表达式对疫情的动态发展起到抑制作用。令β_h和β_e为常数。
SAFER动态
令总人群的测度为1,则根据年龄-工作部门划分,人群可以分为:
易感者的感染动态由下列迭代方程组给出(将等式两端看作是变量赋值关系)
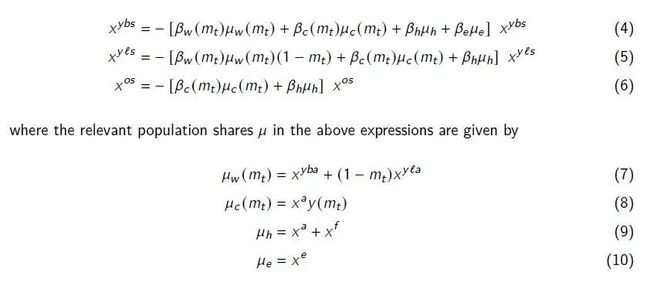
令σ上标(年龄/状态1/状态2)表示某年龄个体从状态1转化为状态2的速率(比如σ^yaf表示“年轻人从无症状a变成轻症f的速率(泊松率)”),再令表征医疗资源饱和程度(e状态人群越多,越大,死亡率越高),则其余人群的动态变化为:
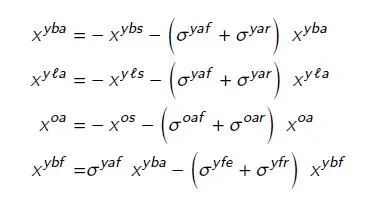
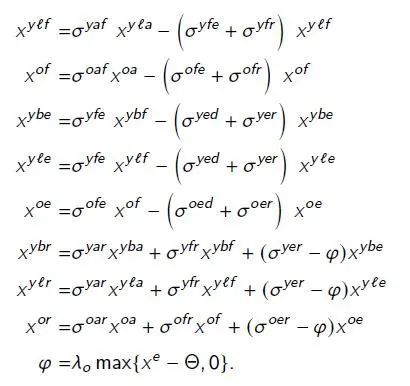
由于本文定义的状态过多,为了形象体现各状态之间的转化,笔者绘制了一张示意图如下:

偏好
人们的偏好由终身效用函数定义。老年人的终身效用函数为:

u_bar表示人活着时享受的效用流(flow utility);u_hat^j表示状态j(j=s, a, f, e, r)时的内含效用(假设s、a、r状态的内含效用都为0,而e、f状态的内含效用小于0,且e小于f);u(c^o)是老年人消费带来的效用;折现率为ρ_o。
类似地,年轻人的效用函数为:
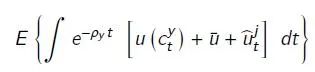
其中ρ_o > ρ_y。由于消费者的预算约束是c_t = n_t,如果政府关掉一些部门,那些部门劳动者的的消费就会受到直接影响。
政府
政府主要有两种政策应对疫情造成的损失——隔离政策和收入再分配。前者的作用已经讨论过了,而后者主要是为了解决隔离政策或染病导致的失业。令所有劳动者的共同消费量为c^w,非劳动者的消费量为c^n,则收入再分配就是要决定每一时刻从劳动者向非劳动者转移多少消费量(因为非劳动者没有收入来源,此处也没有存款,所以转移消费量就是c^n)。假设收入再分配政策是有成本的,成本记为T(cn),其中T()是一个增函数。用μ^n和μ^w分别表示非劳动者和劳动者的测度,即:
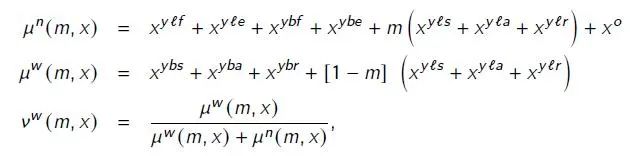
其中v为劳动者占总人数的比例(注意和测度的区别)。那么,总资源约束可以表示如下:

其中y = μ^w。
分析
政府的优化问题是最大化社会福利,其目标函数为: