COVID-19:疫情宏观经济学 | 唧唧堂论文解析

picture from Internet
专栏介绍
![]()
长按二维码直接进入专栏
本文为唧唧堂《新冠病毒主题论文导读专栏》内一篇论文解析,唧唧堂将在本专栏收录发布所有新冠病毒主题的经济金融社会心理等社科类论文解析导读,同时也或将收录部分医学论文。
本专栏论文收录无截止时限,现已有超100篇NBER工作论文解析中,未来唧唧堂将源源不断把发现的新冠病毒主题论文放入本专栏,期待各位研究人的关注与订阅。点击了解专栏!
唧唧堂现招募更多经济金融研究人加入写作小组,以更快完成本专栏内容的解析产出,解析作者在获得固定稿费同时,还将获得付费阅读收入的部分提成。点击加入写作小组!
本文是针对工作论文《The Macroeconomics of Epidemics (疫情宏观经济学)》的一篇解析(NBER Working Paper 26882)。该论文作者是Martin S. Eichenbaum, Sergio Rebelo, 和Mathias Trabandt。
研究背景与问题
疫情席卷全球之际,各国政府和人民都想知道什么才是最优的隔离政策。要解决这个问题,就是要在健康和财富之间做权衡。此论文将传统的传染病模型与宏观经济模型相结合,发现不管是在个体的竞争性均衡还是集体的规划均衡中,要使一个系统中的疫情平息,无论如何都要达到群体免疫(herd immunity)。那么研究疫情宏观经济学的意义就在于找出一条最优化地达到群体免疫的政策路径——既能够降低死亡率和感染率,又能够减小经济损失。这将是一条温和导向群体免疫的路径。除此之外,本文考虑了内生化医疗资源占用、疫苗出现、特效药出现等重要情况,为后续的研究提供了范式。
模型
SIR-Macro模型
1. 疫情前的经济
这部分考虑无疫情情况下的宏观经济模型。经济体中有一个连续统(continuum)的人群,测度为1,并且先验类型(ex ante type)是均一的。每个人都优化如下目标函数:
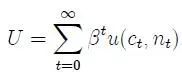
其中,β是折现系数,c和n分别表示消费和工作时间(劳动力供给)。简单起见,假设瞬时效用函数(momentary utility)为如下形式:
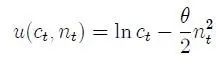
个体代表(representative agent)的约束条件为:
其中,w是真实工资率,μ是消费税率,Γ为趸付的政府转移性支出(government transfer)。本模型以消费税率μ来模拟政府控制疫情的政策,换言之,μ也就是政府制定最优抗疫政策时的控制变量。因此,μ也可以被称作“抑制率”(containment rate)。
个体代表优化问题的一阶条件为:
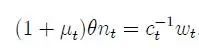
另一方面,完美竞争公司仅用劳动力(工作时间)作为生产要素,生产函数为:
公司选择工作时间以最大化利润:
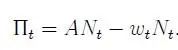
最后,政府的预算约束为:
市场出清条件为 n_t = N_t 与 c_t = C_t。
2. 疫情爆发
疫情期间,人们被分为四种状态:易感(S)、患病(I)、康复(R)和死亡(D)。易感者S被感染有三种途径:一是通过消费行为接触到患病者,直观定义此种途径感染速率为:
π_1 为衡量消费暴露的常数,很明显感染速率与易感者的消费和患病者的消费都正相关;二是通过工作,类似地,感染速率为:
π_2同样为衡量工作暴露的常数;三是通过消费和工作以外的方式与I接触,比如社交等,以π_3作为衡量此种途径的暴露率,感染速率为:
考虑离散时间,则疫情期间某t时刻新增感染量为
进而假设每一时刻患病者I中有π_r部分的人康复,π_d部分的人死亡,则可以写出各种状态人群之间的动态关系:
而总人群Pop(初值为1)的变化:
至此,传染病模型部分已建立完成。下面的部分会将传染病模型和宏观经济模型相整合。
假设疫情开始时有部分的人被感染,即
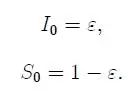
假设所有人都知道上述的模型设定,并且将宏观参数看作是给定的。以上标j来代表j类型人群的状态参数(比如U^r代表康复者R的终身效用,lifetime utility),则类型j个体的预算约束为(对应拉格朗日乘子λ_bt)
其中,c、n是类型j的个体代表可以决定的变量;^j是表征劳动生产率的常数,其中^s = ^r = 1,^i < 1。也就是说,S和R的劳动生产率是一样的,而患病者I较小。这是一个符合现实的假设。
(1) 易感者S
易感者S的终身效用为:
其中,τ表示易感者在t时刻被感染的概率(作为约束,对应拉格朗日乘子λ_τt):
易感者S知道,减少消费或工作都能使她的感染概率降低。S问题的一阶条件为(分别对c、n、τ求导)
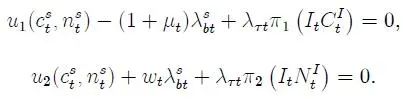
(2) 患病者I
类似地,患病者有终身效用函数如下:
服从前述预算约束。因此,一阶条件为:

(3) 康复者R
R的问题最简单,因为状态不会再变化。其终身效用函数如下:
一阶条件:
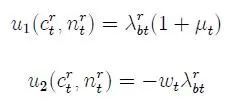
(4) 政府
政府的预算约束:
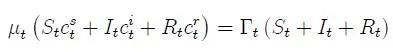
均衡下,市场出清条件为:
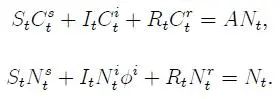
至此,SIR-Macro基线模型及其均衡构建完毕。论文使用数值模拟解出均衡,本解析在后文均衡部分统一展示。
延伸
1. 内生化医疗资源用量