stereo matching的能量函数最小值求解——alpha expansion 和alpha-beta swap算法(图割)
alpha expansion以及alpha-beta swap介绍
- 写在前面的话
- α \alpha α-expansion 和 α − β \alpha-\beta α−βswap的算法流程
- 生成带权图
- α − β \alpha-\beta α−βswap对应的带权图建立
- α − e x p a n s i o n \alpha-expansion α−expansion对应的带权图建立
- 总结
写在前面的话
传统的stereo matching离不开cost computation和cost aggregation两个步骤,在cost aggregation过程中我们习惯在全局能量函数上加入平滑项以达到代价聚合的目的,即
E ( f ) = E d a t a ( f ) + E s m o o t h ( f ) E(f) =E_{data}(f)+E_{smooth}(f) E(f)=Edata(f)+Esmooth(f)
而这个所谓的平滑项 E s m o o t h ( f ) E_{smooth}(f) Esmooth(f)即为计算像素点 p p p处的视差值 f p f_p fp与其邻域内像素点 q q q的视差 f q f_q fq之间的差值(大多数情况下),我们知道对于非边界区域而言,相邻像素点之间的视差必然是连续的,该差值趋近于0,这一特征可用于代价聚合过程,以消除代价计算过程中产生的噪声。但能量函数的最小化问题其实是一个np-hard问题,我们很难在多项式时间内通过暴力求解的手段来获得最优解。故而这里介绍通过 α \alpha α-expansion 和 α − β \alpha-\beta α−βswap算法将最小化求解过程转化为求图的最小割的问题,而图的最小割问题有很多成熟的解法。
α \alpha α-expansion 和 α − β \alpha-\beta α−βswap的算法流程
下图是我们从原作者论文上摘抄下来的算法流程,论文链接
图的上半部分为 α − β \alpha-\beta α−βswap,下半部分为 α \alpha α-expansion算法,现在我们对图中出现的符号作说明(仅针对stereo matching),
f f f为视差图,对于一维图, f f f为一向量,各分量对应各个像素点的视差,对于二维图, f f f为一矩阵,各元素对应图像对应点的视差, f ′ {f}' f′为任意一次 α − β \alpha-\beta α−βswap或 α \alpha α-expansion之后对应的视差图, f ^ \hat{f} f^为对应能量最小化的一次 α − β \alpha-\beta α−βswap或 α \alpha α-expansion之后的视差图。
L \mathcal{L} L为 f f f的各个元素的值分布集合,打个比方 f f f=[1,2,3,3,4,4,6,7],则 L \mathcal{L} L={1,2,3,4,6,7}, α , β \alpha,\beta α,β为 L \mathcal{L} L内的任意两个元素。
故而我们对上述的算法流程进行归纳
(a) α − β \alpha-\beta α−βswap算法流程
1. 开始任意设置视差图 f f f
2. 设置success=0;
3. 对于任意的{ α , β \alpha,\beta α,β} ⊂ L \subset\mathcal{L} ⊂L
3.1 对于 α − β \alpha-\beta α−βswap对应的所有的 f ′ {f}' f′,寻求能量极小值对应的 f ^ \hat{f} f^=argmin E ( f ′ ) E(f') E(f′)
3.2 如果 E ( f ^ ) < E ( f ) E(\hat{f})
4. 如果success=1,返回第二步循环
5. 返回 f f f作为最终结果
(b) α − e x p a n s i o n \alpha-expansion α−expansion算法
1. 开始任意设置视差图 f f f
2. 设置success=0;
3. 对于所有的 α \alpha α ⊂ L \subset\mathcal{L} ⊂L
3.1 对于 α − e x p a n s i o n \alpha-expansion α−expansion对应的所有的 f ′ {f}' f′,寻求能量极小值对应的 f ^ \hat{f} f^=argmin E ( f ′ ) E(f') E(f′)
3.2 如果 E ( f ^ ) < E ( f ) E(\hat{f})
4. 如果success=1,返回第二步循环
5. 返回 f f f作为最终结果
对于以上两个算法,最重要的步骤就是黄色强调部分的寻求能量极小值对应的 f ^ \hat{f} f^,下面我们将主要讲述如何利用图割(graph cut)算法来求解一次 α − β \alpha-\beta α−βswap(或者 α − e x p a n s i o n \alpha-expansion α−expansion)对应的极小值。即如何建立图的源点,汇点,定义各类边的权重,将一次 α − β \alpha-\beta α−βswap(或者 α − e x p a n s i o n \alpha-expansion α−expansion)的极小值求解问题化为求带权图的最小割问题。
生成带权图
本节主要围绕带权图的建立展开,我们知道对于一幅带权图 G = < V , ε > \mathcal{G}=<\mathcal{V,\varepsilon}> G=<V,ε>,它包括一个源点一个汇点,待分类顶点以及连接各顶点与源点和汇点的有权边。为求解一次 α − β \alpha-\beta α−βswap(或者 α − e x p a n s i o n \alpha-expansion α−expansion)对应的极小值,我们应当如何建立相应的带权图,然后利用图割算法求解极小值?
α − β \alpha-\beta α−βswap对应的带权图建立
我们首先讨论 α − β \alpha-\beta α−βswap算法下带权图的建立。首先, α \alpha α和 β \beta β分别为图的源点与汇点,视差图 f f f中视差为 α \alpha α和 β \beta β对应的所有像素点集合为图的顶点集合,连接源点 α \alpha α与顶点的边为 t p α t^\alpha_p tpα,汇点 β \beta β与顶点的边为 t p β t^\beta_p tpβ,统称为 t − l i n k s t-links t−links,连接各相邻顶点的边为 e { p , q } e\{p,q\} e{p,q},称为 n − l i n k s n-links n−links,图的结构如下图所示:
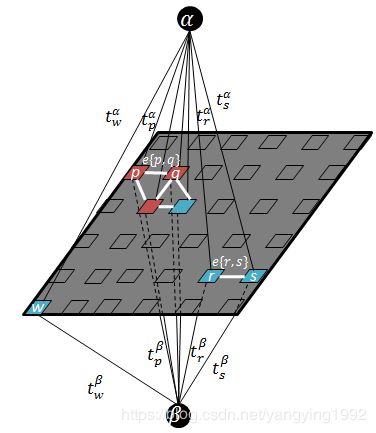
图中红色方块表示视差图 f f f中视差为 α \alpha α的所有像素点集合 P α \mathcal{P_\alpha} Pα,蓝色方块表示视差为 β \beta β的像素点集合 P β \mathcal{P_\beta} Pβ。对于图中各种类型边的权重,我们作如下设置
其中 D p ( α ) D_p(\alpha) Dp(α)表示像素点 p p p的视差值取为 α \alpha α时对应的代价值, D p ( β ) D_p(\beta) Dp(β)表示像素点 p p p的视差值取为 β \beta β时对应的代价值。 V { p , q } ( α , f q ) V_{\{p,q\}}(\alpha,f_q) V{p,q}(α,fq)表示像素点 p p p的视差为 α \alpha α,其相邻像素点 q q q视差为 f q f_q fq时对应的不连续惩罚值。 V { p , q } ( β , f q ) V_{\{p,q\}}(\beta,f_q) V{p,q}(β,fq)表示像素点 p p p的视差为 β \beta β,其相邻像素点 q q q视差为 f q f_q fq时对应的不连续惩罚值。 V { p , q } ( α , β ) V_{\{p,q\}}(\alpha,\beta) V{p,q}(α,β)表示像素点 p p p的视差为 α \alpha α,其相邻像素点 q q q视差为 β \beta β时对应的不连续惩罚值。
到此为止,我们已经由给定的视差图建立了一个包含源点与汇点的连通带权图,那么图的割是什么?顾名思义,割就是将连通图切割为不连通图的边的集合,对于我们建立的带权图,割就是将源点与汇点分开的边集,对于相邻与不相邻像素点,割包含以下6种情况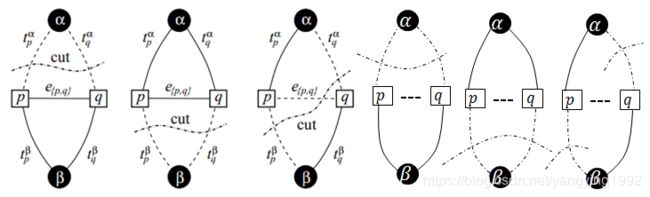
其实归纳起来就是一种情况:源点与汇点之间无连通路径。
对于以上我们建立的连通带权图,存在多个不同的割,能够完成将源点与汇点分开的目标。对于不同的割,我们求解其对应的代价值,即割集内包含的边的权重之和 ∣ C ∣ |\mathcal{C}| ∣C∣。
∣ C ∣ = ∑ p ∈ P α ∪ P β D p ( f p c ) + ∑ p o r q ∈ P α ∪ P β , { p , q } ∈ N V { p , q } ( f p c , f q c ) |\mathcal{C}|=\sum_{p\in\mathcal{P}_{\alpha}\cup \mathcal{P}_{\beta}}D_p(f_p^c)+\sum_{p\ or\ q \in\mathcal{P}_{\alpha}\cup \mathcal{P}_{\beta} ,\{p,q\}\in\mathcal{N}}V_{\{p,q\}}(f_p^c,f_q^c) ∣C∣=p∈Pα∪Pβ∑Dp(fpc)+p or q∈Pα∪Pβ,{p,q}∈N∑V{p,q}(fpc,fqc)
设 K K K为所有本身及其邻域内的点均不在连通图中的顶点对应代价值及不连续惩罚之和,即
K = ∑ p ∉ P α ∪ P β D p ( f p c ) + ∑ p o r q ∉ P α ∪ P β , { p , q } ∈ N V { p , q } ( f p c , f q c ) K=\sum_{p\not\in\mathcal{P}_{\alpha}\cup \mathcal{P}_{\beta}}D_p(f_p^c)+\sum_{p\ or\ q \not\in\mathcal{P}_{\alpha}\cup \mathcal{P}_{\beta} ,\{p,q\}\in\mathcal{N}}V_{\{p,q\}}(f_p^c,f_q^c) K=p∈Pα∪Pβ∑Dp(fpc)+p or q∈Pα∪Pβ,{p,q}∈N∑V{p,q}(fpc,fqc)
对于任意已知的视差图, K K K为一常数,而图像的全局能量函数 E E E为割集代价值和 K K K值之和,即
E = ∣ C ∣ + K E=|\mathcal{C}|+K E=∣C∣+K
对于 α − β \alpha-\beta α−βswap算法来说, K K K为常数,故而,当 ∣ C ∣ |\mathcal{C}| ∣C∣取得极小值时,全局能量函数 E E E也取得极小值。这也说明我们构建的带权连通图的最小割对应了全局能量函数的极小值。很多成熟的算法可以在多项式时间内求解出带权连通图的最小割,这里不再赘述。
本小节的主要目的是讲述如何求解 α − β \alpha-\beta α−βswap算法对应的能量函数极小值,即如何将求极小值问题转化为求解图割算法最小割的问题,包括了连通图的建立,各类边的权重赋值问题。至于对于连通图最小割的求解问题,由于存在很多现有的成熟算法,这里将不再赘述。
α − e x p a n s i o n \alpha-expansion α−expansion对应的带权图建立
我们现在讨论 α − e x p a n s i o n \alpha-expansion α−expansion算法下带权图的建立。首先, α \alpha α和 α ˉ \bar\alpha αˉ分别为图的源点与汇点,视差图 f f f中所有像素点集合为图的顶点集合,连接源点 α \alpha α与顶点的边为 t p α t^\alpha_p tpα,汇点 α ˉ \bar\alpha αˉ与顶点的边为 t p α ˉ t^{\bar\alpha}_p tpαˉ,统称为 t − l i n k s t-links t−links,连接具有相同视差值的各相邻顶点的边为 e { p , q } e\{p,q\} e{p,q},称为 n − l i n k s n-links n−links,在具有不同视差值且相邻的顶点之间插入辅助结点,对于辅助结点,我们只创建三种类型的边 ε { p , q } = { e { p , a } , e { a , q } , t a α ˉ } \varepsilon_{\{p,q\}}=\{e_{\{p,a\}},e_{\{a,q\}},t_a^{\bar\alpha}\} ε{p,q}={e{p,a},e{a,q},taαˉ},图的结构如下图所示(为简便起见,这里只给出了图片为一维图的情况,2维图片的情况读者可参考上面 α − β \alpha-\beta α−βswap算法):
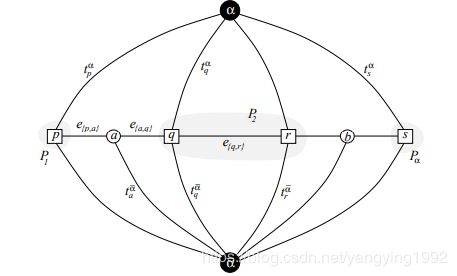
图中包含四个像素点 p , q , r , s p,q,r,s p,q,r,s,隶属三类 P 1 = { p } , P 2 = { q , r } , \mathcal{P}_1=\{p\},\mathcal{P}_2=\{q,r\}, P1={p},P2={q,r},两个插入的辅助结点 a = a { p , q } , b = a { r , s } a=a_{\{p,q\}},b=a_{\{r,s\}} a=a{p,q},b=a{r,s},对于图中各类型的边的权值,我们作如下设置
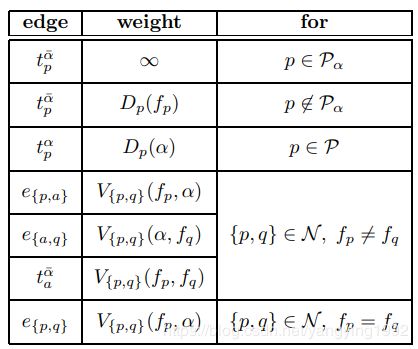
1)当 p p p点的视差为 α \alpha α时,其到汇点 α ˉ \bar\alpha αˉ的边 t p α ˉ t_p^{\bar\alpha} tpαˉ的权重设为 ∞ \infty ∞,这由 α − e x p a n s i o n \alpha-expansion α−expansion名字即可得来,即算法只会让视差值为 α \alpha α的像素数量扩大,其到源点的边 t p α t_p^{\alpha} tpα的权重设为 D p ( α ) D_p(\alpha) Dp(α)为该点视差为 α \alpha α对应的代价值。
2)当 p p p点的视差不为 α \alpha α时,其到汇点 α ˉ \bar\alpha αˉ的边 t p α ˉ t_p^{\bar\alpha} tpαˉ的权重设为 D p ( f p ) D_p(f_p) Dp(fp),为该点视差为 f p f_p fp对应的代价值,其到源点的边 t p α t_p^{\alpha} tpα的权重设为 D p ( α ) D_p(\alpha) Dp(α)为该点视差为 α \alpha α对应的代价值。
3)连接辅助结点 a a a与 p p p点的边 e { p , a } e_{\{p,a\}} e{p,a}的权重设为 V { p , q } ( f p , α ) V_{\{p,q\}}(f_p,\alpha) V{p,q}(fp,α),为该点视差为 f p ≠ α f_p\ne\alpha fp=α时对应的不连续惩罚值。
4)连接辅助结点 a a a与 q q q点的边 e { a , q } e_{\{a,q\}} e{a,q}的权重设为 V { p , q } ( α , f q ) V_{\{p,q\}}(\alpha,f_q ) V{p,q}(α,fq),为该点视差为 f q ≠ α f_q\ne\alpha fq=α时对应的不连续惩罚值。
5)连接辅助结点 a a a与汇点 α ˉ \bar\alpha αˉ的边 t a α ˉ t_a^{\bar\alpha} taαˉ的权重设为 V { p , q } ( f p , f q ) V_{\{p,q\}}(f_p,f_q) V{p,q}(fp,fq),为 p p p点, q q q点的视差分别为 f p f_p fp, f q f_q fq时对应的不连续惩罚值。
6)当 p p p, q q q相邻,且视差 f p = f q f_p=f_q fp=fq相等时,连接 p p p, q q q点的边 e { p , q } e_{\{p,q\}} e{p,q}的权重设为 V { p , q } ( f p , α ) V_{\{p,q\}}(f_p,\alpha) V{p,q}(fp,α),为 p p p或 q q q点视差保持 f p f_p fp不变,剩下另一点的视差变为 α \alpha α时对应的不连续惩罚值。
到此为止,我们已经由给定的视差图及标签 α \alpha α建立了带权连通图。
对于相邻视差不等像素点 p p p, q q q,该带权连通图的最小割 C \mathcal{C} C的割法只有如下图三种情况
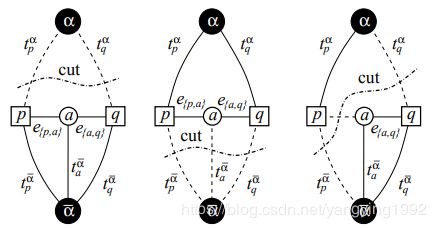
第一种: p p p, q q q均将视差调整为 α \alpha α,此时最小割的代价值仅为 p p p, q q q视差为 α \alpha α时对应的代价值之和
第二种: p p p, q q q视差均不作改变,且都不为 α \alpha α,此时最小割的代价值为, p p p, q q q视差为 f p f_p fp, f q f_q fq时对应的代价值之和 + + + p p p, q q q视差为 f p f_p fp, f q f_q fq时对应的不连续惩罚值
第三种: p p p, q q q视差一个维持不变,一个调整为 α \alpha α,此时最小割的代价值为, p p p, q q q视差为 α \alpha α, f q f_q fq时对应的代价值之和 + + + p p p, q q q视差为 α \alpha α, f q f_q fq时对应的不连续惩罚值。
对于相邻且视差相同点的最小割和上述 α − β \alpha-\beta α−βswap的六种割法相同。
接下来,我们来计算该图的任一割(排除不可能出现最小割的割法)对应的代价值 ∣ C ∣ |\mathcal{C}| ∣C∣
∣ C ∣ = ∑ p ∈ P ∣ C ∩ { t p α , t p α ˉ } ∣ + ∑ f p = f q , { p , q } ∈ N ∣ C ∩ e { p , q } ∣ + ∑ f p ≠ f q , { p , q } ∈ N ∣ C ∩ ε { p , q } ∣ |\mathcal{C}|=\sum_{p\in\mathcal{P}}|\mathcal{C}\cap\{t_p^\alpha,t_p^{\bar\alpha}\}|+\sum_{f_p= f_q ,\{p,q\}\in\mathcal{N}}|\mathcal{C}\cap e_{\{p,q\}}|+\sum_{f_p\ne f_q ,\{p,q\}\in\mathcal{N}}|\mathcal{C}\cap \varepsilon_{\{p,q\}}|\\ ∣C∣=p∈P∑∣C∩{tpα,tpαˉ}∣+fp=fq,{p,q}∈N∑∣C∩e{p,q}∣+fp=fq,{p,q}∈N∑∣C∩ε{p,q}∣
= ∑ p ∈ P D p ( f p c ) + ∑ { p , q } ∈ N V { p , q } ( f p c , f q c ) = E ( f c ) =\sum_{p\in\mathcal{P}}D_p(f_p^c)+\sum_{\{p,q\}\in\mathcal{N}}V_{\{p,q\}}(f_p^c,f_q^c)=E(f^c) =p∈P∑Dp(fpc)+{p,q}∈N∑V{p,q}(fpc,fqc)=E(fc)
(在不可能出现最小割的割法被排除的情况下)该带权连通图的任一割对应的代价值等于全局能量函数的值,故而最小割对应的代价值等于全局能量函数的最小值。此时,我们就完成能一次 α − e x p a n s i o n \alpha-expansion α−expansion情况下能量函数最小值的求解问题,即将能量函数极小值问题转化为求解带权连通图的最小割问题。至于带权连通图最小割问题的求解存在很多成熟的算法,这里不再赘述。
总结
本博文主要讲述了如何将求解能量函数极小值问题转化为求解带权连通图的最小割问题的方法,包括两种建立带权连通图的方法: α − e x p a n s i o n \alpha-expansion α−expansion 和 α − β \alpha-\beta α−βswap算法。讲述了各个顶点赋值以及割边的权重设置,并且证明了对于 α − β \alpha-\beta α−βswap算法最小割的代价值加上一个常数等于全局能量函数的极小值;对于 α − e x p a n s i o n \alpha-expansion α−expansion 算法最小割的代价值等于全局能量函数的极小值。