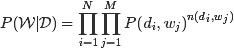通俗理解LDA主题模型
原文链接:
通俗理解LDA主题模型
还是尽量查看原文吧
目录(?)[-]
- 通俗理解LDA主题模型
- 前言
- gamma函数
- 整体把握LDA
- gamma函数
- beta分布
- beta分布
- Beta-Binomial 共轭
- 共轭先验分布
- 从beta分布推广到Dirichlet 分布
- Dirichlet 分布
- Dirichlet 分布
- Dirichlet-Multinomial 共轭
- 主题模型LDA
- 各个基础模型
- Unigram model
- Mixture of unigrams model
- PLSA模型
- 什么是pLSA模型
- EM算法的简单介绍
- EM算法估计pLSA的两未知参数
- LDA模型
- pLSA跟LDA的对比生成文档与参数估计
- LDA生成文档过程的进一步理解
- pLSA跟LDA的概率图对比
- pLSA跟LDA参数估计方法的对比
- LDA参数估计Gibbs采样
- 读者微评
- 参考文献与推荐阅读
- 后记
- 各个基础模型
通俗理解LDA主题模型
0 前言
印象中,最开始听说“LDA”这个名词,是缘于rickjin在2013年3月写的一个LDA科普系列,叫LDA数学八卦,我当时一直想看来着,记得还打印过一次,但不知是因为这篇文档的前序铺垫太长(现在才意识到这些“铺垫”都是深刻理解LDA 的基础,但如果没有人帮助初学者提纲挈领、把握主次、理清思路,则很容易陷入LDA的细枝末节之中),还是因为其中的数学推导细节太多,导致一直没有完整看完过。
2013年12月,在我组织的Machine Learning读书会第8期上,@夏粉_百度 讲机器学习中排序学习的理论和算法研究,@沈醉2011 则讲主题模型的理解,又一次碰到了主题模型,当时貌似只记得沈博讲了一个汪峰写歌词的例子,依然没有理解LDA到底是怎样一个东西(但理解了LDA之后,再看沈博主题模型的PPT会很赞)。
直到昨日下午,机器学习班第12次课上,邹博讲完LDA之后,才真正明白LDA原来是那么一个东东!上完课后,趁热打铁,再次看LDA数学八卦,发现以前看不下去的文档再看时竟然一路都比较顺畅,一口气看完大部。看完大部后,思路清晰了,知道理解LDA,可以分为下述5个步骤:
- 一个函数:gamma函数
- 四个分布:二项分布、多项分布、beta分布、Dirichlet分布
- 一个概念和一个理念:共轭先验和贝叶斯框架
- 两个模型:pLSA、LDA(在本文第4 部分阐述)
- 一个采样:Gibbs采样
而我向来不满足于一个东西只是自己理解,如果自己理解了,我想把这个东西写成博客或开班,以让更多的人理解,从而共同欣赏其中的美妙。无论是写面试题解,还是写算法,或者这个机器学习系列,好东西就该大家一起分享,故本文诞生了。
本文按照上述5个步骤来阐述,希望读者看完本文后,能对LDA有个尽量清晰完整的了解。并且,本文基于邹博讲LDA的PPT、rickjin的LDA数学八卦及其它参考资料写就,可以定义为一篇学习笔记或课程笔记,当然,后续不断加入了很多自己的理解。若有任何问题,欢迎随时于本文评论下指出,thanks。
1 gamma函数
1.0 整体把握LDA
开篇之前,得先说下关于LDA,其实有两种含义,一种是线性判别分析(Linear Discriminant Analysis),一种是概率主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),本文讲后者(前者会在后面的博客中阐述)。
开篇之始,我也还是要简单说下LDA的整体思想,不然我怕你看了半天,铺了太长的前奏,却依然因没见到LDA的影子而显得“心浮气躁”,导致不想再继续看下去。所以,先给你吃一颗定心丸,明白整体框架后,咱们再一步步抽丝剥茧,展开来论述。
按照wiki上的介绍,LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,是一种主题模型,它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。此外,一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
LDA的这三位作者在原始论文中给了一个简单的例子。比如假设事先给定了这几个主题:Arts、Budgets、Children、Education,然后通过学习的方式,获取每个主题Topic对应的词语。如下图所示:
然后以一定的概率选取上述某个主题,再以一定的概率选取那个主题下的某个单词,不断的重复这两步,最终生成如下图所示的一篇文章(其中不同颜色的词语分别对应上图中不同主题下的词):

而当我们看到一篇文章后,往往喜欢推测这篇文章是如何生成的,我们可能会认为某个作者先确定这篇文章的几个主题,然后围绕这几个主题遣词造句,表达成文。LDA就是要干这事:根据给定的一篇文档,推测其主题分布。
- 从狄利克雷分布
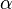 中取样生成文档 i 的主题分布
中取样生成文档 i 的主题分布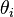
- 从主题的多项式分布
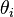 中取样生成文档i第 j 个词的主题
中取样生成文档i第 j 个词的主题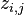
- 从狄利克雷分布
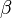 中取样生成主题
中取样生成主题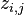 对应的词语分布
对应的词语分布
- 从词语的多项式分布
 中采样最终生成词语
中采样最终生成词语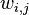
其中,类似Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布。
此外,LDA的图模型结构如下图所示(类似贝叶斯网络结构):
恩,不错,短短6句话整体概括了整个LDA的主体思想!但也是上面短短6句话,却接连不断或重复出现了二项分布、多项式分布、beta分布、狄利克雷分布(Dirichlet分布)、共轭先验概率分布、取样,那么请问,这些都是啥呢?
这里先简单解释下二项分布、多项分布、beta分布、Dirichlet 分布这4个分布。
- 二项分布(Binomial distribution)。
- 多项分布,是二项分布扩展到多维的情况。
- Beta分布,二项分布的共轭先验分布。
,

。
- Dirichlet分布,是beta分布在高维度上的推广。
OK,接下来,咱们就按照本文开头所说的思路:“一个函数:gamma函数,四个分布:二项分布、多项分布、beta分布、Dirichlet分布,外加一个概念和一个理念:共轭先验和贝叶斯框架,两个模型:pLSA、LDA(文档-主题,主题-词语),一个采样:Gibbs采样”一步步详细阐述,争取给读者一个尽量清晰完整的LDA。
(当然,如果你不想深究背后的细节原理,只想整体把握LDA的主体思想,可直接跳到本文第4 部分,看完第4部分后,若还是想深究背后的细节原理,可再回到此处开始看)
1.1 gamma函数
咱们先来考虑一个问题(此问题1包括下文的问题2-问题4皆取材自LDA数学八卦):
- 问题1 随机变量
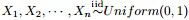
- 把这n 个随机变量排序后得到顺序统计量
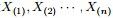
- 然后请问
 的分布是什么。
的分布是什么。
为解决这个问题,可以尝试计算![]() 落在区间[x,x+Δx]的概率。即求下述式子的值:
落在区间[x,x+Δx]的概率。即求下述式子的值:
首先,把 [0,1] 区间分成三段 [0,x),[x,x+Δx],(x+Δx,1],然后考虑下简单的情形:即假设n 个数中只有1个落在了区间 [x,x+Δx]内,由于这个区间内的数X(k)是第k大的,所以[0,x)中应该有 k−1 个数,(x+Δx,1] 这个区间中应该有n−k 个数。如下图所示:
至此,本节开头提出的问题得到解决。然仔细观察![]() 的概率密度函数,发现式子的最终结果有阶乘,联想到阶乘在实数上的推广
的概率密度函数,发现式子的最终结果有阶乘,联想到阶乘在实数上的推广![]() 函数:
函数:
两者结合是否会产生奇妙的效果呢?考虑到![]() 具有如下性质:
具有如下性质:
故将代入到
![]() 的概率密度函数
的概率密度函数![]() 中,可得:
中,可得:
然后取![]() = k,
= k,![]() = n−k+1,转换
= n−k+1,转换![]() 得到:
得到:
如果熟悉beta分布的朋友,可能会惊呼:竟然推出了beta分布!
2 beta分布
2.1 beta分布
 的beta分布通常写作:
的beta分布通常写作:
2.2 Beta-Binomial 共轭
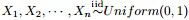 ,对应的顺序统计量是
,对应的顺序统计量是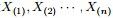 ,需要猜测
,需要猜测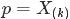 ;
;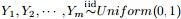 ,
,  中有
中有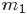 个比p小,
个比p小,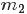 个比
个比 大;
大;- 那么,请问
 的分布是什么。
的分布是什么。
- 为了猜测
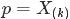 ,在获得一定的观测数据前,我们对
,在获得一定的观测数据前,我们对 的认知是:
的认知是: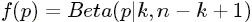 ,此称为
,此称为 的先验分布;
的先验分布; - 然后为了获得这个结果“
 中有
中有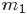 个比p小,
个比p小,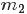 个比
个比 大”,针对
大”,针对 是做了
是做了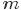 次贝努利实验,所以
次贝努利实验,所以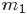 服从二项分布
服从二项分布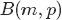 ;
; - 在给定了来自数据提供的
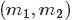 的知识后,
的知识后, 的后验分布变为
的后验分布变为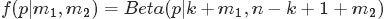 。
。
- 先验分布
 + 样本信息
+ 样本信息
 后验分布
后验分布
针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial共轭。换言之,Beta分布是二项式分布的共轭先验概率分布。
二项分布和Beta分布是共轭分布意味着,如果我们为二项分布的参数p选取的先验分布是Beta分布,那么以p为参数的二项分布用贝叶斯估计得到的后验分布仍然服从Beta分布。
2.3 共轭先验分布
- 可否根据新观测数据X,更新参数θ?
- 根据新观测数据可以在多大程度上改变参数θ,即
- 当重新估计θ的时候,给出新参数值θ的新概率分布,即P(θ|x)。
所以,如果我们选取P(x|θ)的共轭先验作为P(θ)的分布,那么P(x|θ)乘以P(θ),然后归一化的结果P(θ|x)跟和P(θ)的形式一样。换句话说,先验分布是P(θ),后验分布是P(θ|x), 先验分布跟后验分布同属于一个分布族,故称该分布族是θ的共轭先验分布(族)。
2.4 从beta分布推广到Dirichlet 分布
从而求得
最后的这个结果意味着对于Beta 分布的随机变量,其均值(期望)可以用![]() 来估计。此外,狄利克雷Dirichlet 分布也有类似的结论,即如果
来估计。此外,狄利克雷Dirichlet 分布也有类似的结论,即如果![]() ,同样可以证明有下述结论成立:
,同样可以证明有下述结论成立:
那什么是Dirichlet 分布呢?简单的理解Dirichlet 分布就是一组连续多变量概率分布,是多变量普遍化的beta分布。为了纪念德国数学家约翰·彼得·古斯塔夫·勒热纳·狄利克雷(Peter Gustav Lejeune Dirichlet)而命名。狄利克雷分布常作为贝叶斯统计的先验概率。
3 Dirichlet 分布
3.1 Dirichlet 分布
根据wikipedia上的介绍,维度K ≥ 2(x1,x2…xK-1维,共K个)的狄利克雷分布在参数α1, ..., αK > 0上、基于欧几里得空间RK-1里的勒贝格测度有个概率密度函数,定义为:
其中,![]() 相当于是多项beta函数
相当于是多项beta函数
且![]()
此外,x1+x2+…+xK-1+xK=1,x1,x2…xK-1>0,且在(K-1)维的单纯形上,其他区域的概率密度为0。
当然,也可以如下定义Dirichlet 分布
其中的![]() 称为Dirichlet 分布的归一化系数:
称为Dirichlet 分布的归一化系数:
3.2 Dirichlet-Multinomial 共轭
下面,在2.2节问题2的基础上继续深入,引出问题3。
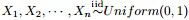 ,
,- 排序后对应的顺序统计量
 ,
, - 问
 的联合分布是什么?
的联合分布是什么?
从而有:
继而得到于是我们得到![]() 的联合分布为:
的联合分布为:
观察上述式子的最终结果,可以看出上面这个分布其实就是3维形式的 Dirichlet 分布
令![]() ,于是分布密度可以写为
,于是分布密度可以写为
这个就是一般形式的3维 Dirichlet 分布,即便![]() 延拓到非负实数集合,以上概率分布也是良定义的。
延拓到非负实数集合,以上概率分布也是良定义的。
将Dirichlet分布的概率密度函数取对数,绘制对称Dirichlet分布的图像如下图所示(截取自wikipedia上):
上图中,取K=3,也就是有两个独立参数x1,x2,分别对应图中的两个坐标轴,第三个参数始终满足x3=1-x1-x2且α1=α2=α3=α,图中反映的是参数α从α=(0.3, 0.3, 0.3)变化到(2.0, 2.0, 2.0)时的概率对数值的变化情况。
为了论证Dirichlet分布是多项式分布的共轭先验概率分布,下面咱们继续在上述问题3的基础上再进一步,提出问题4。
- 问题4
 ,排序后对应的顺序统计量
,排序后对应的顺序统计量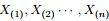
- 令
 ,
,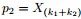 ,
,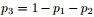 (此处的p3非变量,只是为了表达方便),现在要猜测
(此处的p3非变量,只是为了表达方便),现在要猜测 ;
; 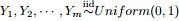 ,Yi中落到
,Yi中落到 ,
,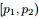 ,
,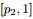 三个区间的个数分别为 m1,m2,m3,m=m1+m2+m3;
三个区间的个数分别为 m1,m2,m3,m=m1+m2+m3;- 问后验分布
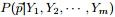 的分布是什么。
的分布是什么。
为了方便讨论,记![]() ,及
,及![]() ,根据已知条件“
,根据已知条件“![]() ,Yi中落到
,Yi中落到![]() ,
,![]() ,
,![]() 三个区间的个数分别为 m1,m2”,可得
三个区间的个数分别为 m1,m2”,可得![]() 、
、![]() 分别是这m+n个数中第
分别是这m+n个数中第![]() 大、第
大、第![]() 大的数。于是,后验分布
大的数。于是,后验分布![]() 应该为
应该为![]() ,即一般化的形式表示为:
,即一般化的形式表示为:![]() 。
。
同样的,按照贝叶斯推理的逻辑,可将上述过程整理如下:
- 我们要猜测参数
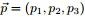 ,其先验分布为
,其先验分布为 ;
; - 数据Yi落到三个区间
 ,
,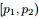 ,
,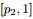 的个数分别为
的个数分别为 ,所以
,所以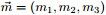 服从多项分布
服从多项分布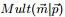
- 在给定了来自数据提供的知识
 后,
后,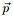 的后验分布变为
的后验分布变为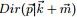
上述贝叶斯分析过程的直观表述为:
令![]() ,可把
,可把![]() 从整数集合延拓到实数集合,从而得到更一般的表达式如下:
从整数集合延拓到实数集合,从而得到更一般的表达式如下:
4 主题模型LDA
在开始下面的旅程之前,先来总结下我们目前所得到的最主要的几个收获:
- 通过上文的第2.2节,我们知道beta分布是二项式分布的共轭先验概率分布:
- “对于非负实数
 和
和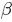 ,我们有如下关系
,我们有如下关系
- “对于非负实数
其中
对应的是二项分布
的计数。针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial 共轭。”
- 通过上文的3.2节,我们知道狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布:
- “ 把
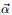 从整数集合延拓到实数集合,从而得到更一般的表达式如下:
从整数集合延拓到实数集合,从而得到更一般的表达式如下:
- “ 把
针对于这种观测到的数据符合多项分布,参数的先验分布和后验分布都是Dirichlet 分布的情况,就是 Dirichlet-Multinomial 共轭。 ”
-
以及贝叶斯派思考问题的固定模式:
- 先验分布
 + 样本信息
+ 样本信息
 后验分布
后验分布
上述思考模式意味着,新观察到的样本信息将修正人们以前对事物的认知。换言之,在得到新的样本信息之前,人们对 的认知是先验分布
的认知是先验分布
 ,在得到新的样本信息
,在得到新的样本信息
 后,人们对
后,人们对
 的认知为
的认知为
 。
。
- 先验分布
- 顺便提下频率派与贝叶斯派各自不同的思考方式:
- 频率派把需要推断的参数θ看做是固定的未知常数,即概率
 虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布;
虽然是未知的,但最起码是确定的一个值,同时,样本X 是随机的,所以频率派重点研究样本空间,大部分的概率计算都是针对样本X 的分布; - 而贝叶斯派的观点则截然相反,他们认为待估计的参数
 是随机变量,服从一定的分布,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数
是随机变量,服从一定的分布,而样本X 是固定的,由于样本是固定的,所以他们重点研究的是参数 的分布。
的分布。
- 频率派把需要推断的参数θ看做是固定的未知常数,即概率
OK,在杀到终极boss——LDA模型之前,再循序渐进理解基础模型:Unigram model、mixture of unigrams model,以及跟LDA最为接近的pLSA模型。
为了方便描述,首先定义一些变量:
 表示词,
表示词,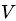 表示所有单词的个数(固定值)
表示所有单词的个数(固定值)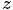 表示主题,
表示主题,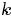 是主题的个数(预先给定,固定值)
是主题的个数(预先给定,固定值)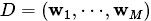 表示语料库,其中的
表示语料库,其中的 是语料库中的文档数(固定值)
是语料库中的文档数(固定值)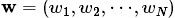 表示文档,其中的
表示文档,其中的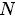 表示一个文档中的词数(随机变量)
表示一个文档中的词数(随机变量)
4.1 各个基础模型
4.1.1 Unigram model
对于文档![]() ,用
,用![]() 表示词
表示词![]() 的先验概率,生成文档
的先验概率,生成文档![]() 的概率为:
的概率为:
其图模型为(图中被涂色的w表示可观测变量,N表示一篇文档中总共N个单词,M表示M篇文档):
或为:
unigram model假设文本中的词服从Multinomial分布,而我们已经知道Multinomial分布的先验分布为Dirichlet分布。
上图中的![]() 表示在文本中观察到的第n个词,n∈[1,N]表示该文本中一共有N个单词。加上方框表示重复,即一共有N个这样的随机变量
表示在文本中观察到的第n个词,n∈[1,N]表示该文本中一共有N个单词。加上方框表示重复,即一共有N个这样的随机变量![]() 。其中,p和α是隐含未知变量:
。其中,p和α是隐含未知变量:
- p是词服从的Multinomial分布的参数
- α是Dirichlet分布(即Multinomial分布的先验分布)的参数。
一般α由经验事先给定,p由观察到的文本中出现的词学习得到,表示文本中出现每个词的概率。
4.1.2 Mixture of unigrams model
4.2 PLSA模型
4.2.1 什么是pLSA模型
- 1. 假设你每写一篇文档会制作一颗K面的“文档-主题”骰子(扔此骰子能得到K个主题中的任意一个),和K个V面的“主题-词项” 骰子(每个骰子对应一个主题,K个骰子对应之前的K个主题,且骰子的每一面对应要选择的词项,V个面对应着V个可选的词)。
- 比如可令K=3,即制作1个含有3个主题的“文档-主题”骰子,这3个主题可以是:教育、经济、交通。然后令V = 3,制作3个有着3面的“主题-词项”骰子,其中,教育主题骰子的3个面上的词可以是:大学、老师、课程,经济主题骰子的3个面上的词可以是:市场、企业、金融,交通主题骰子的3个面上的词可以是:高铁、汽车、飞机。
- 2. 每写一个词,先扔该“文档-主题”骰子选择主题,得到主题的结果后,使用和主题结果对应的那颗“主题-词项”骰子,扔该骰子选择要写的词。
- 先扔“文档-主题”的骰子,假设(以一定的概率)得到的主题是教育,所以下一步便是扔教育主题筛子,(以一定的概率)得到教育主题筛子对应的某个词:大学。
- 3. 最后,你不停的重复扔“文档-主题”骰子和”主题-词项“骰子,直到完成某一篇文档,重复这方法M次,则写完M篇文档。
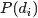 表示海量文档中某篇文档被选中的概率。
表示海量文档中某篇文档被选中的概率。
 表示词
表示词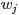 在给定文档
在给定文档 中出现的概率。
中出现的概率。
- 怎么计算得到呢?针对海量文档,对所有文档进行分词后,得到一个词汇列表,这样每篇文档就是一个词语的集合。对于每个词语,用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率
 。
。
- 怎么计算得到呢?针对海量文档,对所有文档进行分词后,得到一个词汇列表,这样每篇文档就是一个词语的集合。对于每个词语,用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率
- 各个主题z在文档d中出现的概率分布称之为主题分布,
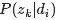 表示具体某个主题
表示具体某个主题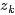 在给定文档
在给定文档 下出现的概率。
下出现的概率。 - 各个词语w在主题z下出现的概率分布称之为词语分布,
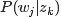 表示具体某个词
表示具体某个词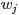 在给定主题
在给定主题 下出现的概率。
下出现的概率。
- 与主题关系越密切的词,其条件概率
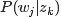 越大。
越大。
- 与主题关系越密切的词,其条件概率
- 按照概率
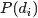 选择一篇文档
选择一篇文档
- 选定文档
 后,从主题分布中按照概率
后,从主题分布中按照概率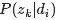 选择一个隐含的主题类别
选择一个隐含的主题类别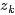
- 选定
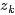 后,从词分布中按照概率
后,从词分布中按照概率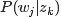 选择一个词
选择一个词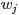
由于![]() 可事先计算求出,而
可事先计算求出,而![]() 和
和![]() 未知,所以
未知,所以![]() 就是我们要估计的参数(值),通俗点说,就是要最大化这个θ。
就是我们要估计的参数(值),通俗点说,就是要最大化这个θ。
用什么方法进行估计呢,常用的参数估计方法有极大似然估计MLE、最大后验证估计MAP、贝叶斯估计等等。因为该待估计的参数中含有隐变量z,所以我们可以考虑EM算法。
4.2.2 EM算法的简单介绍
EM算法,全称为Expectation-maximization algorithm,为期望最大算法,其基本思想是:首先随机选取一个值去初始化待估计的值![]() ,然后不断迭代寻找更优的
,然后不断迭代寻找更优的![]() 使得其似然函数likelihood
使得其似然函数likelihood ![]() 比原来的
比原来的![]() 要大。换言之,假定现在得到了
要大。换言之,假定现在得到了![]() ,想求
,想求![]() ,使得
,使得
EM的关键便是要找到![]() 的一个下界
的一个下界![]() (注:
(注:![]() ,其中,X表示已经观察到的随机变量),然后不断最大化这个下界,通过不断求解下界
,其中,X表示已经观察到的随机变量),然后不断最大化这个下界,通过不断求解下界![]() 的极大化,从而逼近要求解的似然函数
的极大化,从而逼近要求解的似然函数![]() 。
。
所以EM算法的一般步骤为:
- 1. 随机选取或者根据先验知识初始化
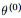 ;
; - 2. 不断迭代下述两步
- ①给出当前的参数估计
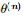 ,计算似然函数
,计算似然函数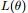 的下界
的下界
- ②重新估计参数θ,即求
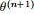 ,使得
,使得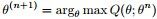
- ①给出当前的参数估计
- 3. 上述第二步后,如果
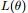 收敛(即
收敛(即 收敛)则退出算法,否则继续回到第二步。
收敛)则退出算法,否则继续回到第二步。
上述过程好比在二维平面上,有两条不相交的曲线,一条曲线在上(简称上曲线),一条曲线在下(简称下曲线),下曲线为上曲线的下界。现在对上曲线未知,只已知下曲线,为了求解上曲线的最高点,我们试着不断增大下曲线,使得下曲线不断逼近上曲线,下曲线在某一个点达到局部最大值并与上曲线在这点的值相等,记录下这个值,然后继续增大下曲线,寻找下曲线上与上曲线上相等的值,迭代到![]() 收敛(即
收敛(即![]() 收敛)停止,从而利用当前下曲线上的局部最大值当作上曲线的全局最大值(换言之,EM算法不保证一定能找到全局最优值)。如下图所示:
收敛)停止,从而利用当前下曲线上的局部最大值当作上曲线的全局最大值(换言之,EM算法不保证一定能找到全局最优值)。如下图所示:
以下是详细介绍。
假定有训练集![]() ,包含m个独立样本,希望从中找到该组数据的模型p(x,z)的参数。
,包含m个独立样本,希望从中找到该组数据的模型p(x,z)的参数。
然后通过极大似然估计建立目标函数--对数似然函数:
这里,z是隐随机变量,直接找到参数的估计是很困难的。我们的策略是建立![]() 的下界,并且求该下界的最大值;重复这个过程,直到收敛到局部最大值。
的下界,并且求该下界的最大值;重复这个过程,直到收敛到局部最大值。
令Qi是z的某一个分布,Qi≥0,且结合Jensen不等式,有:
为了寻找尽量紧的下界,我们可以让使上述等号成立,而若要让等号成立的条件则是:
换言之,有以下式子成立:![]() ,且由于有:
,且由于有:![]()
所以可得:
最终得到EM算法的整体框架如下:
OK,EM算法还会在本博客后面的博文中具体阐述。接下来,回到pLSA参数的估计问题上。
4.2.3 EM算法估计pLSA的两未知参数
首先尝试从矩阵的角度来描述待估计的两个未知变量![]() 和
和![]() 。
。
- 假定用
 表示词表
表示词表 在主题
在主题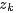 上的一个多项分布,则
上的一个多项分布,则 可以表示成一个向量,每个元素
可以表示成一个向量,每个元素 表示词项
表示词项 出现在主题
出现在主题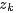 中的概率,即
中的概率,即
- 用
 表示所有主题
表示所有主题 在文档
在文档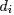 上的一个多项分布,则
上的一个多项分布,则 可以表示成一个向量,每个元素
可以表示成一个向量,每个元素 表示主题
表示主题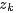 出现在文档
出现在文档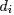 中的概率,即
中的概率,即
这样,巧妙的把![]() 和
和![]() 转换成了两个矩阵。换言之,最终我们要求解的参数是这两个矩阵:
转换成了两个矩阵。换言之,最终我们要求解的参数是这两个矩阵:
由于词和词之间是互相独立的,于是可以得到整篇文档的词的分布;
并且文档和文档也是互相独立的,于是我们可以得到整个样本的词的分布:
其中,![]() 表示词项
表示词项![]() 在文档
在文档![]() 中的词频,
中的词频,![]() 表示文档di中词的总数,显然有
表示文档di中词的总数,显然有![]() 。
。
于是,可以很容易写出样本分布的对数似然函数:
我们需要最大化对数似然函数来求解参数,对于这种含有隐变量的最大似然估计,下面轮到EM方法上场。
E-step:假定参数已知,计算此时隐变量的后验概率。
利用贝叶斯法则,可以得到:
M-step:带入隐变量的后验概率,最大化样本分布的对数似然函数,求解相应的参数。
观察上面的对数似然函数![]() ,由于
,由于![]() 也就是文档长度可以单独从样本计算,可以去掉不影响最大化似然函数;此外,根据E-step的计算结果,把
也就是文档长度可以单独从样本计算,可以去掉不影响最大化似然函数;此外,根据E-step的计算结果,把 ![]() 代入
代入![]() ,于是我们最大化下面这个函数即可:
,于是我们最大化下面这个函数即可:
这是一个多元函数求极值问题,并且已知有如下约束条件:
一般处理这种带有约束条件的极值问题,我们常用的方法是拉格朗日乘数法,引入拉格朗日乘子把约束条件和多元函数结合在一起,转化为无条件极值问题。这里我们引入两个乘子![]() 和
和![]() ,可以写出拉格朗日函数,如下:
,可以写出拉格朗日函数,如下:
需要求解![]() 和
和![]() ,分别求偏导,取0,可以得到如下两个等式:
,分别求偏导,取0,可以得到如下两个等式:
消去拉格朗日乘子,最终可估计出参数:
综上,在pLSA中:
- 由于
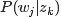 和
和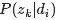 未知,所以我们用EM算法去估计
未知,所以我们用EM算法去估计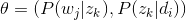 这个参数的值。
这个参数的值。 - 而后,用
 表示词项
表示词项 出现在主题
出现在主题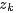 中的概率,即
中的概率,即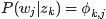 ,用
,用 表示主题
表示主题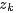 出现在文档
出现在文档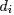 中的概率,即
中的概率,即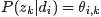 ,从而把
,从而把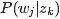 转换成了“主题-词项”矩阵Φ(主题生成词),把
转换成了“主题-词项”矩阵Φ(主题生成词),把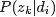 转换成了“文档-主题”矩阵Θ(文档生成主题)。
转换成了“文档-主题”矩阵Θ(文档生成主题)。 - 最终求解出
 、
、 。
。
4.3 LDA模型
事实上,理解了pLSA模型,也就差不多快理解了LDA模型,因为LDA就是在pLSA的基础上加层贝叶斯框架,即LDA就是pLSA的贝叶斯版本(正因为LDA被贝叶斯化了,所以才需要考虑历史先验知识,才加的两个先验参数)。
4.3.1 pLSA跟LDA的对比:生成文档与参数估计
回顾下pLSA模型的整个过程:
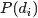 表示海量文档中某篇文档被选中的概率。
表示海量文档中某篇文档被选中的概率。- 各个主题z在文档d中出现的概率分布称之为主题分布,
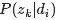 表示具体某个主题
表示具体某个主题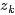 在给定文档
在给定文档 下出现的概率。
下出现的概率。 - 各个词语w在主题z下出现的概率分布称之为词语分布,
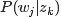 表示具体某个词
表示具体某个词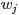 在给定主题
在给定主题 下出现的概率。
下出现的概率。
- 与主题关系越密切的词,其条件概率
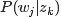 越大。
越大。
- 与主题关系越密切的词,其条件概率
- 按照概率
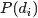 选择一篇文档
选择一篇文档
- 选定文档
 后,确定文章的主题分布
后,确定文章的主题分布 - 从主题分布中按照概率
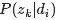 选择一个隐含的主题类别
选择一个隐含的主题类别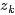
- 选定
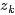 后,确定主题下的词分布
后,确定主题下的词分布 - 从词分布中按照概率
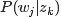 选择一个词
选择一个词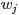 ”
”
下面,咱们对比下本文开头所述的LDA模型中一篇文档生成的方式是怎样的:
- 按照先验概率
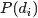 选择一篇文档
选择一篇文档
- 从狄利克雷分布(即Dirichlet分布)
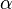 中取样生成文档
中取样生成文档  的主题分布
的主题分布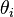 ,换言之,主题分布
,换言之,主题分布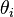 由超参数为
由超参数为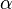 的Dirichlet分布生成
的Dirichlet分布生成 - 从主题的多项式分布
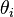 中取样生成文档
中取样生成文档 第 j 个词的主题
第 j 个词的主题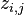
- 从狄利克雷分布(即Dirichlet分布)
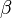 中取样生成主题
中取样生成主题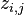 对应的词语分布
对应的词语分布 ,换言之,词语分布
,换言之,词语分布 由参数为
由参数为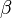 的Dirichlet分布生成
的Dirichlet分布生成 - 从词语的多项式分布
 中采样最终生成词语
中采样最终生成词语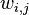 ”
”
- pLSA中,主题分布和词分布确定后,以一定的概率(
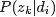 、
、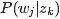 )分别选取具体的主题和词项,生成好文档。而后根据生成好的文档反推其主题分布、词分布时,最终用EM算法(极大似然估计思想)求解出了两个未知但固定的参数的值:
)分别选取具体的主题和词项,生成好文档。而后根据生成好的文档反推其主题分布、词分布时,最终用EM算法(极大似然估计思想)求解出了两个未知但固定的参数的值: (由
(由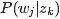 转换而来)和
转换而来)和 (由
(由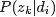 转换而来)。
转换而来)。
- 文档d产生主题z的概率,主题z产生单词w的概率都是两个固定的值。
- 举个文档d产生主题z的例子。给定一篇文档d,主题分布是一定的,比如{ P(zi|d), i = 1,2,3 }可能就是{0.4,0.5,0.1},表示z1、z2、z3,这3个主题被文档d选中的概率都是个固定的值:P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1,如下图所示(图截取自沈博PPT上):
- 文档d产生主题z的概率,主题z产生单词w的概率都是两个固定的值。
- 但在贝叶斯框架下的LDA中,我们不再认为主题分布(各个主题在文档中出现的概率分布)和词分布(各个词语在某个主题下出现的概率分布)是唯一确定的(而是随机变量),而是有很多种可能。但一篇文档总得对应一个主题分布和一个词分布吧,怎么办呢?LDA为它们弄了两个Dirichlet先验参数,这个Dirichlet先验为某篇文档随机抽取出某个主题分布和词分布。
- 文档d产生主题z(准确的说,其实是Dirichlet先验为文档d生成主题分布Θ,然后根据主题分布Θ产生主题z)的概率,主题z产生单词w的概率都不再是某两个确定的值,而是随机变量。
- 还是举文档d具体产生主题z的例子。给定一篇文档d,现在有多个主题z1、z2、z3,它们的主题分布{ P(zi|d), i = 1,2,3 }可能是{0.4,0.5,0.1},也可能是{0.2,0.2,0.6},即这些主题被d选中的概率都不再认为是确定的值,可能是P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1,也有可能是P(z1|d) = 0.2、P(z2|d) = 0.2、P(z3|d) = 0.6等等(相信你看到了,同是主题z2,但前后被产生的概率先是0.5后是0.2,即主题z2被产生的概率大小是不确定的),而主题分布到底是哪个取值集合我们不确定(为什么?这就是贝叶斯派的核心思想,把未知参数当作是随机变量,不再认为是某一个确定的值),但其先验分布是dirichlet 分布,所以可以从无穷多个主题分布中按照dirichlet 先验随机抽取出某个主题分布出来。如下图所示(图截取自沈博PPT上):
- 文档d产生主题z(准确的说,其实是Dirichlet先验为文档d生成主题分布Θ,然后根据主题分布Θ产生主题z)的概率,主题z产生单词w的概率都不再是某两个确定的值,而是随机变量。
好比,我去一朋友家:
- 按照频率派的思想,我估计他在家的概率是1/2,不在家的概率也是1/2,是个定值。
- 而按照贝叶斯派的思想,他在家不在家的概率不再认为是个定值1/2,而是随机变量。比如按照我们的经验(比如当天周末),猜测他在家的概率是0.6,但这个0.6不是说就是完全确定的,也有可能是0.7。如此,贝叶斯派没法确切给出参数的确定值(0.3,0.4,0.6,0.7,0.8,0.9都有可能),但至少明白哪些取值(0.6,0.7,0.8,0.9)更有可能,哪些取值(0.3,0.4) 不太可能。进一步,贝叶斯估计中,参数的多个估计值服从一定的先验分布,而后根据实践获得的数据(例如周末不断跑他家),不断修正之前的参数估计,从先验分布慢慢过渡到后验分布。
4.3.2 LDA生成文档过程的进一步理解
在这个三维坐标轴所划分的空间里,每一个坐标点(p1,p2,p3)就对应着一个主题分布,且某一个点(p1,p2,p3)的大小表示3个主题z1、z2、z3出现的概率大小(因为各个主题出现的概率和为1,所以p1+p2+p3 = 1,且p1、p2、p3这3个点最大取值为1)。比如(p1,p2,p3) = (0.4,0.5,0.1)便对应着主题分布{ P(zi), i =1,2,3 } = {0.4,0.5,0.1}。
可以想象到,空间里有很多这样的点(p1,p2,p3),意味着有很多的主题分布可供选择,那dirichlet分布如何选择主题分布呢?把上面的斜三角形放倒,映射到底面的平面上,便得到如下所示的一些彩图(3个彩图中,每一个点对应一个主题分布,高度代表某个主题分布被dirichlet分布选中的概率,且选不同的![]() ,dirichlet 分布会偏向不同的主题分布):
,dirichlet 分布会偏向不同的主题分布):
![]()
4.3.3 pLSA跟LDA的概率图对比
- 假定语料库中共有M篇文章,每篇文章下的Topic的主题分布是一个从参数为
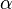 的Dirichlet先验分布中采样得到的Multinomial分布,每个Topic下的词分布是一个从参数为
的Dirichlet先验分布中采样得到的Multinomial分布,每个Topic下的词分布是一个从参数为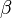 的Dirichlet先验分布中采样得到的Multinomial分布。
的Dirichlet先验分布中采样得到的Multinomial分布。 - 对于某篇文章中的第n个词,首先从该文章中出现的每个主题的Multinomial分布(主题分布)中选择或采样一个主题,然后再在这个主题对应的词的Multinomial分布(词分布)中选择或采样一个词。不断重复这个随机生成过程,直到M篇文章全部生成完成。
- 其中,
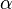 →θ→z 表示生成文档中的所有词对应的主题,显然
→θ→z 表示生成文档中的所有词对应的主题,显然 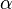 →θ 对应的是Dirichlet 分布,θ→z 对应的是 Multinomial 分布,所以整体是一个 Dirichlet-Multinomial 共轭结构,如下图所示:
→θ 对应的是Dirichlet 分布,θ→z 对应的是 Multinomial 分布,所以整体是一个 Dirichlet-Multinomial 共轭结构,如下图所示:
- 类似的,
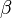 →φ→w,容易看出, 此时β→φ对应的是 Dirichlet 分布, φ→w 对应的是 Multinomial 分布, 所以整体也是一个Dirichlet-Multinomial 共轭结构,如下图所示:
→φ→w,容易看出, 此时β→φ对应的是 Dirichlet 分布, φ→w 对应的是 Multinomial 分布, 所以整体也是一个Dirichlet-Multinomial 共轭结构,如下图所示:
4.3.4 pLSA跟LDA参数估计方法的对比
- 在pLSA中,我们使用EM算法去估计“主题-词项”矩阵Φ(由
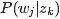 转换得到)和“文档-主题”矩阵Θ(由
转换得到)和“文档-主题”矩阵Θ(由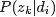 转换得到)这两个参数,而且这两参数都是个固定的值,只是未知,使用的思想其实就是极大似然估计MLE。
转换得到)这两个参数,而且这两参数都是个固定的值,只是未知,使用的思想其实就是极大似然估计MLE。 - 而在LDA中,估计Φ、Θ这两未知参数可以用变分(Variational inference)-EM算法,也可以用gibbs采样,前者的思想是最大后验估计MAP(MAP与MLE类似,都把未知参数当作固定的值),后者的思想是贝叶斯估计。贝叶斯估计是对MAP的扩展,但它与MAP有着本质的不同,即贝叶斯估计把待估计的参数看作是服从某种先验分布的随机变量。
- 关于贝叶斯估计再举个例子。假设中国的大学只有两种:理工科和文科,这两种学校数量的比例是1:1,其中,理工科男女比例7:1,文科男女比例1:7。某天你被外星人随机扔到一个校园,问你该学校可能的男女比例是多少?然后,你实际到该校园里逛了一圈,看到的5个人全是男的,这时候再次问你这个校园的男女比例是多少?
- 因为刚开始时,有先验知识,所以该学校的男女比例要么是7:1,要么是1:7,即P(比例为7:1) = 1/2,P(比例为1:7) = 1/2。
- 然后看到5个男生后重新估计男女比例,其实就是求P(比例7:1|5个男生)= ?,P(比例1:7|5个男生) = ?
- 用贝叶斯公式
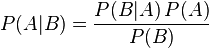 ,可得:P(比例7:1|5个男生) = P(比例7:1)*P(5个男生|比例7:1) / P(5个男生),P(5个男生)是5个男生的先验概率,与学校无关,所以是个常数;类似的,P(比例1:7|5个男生) = P((比例1:7)*P(5个男生|比例1:7)/P(5个男生)。
,可得:P(比例7:1|5个男生) = P(比例7:1)*P(5个男生|比例7:1) / P(5个男生),P(5个男生)是5个男生的先验概率,与学校无关,所以是个常数;类似的,P(比例1:7|5个男生) = P((比例1:7)*P(5个男生|比例1:7)/P(5个男生)。 - 最后将上述两个等式比一下,可得:P(比例7:1|5个男生)/P(比例1:7|5个男生) = {P((比例7:1)*P(5个男生|比例7:1)} / { P(比例1:7)*P(5个男生|比例1:7)}。
- 关于贝叶斯估计再举个例子。假设中国的大学只有两种:理工科和文科,这两种学校数量的比例是1:1,其中,理工科男女比例7:1,文科男女比例1:7。某天你被外星人随机扔到一个校园,问你该学校可能的男女比例是多少?然后,你实际到该校园里逛了一圈,看到的5个人全是男的,这时候再次问你这个校园的男女比例是多少?
4.3.5 LDA参数估计:Gibbs采样
理清了LDA中的物理过程,下面咱们来看下如何学习估计。
类似于pLSA,LDA的原始论文中是用的变分-EM算法估计未知参数,后来发现另一种估计LDA未知参数的方法更好,这种方法就是:Gibbs Sampling,有时叫Gibbs采样或Gibbs抽样,都一个意思。Gibbs抽样是马尔可夫链蒙特卡尔理论(MCMC)中用来获取一系列近似等于指定多维概率分布(比如2个或者多个随机变量的联合概率分布)观察样本的算法。殊途同归,目标一致,手段不一样而已。这也从侧面上再一次佐证,LDA跟pLSA并无本质区别,只是LDA在pLSA的基础上加了层贝叶斯框架,框架里的事情基本一样。
OK,给定一个文档集合,w是可以观察到的已知变量,![]() 和
和![]() 是根据经验给定的先验参数,其他的变量z,θ和φ都是未知的隐含变量,需要根据观察到的变量来学习估计的。根据LDA的图模型,可以写出所有变量的联合分布:
是根据经验给定的先验参数,其他的变量z,θ和φ都是未知的隐含变量,需要根据观察到的变量来学习估计的。根据LDA的图模型,可以写出所有变量的联合分布:
注:上述公式中及下文中,![]() 等价上文中定义的
等价上文中定义的![]() ,
,![]() 等价于上文中定义的
等价于上文中定义的![]() ,
,![]() 等价于上文中定义的
等价于上文中定义的![]() ,
,等价于上文中定义的
![]() 。
。
因为![]() 产生主题分布θ,主题分布θ确定具体主题,且
产生主题分布θ,主题分布θ确定具体主题,且![]() 产生词分布φ、词分布φ确定具体词,所以上述式子等价于下述式子所表达的联合概率分布
产生词分布φ、词分布φ确定具体词,所以上述式子等价于下述式子所表达的联合概率分布![]() :
:
其中,第一项因子![]() 表示的是根据确定的主题
表示的是根据确定的主题![]() 和词分布的先验分布参数
和词分布的先验分布参数![]() 采样词的过程,第二项因子
采样词的过程,第二项因子![]() 是根据主题分布的先验分布参数
是根据主题分布的先验分布参数![]() 采样主题的过程,这两项因子是需要计算的两个未知参数。
采样主题的过程,这两项因子是需要计算的两个未知参数。
由于这两个过程是独立的,所以下面可以分别处理,各个击破。
第一个因子![]() ,可以根据确定的主题
,可以根据确定的主题![]() 和从先验分布
和从先验分布![]() 取样得到的词分布Φ产生:
取样得到的词分布Φ产生:
由于样本中的词服从参数为主题![]() 的独立多项分布,这意味着可以把上面对词的乘积分解成分别对主题和对词的两层乘积:
的独立多项分布,这意味着可以把上面对词的乘积分解成分别对主题和对词的两层乘积:
其中,![]() 是词 t 在主题 k 中出现的次数。
是词 t 在主题 k 中出现的次数。
回到第一个因子上来。目标分布![]() 需要对词分布Φ积分,且结合我们之前在3.1节定义的Dirichlet 分布的归一化系数
需要对词分布Φ积分,且结合我们之前在3.1节定义的Dirichlet 分布的归一化系数![]() 的公式
的公式
可得:
这个结果可以看作K个Dirichlet-Multinomial模型的乘积。
现在开始求第二个因子![]() 。类似于
。类似于![]() 的步骤,先写出条件分布,然后分解成两部分的乘积:
的步骤,先写出条件分布,然后分解成两部分的乘积:
其中,![]() 表示的单词 i 所属的文档,
表示的单词 i 所属的文档,![]() 是主题 k 在文章 m 中出现的次数。
是主题 k 在文章 m 中出现的次数。
对主题分布Θ积分可得:
综合第一个因子和第二个因子的结果,得到![]() 的联合分布结果为:
的联合分布结果为:
“ 如果![]() ,同样可以证明有下述结论成立:
,同样可以证明有下述结论成立:
所以, 最终求解的Dirichlet 分布期望为:
5 读者微评
- @SiNZeRo:lda 如果用em就是 map估计了. lda本意是要去找后验分布 然后拿后验分布做bayesian分析. 比如theta的期望 . 而不是把先验作为正则化引入。最后一点gibbs sampling其实不是求解的过程 是去explore后验分布 去采样 用于求期望.
- @研究者July:好问题好建议
,这几天我陆续完善下!//@帅广应s:LDA这个东西该怎么用?可以用在哪些地方?还有就是Gibbs抽样的原理是什么?代码怎么实现?如果用EM来做,代码怎么实现? LDA模型的变形和优化有哪些?LDA不适用于解决哪类的问题?总之,不明白怎么用,参数怎么调优?
- @xiangnanhe:写的很好,4.1.3节中的那两个图很赞,非常直观的理解了LDA模型加了先验之后在学参数的时候要比PLSI更灵活;PLSI在学参数的过程中比较容易陷入local minimum然后overfitting。
- @asker2:无论是pLSA中,还是LDA中,主题分布和词分布本身是固定的存在,但都未知。pLSA跟LDA的区别在于,去探索这两个未知参数的方法或思想不一样。pLSA是求到一个能拟合文本最好的参数(分布),这个值就认为是真实的参数。但LDA认为,其实我们没法去完全求解出主题分布、词分布到底是什么参数,我们只能把它们当成随机变量,通过缩小其方差(变化度)来尽量让这个随机变量变得更“确切”。换言之,我们不再求主题分布、词分布的具体值,而是通过这些分布生成的观测值(即实际文本)来反推分布的参数的范围,即在什么范围比较可能,在什么范围不太可能。所以,其实这就是一种贝叶斯分析的思想,虽然无法给出真实值具体是多少,但可以按照经验给一个相对合理的真实值服从的先验分布,然后从先验出发求解其后验分布。
- ..
6 参考文献与推荐阅读
- Blei, David M.; Ng, Andrew Y.; Jordan, Michael I. Latent Dirichlet allocation(LDA原始论文):http://www.jmlr.org/papers/volume3/blei03a/blei03a.pdf。
- Blei. Probabilistic Topic Models:http://www.cs.princeton.edu/~blei/papers/Blei2012.pdf,一网友的翻译:http://www.cnblogs.com/siegfang/archive/2013/01/30/2882391.html;
- 一堆wikipedia,比如隐含狄利克雷分布LDA的wiki:http://zh.wikipedia.org/wiki/%E9%9A%90%E5%90%AB%E7%8B%84%E5%88%A9%E5%85%8B%E9%9B%B7%E5%88%86%E5%B8%83,狄利克雷分布的wiki:http://zh.wikipedia.org/wiki/%E7%8B%84%E5%88%A9%E5%85%8B%E9%9B%B7%E5%88%86%E5%B8%83;
- 从贝叶斯方法谈到贝叶斯网络 ;
- rickjin的LDA数学八卦(力荐,本文部分图片和公式来自于此文档)网页版:http://www.flickering.cn/tag/lda/,PDF版:http://emma.memect.com/t/9756da9a47744de993d8df13a26e04e38286c9bc1c5a0d2b259c4564c6613298/LDA;
- Thomas Hofmann.Probabilistic Latent Semantic Indexing(pLSA原始论文):http://cs.brown.edu/~th/papers/Hofmann-SIGIR99.pdf;
- Gregor Heinrich.Parameter estimation for text analysis(关于Gibbs 采样最精准细致的论述):http://www.arbylon.net/publications/text-est.pdf;
- Probabilistic latent semantic analysis (pLSA):http://blog.tomtung.com/2011/10/plsa/http://blog.tomtung.com/2011/10/plsa/。
- 《概率论与数理统计教程第二版 茆诗松等人著》,如果忘了相关统计分布,建议复习此书或此文第二部分;
- 机器学习班第11次课上,邹博讲EM & GMM的PPT:http://pan.baidu.com/s/1i3zgmzF;
- 机器学习班第12次课上,邹博讲主题模型LDA的PPT:http://pan.baidu.com/s/1jGghtQm;
- 主题模型之pLSA:http://blog.jqian.net/post/plsa.html;
- 主题模型之LDA:http://blog.jqian.net/post/lda.html;
- 搜索背后的奥秘——浅谈语义主题计算:http://www.semgle.com/search-engine-algorithms-mystery-behind-search-on-the-calculation-of-semantic-topic;
- LDA的EM推导:http://www.cnblogs.com/hebin/archive/2013/04/25/3043575.html;
- Machine Learning读书会第8期上,沈博讲主题模型的PPT:http://vdisk.weibo.com/s/zrFL6OXKgKMAf;
- Latent Dirichlet Allocation (LDA)- David M.Blei:http://www.xperseverance.net/blogs/2012/03/17/;
- 用GibbsLDA做Topic Modeling:http://weblab.com.cityu.edu.hk/blog/luheng/2011/06/24/%E7%94%A8gibbslda%E5%81%9Atopic-modeling/#comment-87;
- 主题模型在文本挖掘中的应用:http://net.pku.edu.cn/~zhaoxin/Topic-model-xin-zhao-wayne.pdf;
- 二项分布和多项分布,beta分布的对比:http://www.cnblogs.com/wybang/p/3206719.html;
- LDA简介:http://cos.name/2010/10/lda_topic_model/;
- LDA的相关论文、工具库:http://site.douban.com/204776/widget/notes/12599608/note/287085506/;
- 一个网友学习LDA的心得:http://www.xuwenhao.com/2011/03/20/suggestions-for-programmers-to-learn-lda/;
- http://blog.csdn.net/hxxiaopei/article/details/7617838;
- 主题模型LDA及其在微博推荐&广告算法中的应用:http://www.wbrecom.com/?p=136。