平衡二叉树（AVL树）

本文来自：https://blog.zhenlanghuo.top/2017/08/22/AVL%E5%B9%B3%E8%A1%A1%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%AE%9E%E7%8E%B0/

普通的二叉查找树在插入有序的数据的时候会退化为链表，查找的时间复杂度退化为O(n)。而平衡二叉树在插入数据的时候一直保持二叉树的平衡，从而保证查找的时间复杂度维持在O(logn)。

平衡二叉树的定义

一棵平衡二叉树是其每个结点的左子树和右子树的高度最多相差1的二叉查找树(空树的高度为-1)。

二叉树的高度——当前结点到叶子结点的最长路径

四种旋转的情况
若平衡二叉树种某个结点的左子树和右子树的高度相差大于1，该树就是失衡了，该结点称为失衡点，就要通过旋转来保持二叉树的平衡。

一共分四种情况导致结点失衡：

• 在结点的左孩子的左子树中插入数据（LL）
• 在结点的左孩子的右子树中插入数据（LR）
• 在结点的右孩子的左子树中插入数据（RL）
• 在结点的右孩子的右子树中插入数据（RR）

第1和4种情况是对称的，可用单旋来解决，而第2和3种情况也是对称的，要用双旋来解决。

LL型（左孩子的左子树）通过右旋解决

对于LL型的情况，要使用右旋来解决，将失衡点右旋到其左孩子的右孩子的位置，失衡点的左子树更新为其原来左孩子的右子树。


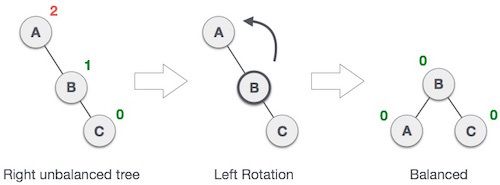
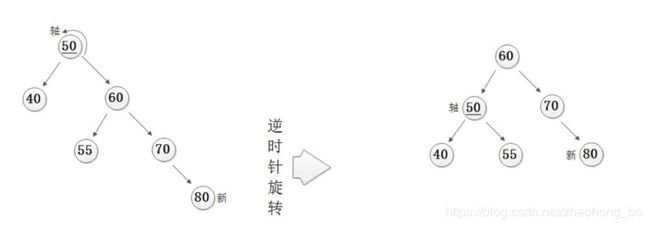
RR型（右孩子的右子树）通过左旋解决
对于RR型的情况，要使用左旋来解决，将失衡点左旋到其右孩子的左孩子的位置，失衡点的右子树更新为其原来右孩子的左子树。


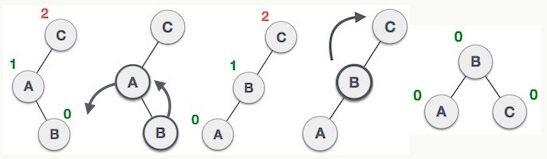
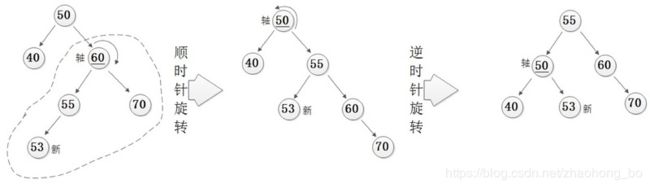
LR型（左孩子的右子树）通过先左旋再右旋解决
对于LR型的情况，要使用先对失衡点的左孩子进行左旋，然后再对失衡点进行右旋来解决。


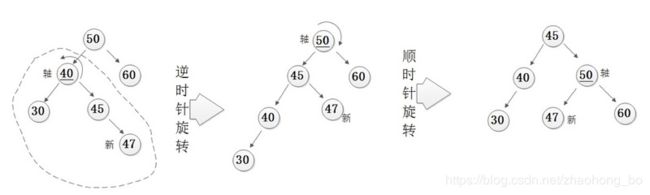
RL型（右孩子的左子树）通过先右旋再左旋解决
对于RL型的情况，要使用先对失衡点的右孩子进行右旋，然后再对失衡点进行左旋来解决。

3、代码实现

3.1 AVLNode

public class AVLNode<T extends Comparable<T>> {
	
	public AVLNode<T> left;
	
	public AVLNode<T> right;
	
	public T data;
	
	//当前结点的高度
	public int height;
	
	public AVLNode(T data) {
		this.data = data;
	}
	
}

AVLNode中一定要保存结点的高度，并在高度有变化的时候进行更新，我看过有一些简单的实现，在结点的数据结构中没有记录结点的高度，每次判断是否平衡的时候都要重新递归计算结点的高度，这样的做法效率很低

3.2 四种情况的旋转操作

  /**
 * 右旋操作（针对LL型的情况）
 * @param unbalance
 * @return
 */
public AVLNode<T> singleRotateRight(AVLNode<T> unbalance) {
	//失衡点的左孩子
	AVLNode<T> leftNode = unbalance.left;
	
	//将失衡点的左孩子更新为leftNode的右子树
	unbalance.left = leftNode.right;
	//失衡点右旋，变成leftNode的右孩子
	leftNode.right = unbalance;
	
	//更新leftNode和失衡点的高度
	unbalance.height = Math.max(height(unbalance.left),height(unbalance.right)) + 1;
	leftNode.height = Math.max(height(leftNode.left),unbalance.height) + 1;
	
	return leftNode;
}

/**
 * 左旋操作（针对RR型的情况）
 * @param unbalance
 * @return
 */
public AVLNode<T> singleRotateLeft(AVLNode<T> unbalance) {
	//失衡点的右孩子
	AVLNode<T> rightNode = unbalance.right;
	
	//将失衡点的右孩子更新为rightNode的左子树
	unbalance.right = rightNode.left;
	//失衡点左旋，变成rightNode的左孩子
	rightNode.left = unbalance;
	
	//更新rightNode和失衡点的高度
	unbalance.height = Math.max(height(unbalance.left),height(unbalance.right)) + 1;
	rightNode.height = Math.max(height(rightNode.right), unbalance.height) + 1;
	
	return rightNode;
}

/**
 * 先左旋再右旋操作（针对LR型的情况）
 * @param unbalance
 * @return
 */
public AVLNode<T> doubleRotateLeftRight(AVLNode<T> unbalance) {
	unbalance.left = singleRotateLeft(unbalance.left);
	return singleRotateRight(unbalance);
}

/**
 * 先右旋再左旋操作（针对RL型的情况）
 * @param unbalance
 * @return
 */
public AVLNode<T> doubleRotateRightLeft(AVLNode<T> unbalance) {
	unbalance.right = singleRotateRight(unbalance.right);
	return singleRotateLeft(unbalance);
}

旋转的操作的代码其实比较简单，按照着上边所描述的旋转的操作进行相应的结点左右孩子指针的更新就可以了

3.3 插入操作

 public int height() {
	return height(root);
}

public int height(AVLNode<T> node) {
	//空结点高度为-1;
	return node==null?-1:node.height;
}

/**
 * 插入方法
 * @param data
 */
public void insert(T data) {
	if (data==null){
           throw new RuntimeException("data can\'t not be null ");
       }
	this.root = insert(data, root);
}

/**
 * 插入操作
 * @param data
 * @param node
 * @return
 */
public AVLNode<T> insert(T data,AVLNode<T> node) {
	
	//node为null，表明已经找到插入的位置了，可以创建新结点了
	if(node==null) {
		node = new AVLNode<T>(data);
	}
	
	int comp = data.compareTo(node.data);
	
	//插入的值比当前node结点要小，因此要插入到结点的左子树，否则要插入到结点的右子树
	if(comp<0) {
		node.left = insert(data, node.left);
		
		//判断插入结点后，左右子树的高度差是否等于2，一旦都等于2，表明该结点为失衡点，就要开始旋转操作进行恢复平衡
		if(height(node.left)-height(node.right)==2) {
			//判断插入的数据是插入到失衡点左孩子的左子树还是右子树
			if(data.compareTo(node.left.data)<0) {
				//若是左子树，则是LL型
				node = singleRotateRight(node);
			}
			else {
				//若是右子树，则是LR型
				node = doubleRotateLeftRight(node);
			}
		}
	}
	else if(comp>0) {
		node.right = insert(data, node.right);
		
		//判断插入结点后，左右子树的高度差是否等于2，一旦都等于2，表明该结点为失衡点，就要开始旋转操作进行恢复平衡
		if(height(node.right)-height(node.left)==2) {
			//判断插入的数据是插入到失衡点左孩子的左子树还是右子树
			if(data.compareTo(node.right.data)<0) {
				//若是左子树，则是RL型
				node = doubleRotateRightLeft(node);
			}
			else {
				//若是右子树，则是RR型
				node = singleRotateLeft(node);
			}
		}
	}
	
	node.height = Math.max(height(node.left), height(node.right)) + 1;
	
	return node;
}

主要的思路就是利用查找树的性质，递归的找到数据要插入的位置，然后在递归返回的时候，更新结点的高度，并判断结点是否失衡了，一旦找到发现失衡点，就调用相应的旋转操作函数进行恢复。

3.4 删除操作

/**
 * 删除方法
 * @param data
 */
public void remove(T data) {
    if (data==null){
        throw new RuntimeException("data can\'t not be null ");
    }
    this.root=remove(data,root);
}

/**
 * 删除操作
 * @param data
 * @param p
 * @return
 */
private AVLNode<T> remove(T data,AVLNode<T> p){

    if(p ==null)
        return null;

    int result=data.compareTo(p.data);

    //从左子树查找需要删除的元素
    if(result<0){
        p.left=remove(data,p.left);

        //检测是否平衡
        if(height(p.right)-height(p.left)==2){
            AVLNode<T> currentNode=p.right;
            //判断需要那种旋转
            if(height(currentNode.right)>=height(currentNode.left)){
                //RR
                p=singleRotateLeft(p);
            }else{
                //RL
                p=doubleRotateRightLeft(p);
            }
        }

    }
    //从右子树查找需要删除的元素
    else if(result>0){
        p.right=remove(data,p.right);
        //检测是否平衡
        if(height(p.left)-height(p.right)==2){
            AVLNode<T> currentNode=p.left;
            //判断需要那种旋转
            if(height(currentNode.left)>=height(currentNode.right)){
                //LL
                p=singleRotateRight(p);
            }else{
                //LR
                p=doubleRotateLeftRight(p);
            }
        }
    }
    //已找到需要删除的元素,并且要删除的结点拥有两个子节点
    else if(p.right!=null&&p.left!=null){

        //寻找替换结点
        p.data=findMin(p.right).data;

        //移除用于替换的结点
        p.right = remove( p.data, p.right );
    }
    else {
        //只有一个孩子结点或者只是叶子结点的情况
        p=(p.left!=null)? p.left:p.right;
    }

    //更新高度值
    if(p!=null)
        p.height = Math.max( height( p.left ), height( p.right ) ) + 1;
    return p;
}

删除操作跟插入操作差不多，递归地找到要删除的数据的位置，然后利用查找树删除结点的方法来删除结点，在递归返回的时候更新结点的高度，并检查判断结点是否失衡了，一旦找到发现失衡点，就调用相应的旋转操作函数进行恢复。这里强调一下，插入操作只需要如果发现失衡点，只需要一次或两次旋转就可以恢复平衡了，而删除操作有可能多次发现失衡点，因此删除操作最多要旋转操作log(n)遍。

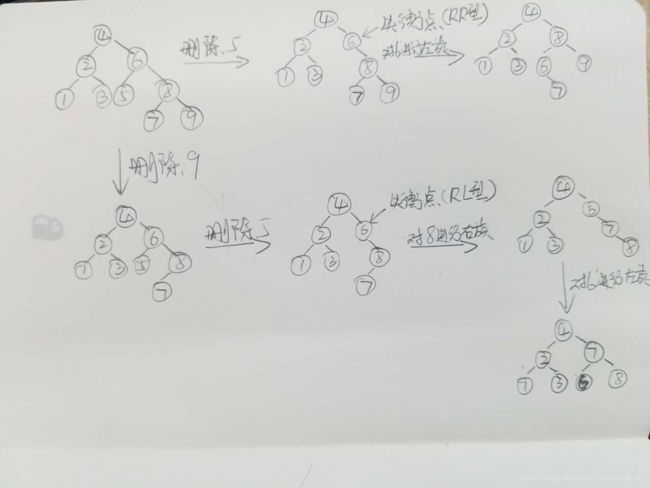
若删除的数据，是在失衡点的左子树，那么这个时候就判断一下失衡点的右孩子的左右子树的高度，若失衡点的右孩子的右子树高度大于等于左子树的高度，则该失衡点对应RR型，要对失衡点进行左旋操作；若右子树高度小于左子树，则对应RL型，要对失衡点的右孩子进行右旋操作，在对失衡点进行左旋操作。如下图的例子（用软件画图太麻烦了[捂脸]）

3.5 判断二叉树是否是平衡二叉树

3.5.1 递归法

public class Tree {

    static class TreeNode {
        int val;
        TreeNode right;
        TreeNode left;
        TreeNode(int x) {
            this.val = x;
        }
    }

    /**
     * 判断一棵二叉树是不是平衡二叉树
     * @param root
     * @return
     */
    public static boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        return isBalanced(root.left) && isBalanced(root.right) && Math.abs(getHeight(root.left) - getHeight(root.right))<2;
    }

    private static int getHeight(TreeNode root) {
        //获取二叉树的最大深度
        if(root != null) {
            int leftHeight = getHeight(root.left);
            int rightHeight = getHeight(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }else {
            return 0;
        }
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(12);
        root.left = new TreeNode(10);
        root.right = new TreeNode(13);
        root.left.right =new TreeNode(11);
        System.out.println(isBalanced(root));

    }
}

3.6 完整代码

代码地址