机器学习——马尔可夫模型及马尔可夫决策过程（MDP）

一、马尔可夫模型

1. 马尔可夫链

设表示随机变量X在离散时间t时刻的取值。若该变量随时间变化的转移概率仅依赖于它的当前值，即：

也就是时候状态转移概率指依赖于前一个状态，称这个变量为马尔可夫变量，其中 为随机变量X可能的状态，这个性质称为马尔可夫性质，具有马尔可夫性质的随机过程称为马尔可夫过程。

马尔可夫链是满足马尔可夫性质的随机过程，指在一段时间内随机变量X的取值序列（）满足上述性质

2、转移概率

马尔可夫链是通过转移概率定义的，转移概率指随机变量从一个时刻到下一个时刻，从状态转移到状态的概率：

记表示变量X在时刻t的取值为的概率，则随机变量X在时刻t+1的取值为的概率为：

假设状态的数目为n，则：

3 马尔可夫链的平稳分布

• 1.周期性：即经过有限次的状态转移，又回到了自身
• 1. 不可约：两个状态之间的转移

  马尔可夫模型如下所示：

可见状态之间没有转换概率，但是隐含态和可见态之间存在一个概率叫做输出概率。
上述概率转移公式就是表示模型中状态转移的情况。
如果一个马尔可夫过程既没有周期性，又不可约，则称为各态遍历的。

对于一个各态遍历的马尔可夫过程，无论初始值取何值，随着转移次数的增多，随机变量的取值分布最终都收敛到唯一的平稳分布：

其中为转移概率矩阵。

二、隐含马尔可夫模型(HMM)

HMM是关于时序的概率模型，描述由一个隐藏的马尔可夫链生成的不客观状态随机序列，再由各个状态生成观测的随机序列的过程，如下所示：

1. HMM的定义

HMM的参数：
Q 是所有可能的状态的集合, 其中 N 是可能的状态数;
V 是所有可能的观测的集合, 其中 M 是可能的观测数;

I 是长度为 TT 的状态序列; O 是对应的观测序列:

隐马尔科夫也比马尔科夫多了一个假设，即输出仅与当前状态有关，可以用如下公式表示：

P(O1,O2,…,Ot|S1,S2,…,St)=P(O1|S1)P(O2|S2)…*P(Ot|St)

其中，O1,O2,…,Ot为从时刻1到时刻t的观测状态序列，S1,S2,…,St则为隐藏状态序列。

HMM的三要素：
HMM由初始概率分布 ππ (向量)、状态转移概率分布 A(矩阵) 以及观测概率分布 B (矩阵) 确定. π 和 A 决定状态序列, BB 决定观测序列。因此, HMM可以用三元符号表示, 称为HMM的三要素:

A是状态转移矩阵：

其中, 是在时刻 t 处于状态 的条件下时刻 t+1 转移到状态 的概率:

B是观测转移概率矩阵：

其中, 是在时刻 t 处于状态 qi 的条件下生成观测 的概率:

π 是初始状态概率向量:

其中是时刻t=1处于状态的概率：

HMM增加了一个假设：
齐次马尔可夫性假设 任意时刻 t 的状态, 只依赖于其前一刻的状态, 与其他时刻的状态及观测无关, 也与时刻 t 无关.

观测独立性假设 任何时刻的观测只依赖于该时刻的马尔科夫链状态. 与其他观测及状态无关.

概率计算问题：
1.计算模型λ下观测序列O出现的概率P(O|λ)
2.估计模型的参数，使得该模型下观测序列P(O|λ)最大
3.已知模型 λ=(A,B,π) , 和观测序列 O={o1,o2,⋯,oT}
求给定观测序列条件概率 P(I∣O,λ)P(I∣O,λ) 最大的状态序列

2、直接计算

状态的概率

对固定的状态序列 ,观测序列 的概率是:

O 和 I 同时出现的联合概率:

对所有可能的状态序列I求和,得到观测序列O的概率：

此外还有前向算法，及后向算法。

参考 ：https://clyyuanzi.gitbooks.io/julymlnotes/content/hmm.html

三、马尔可夫决策过程（MDP）

MDP也具有马尔可夫性，与上面不同的是，MDP考虑了动作，即系统的下个状态不仅和当前的状态有关，也与当前采取的动作有关。比如下棋，当我们在某个局面（状态s）走了一步（动作a），这是对手的选择（导致下个状态s’）我们不确定，但是他的选择只与状态s和动作a有关，而与之前的状态和动作无关。

1 、 马尔可夫决策过程

一个马尔可夫决策过程由一个四元组构成M = (S, A, Psa, R)

S: 表示状态集(states)，有s∈S，si表示第i步的状态。
A:表示一组动作(actions)，有a∈A，ai表示第i步的动作。
Psa: 表示状态转移概率。Psa 表示的是在当前s ∈ S状态下，经过a ∈ A作用后，会转移到的其他状态的概率分布情况。比如，在状态s下执行动作a，转移到s’的概率可以表示为p(s’|s,a)。
R: S×A⟼ℝ ，R是回报函数(reward function)。有些回报函数状态S的函数，可以简化为R: S⟼ℝ。如果一组(s,a)转移到了下个状态s’，那么回报函数可记为r(s’|s, a)。如果(s,a)对应的下个状态s’是唯一的，那么回报函数也可以记为r(s,a)。

MDP 的动态过程如下：某个智能体(agent)的初始状态为s0，然后从 A 中挑选一个动作a0执行，执行后，agent 按Psa概率随机转移到了下一个s1状态，s1∈ Ps0a0。然后再执行一个动作a1，就转移到了s2，接下来再执行a2…，我们可以用下面的图表示状态转移的过程。

如果回报r是根据状态s和动作a得到的，则MDP还可以表示成下图：

2、 值函数（value function ）
上篇我们提到增强学习学到的是一个从环境状态到动作的映射（即行为策略），记为策略π: S→A。而增强学习往往又具有延迟回报的特点: 如果在第n步输掉了棋，那么只有状态sn和动作an获得了立即回报r(sn,an)=-1，前面的所有状态立即回报均为0。所以对于之前的任意状态s和动作a，立即回报函数r(s,a)无法说明策略的好坏。因而需要定义值函数(value function，又叫效用函数)来表明当前状态下策略π的长期影响。

用Vπ(s)表示策略π下，状态s的值函数。ri表示未来第i步的立即回报，常见的值函数有以下三种：

a)
b)
c)

其中：

a)是采用策略π的情况下未来有限h步的期望立即回报总和；

b)是采用策略π的情况下期望的平均回报；

c)是值函数最常见的形式，式中γ∈[0,1]称为折合因子，表明了未来的回报相对于当前回报的重要程度。特别的，γ=0时，相当于只考虑立即不考虑长期回报，γ=1时，将长期回报和立即回报看得同等重要。接下来我们只讨论第三种形式，
现在将值函数的第三种形式展开，其中ri表示未来第i步回报，s’表示下一步状态，则有：

给定策略π和初始状态s，则动作a=π(s)，下个时刻将以概率p(s’|s,a)转向下个状态s’，那么上式的期望可以拆开，可以重写为：

上面提到的值函数称为状态值函数(state value function)，需要注意的是，在Vπ(s)中，π和初始状态s是我们给定的，而初始动作a是由策略π和状态s决定的，即a=π(s)。

定义动作值函数(action value functionQ函数)如下：

给定当前状态s和当前动作a，在未来遵循策略π，那么系统将以概率p(s’|s,a)转向下个状态s’，上式可以重写为：

在Qπ(s,a)中，不仅策略π和初始状态s是我们给定的，当前的动作a也是我们给定的，这是Qπ(s,a)和Vπ(a)的主要区别。

知道值函数的概念后，一个MDP的最优策略可以由下式表示：

即我们寻找的是在任意初始条件s下，能够最大化值函数的策略π*。

1. 值函数与Q函数计算的例子

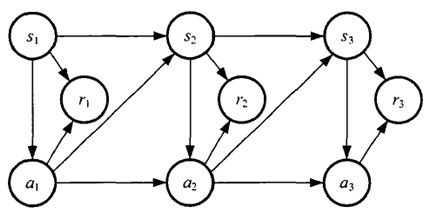
上面的概念可能描述得不够清晰，接下来我们实际计算一下，如图所示是一个格子世界，我们假设agent从左下角的start点出发，右上角为目标位置，称为吸收状态(Absorbing state)，对于进入吸收态的动作，我们给予立即回报100，对其他动作则给予0回报，折合因子γ的值我们选择0.9。

为了方便描述，记第i行，第j列的状态为sij, 在每个状态，有四种上下左右四种可选的动作，分别记为au,ad,al,ar。（up，down，left，right首字母），并认为状态按动作a选择的方向转移的概率为1。

1.由于状态转移概率是1，每组(s,a)对应了唯一的s’。回报函数r(s’|s,a)可以简记为r(s,a)

如下所示，每个格子代表一个状态s，箭头则代表动作a，旁边的数字代表立即回报，可以看到只有进入目标位置的动作获得了回报100，其他动作都获得了0回报。　即r(s_12,ar_) = r(s_23,a_u) =100。

1. 一个策略π如图所示：

   

2. 值函数Vπ(s)如下所示

根据Vπ的表达式，立即回报，和策略π，有

Vπ(s12) = r(s12,ar) = r(s13|s12,ar) = 100

Vπ(s11)= r(s11,ar)+γ*Vπ(s12) = 0+0.9*100 = 90

Vπ(s23) = r(s23,au) = 100

Vπ(s22)= r(s22,ar)+γ*Vπ(s23) = 90

Vπ(s21)= r(s21,ar)+γ*Vπ(s22) = 81

1. Q(s,a)值如下所示

有了策略π和立即回报函数r(s,a), Qπ(s,a)如何得到的呢？

对s11计算Q函数（用到了上面Vπ的结果）如下：

Qπ(s11,ar)=r(s11,ar)+ γ *Vπ(s12) =0+0.9*100 = 90

Qπ(s11,ad)=r(s11,ad)+ γ *Vπ(s21) = 72