特征向量和分类方法

数学建模

2000年A题 DNA序列分类

​ 2000 年 6 月，人类基因组计划中 DNA 全序列草图完成，预计 2001 年可以完成精确的全序列图，此后人类将拥有一本记录着自身生老病死及遗传进化的全部信息的“天书”。这本大自然写成的“天书”是由 4 个字符 A，T，C，G 按一定顺序排成的长约 30 亿的序列，其中没有“断句”也没有标点符号，除了这 4 个字符表示 4 种碱基以外，人们对它包含的“内容”知之甚少，难以读懂。破译这部世界上最巨量信息的“天书”是二十一世纪最重要的任务之一。在这个目标中，研究 DNA 全序列具有什么结构，由这 4 个字符排成的看似随机的序列中隐藏着什么规律，又是解读这部天书的基础，是生物信息学（Bioinformatics）最重要的课题之一。

​ 虽然人类对这部“天书”知之甚少，但也发现了 DNA 序列中的一些规律性和结构。例如，在全序列中有一些是用于编码蛋白质的序列片段，即由这 4 个字符组成的 64 种不同的 3 字符串，其中大多数用于编码构成蛋白质的 20 种氨基酸。又例如，在不用于编码蛋白质的序列片段中，A和 T 的含量特别多些，于是以某些碱基特别丰富作为特征去研究 DNA 序列的结构也取得了一些结果。此外，利用统计的方法还发现序列的某些片段之间具有相关性，等等。这些发现让人们相信，DNA 序列中存在着局部的和全局性的结构，充分发掘序列的结构对理解 DNA 全序列是十分有意义的。目前在这项研究中最普通的思想是省略序列的某些细节，突出特征，然后将其表示成适当的数学对象。这种被称为粗粒化和模型化的方法往往有助于研究规律性和结构。 作为研究 DNA 序列的结构的尝试，提出以下对序列集合进行分类的问题：

1）下面有 20 个已知类别的人工制造的序列，其中序列标号 1—10 为 A 类，11-20 为 B 类。

​ 请从中提取特征，构造分类方法，并用这些已知类别的序列，衡量你的方法是否足够好。然后用

​ 你认为满意的方法，对另外 20 个未标明类别的人工序列（标号 21—40）进行分类，把结果用序号（按从小到大的顺序）标明它们的类别（无法分类的不写入）： A 类 ； B 类 。 请详细描述你的方法，给出计算程序。如果你部分地使用了现成的分类方法，也要将方法称准确注明。

​ 这 40 个序列放在如下地址的网页上，用数据文件 Art-model-data 标识，供下载：

网易网址：www.163.com 教育频道 在线试题；

教育网： www.cbi.pku.edu.cn News mcm2000

教育网： www.csiam.edu.cn/mcm

[注] 目前这些网站上不一定还保存有该文件，这里将该文件的内容附于本题后。

2）在同样网址的数据文件 Nat-model-data 中给出了 182 个自然 DNA 序列，它们都较长。

用你的分类方法对它们进行分类，像 1）一样地给出分类结果。

提示：衡量分类方法优劣的标准是分类的正确率，构造分类方法有许多途径，例如提取序

列的某些特征，给出它们的数学表示：几何空间或向量空间的元素等，然后再选择或构造适合这

种数学表示的分类方法；又例如构造概率统计模型，然后用统计方法分类等。

（北京工业大学孟大志提供）

[附]数据文件 Art-model-data 的内容如下：

附录 1：已知类别的序列（用于提取特征及检验方法）

A 类 10 个序列：

>aggcacggaaaaacgggaataacggaggaggacttggcacggcattacacggaggacgaggtaaaggaggcttgtctac

ggccggaagtgaagggggatatgaccgcttggaattgtctg

>cggaggacaaacgggatggcggtattggaggtggcggactgttcggggaattattcggtttaaacgggacaaggaaggc

ggctggaacaaccggacggtggcagcaaaggaacggacacg

>gggacggatacggattctggccacggacggaaaggaggacacggcggacatacacggcggcaacggacggaacggagga

aggagggcggcaatcggtacggaggcggcggacggacggag

>atggataacggaaacaaaccagacaaacttcggtagaaatacagaagcttagatgcatatgttttttaaataaaatttg

tattattatggtatcataaaaaaaggttgcgagataacata

>cggctggcggacaacggactggcggattccaaaaacggaggaggcggacggaggctacaccaccgtttcggcggaaagg

cggagggctggcaggaggctcattacggggagcggaggcgg

>atggaaaattttcggaaaggcggcaggcaggaggcaaaggcggaaaggaaggaaacggcggatatttcggaagtggata

ttaggagggcggaataaaggaacggcggcacaaaggaggcg

>atgggattattgaatggcggaggaagatccggaataaaatatggcggaaagaacttgttttcggaaatggaaaaaggac

taggaatcggcggcaggaaggatatggaggcggaaggacgg

>atggccgatcggcttaggctggaaggaacaaataggcggaattaaggaaggcgttctcgcttttcgacaaggaggcgga

ccataggaggcggattaggaacggttatgaggaggactcgg

>atggcggaaaaaggaaatgtttggcatcggcgggctccggcaactggaggttcggccatggaggcgaaaatcgtgggcg

gcggcagcgctggccggagtttgaggagcgcggcacaatgt

>tggccgcggaggggcccgtcgggcgcggatttctacaagggcttcctgttaaggaggtggcatccaggcgtcgcacgct

cggcgcggcaggaggcacgcgggaaaaaacggggaggcggt

B 类 10 个序列：

>gttagatttaacgttttttatggaatttatggaattataaatttaaaaatttatattttttaggtaagtaatccaacgt

ttttattactttttaaaattaaatatttatttaaaatccag

>gtttaattactttatcatttaatttaggttttaattttaaatttaatttaggtaagatgaatttggttttttttaaggt

agttatttaattatcgttaaggaaagttaaaatctaagatt

>gtattacaggcagaccttatttaggttattattattatttggattttttttttttttttttttaagttaaccgaattat

tttctttaaagacgttacttaatgtcaatgctttatgcagg

>gttagtcttttttagattaaattattagattatgcagtttttttacataagaaaatttttttttcggagttcatattct

aatctgtctttattaaatcttagagatattatccgttaatt

>gtattatatttttttatttttattattttagaatataatttgaggtatgtgtttaaaaaaaattttttttttttttttt

ttttttttttttttaaaatttataaatttaaattttaaact

>gttatttttaaatttaattttaattttaaaatacaaaatttttactttctaaaattggtctctggatcgataatgtaaa

cttattgaatctatagaattacattattgattttttccaga

>gtatgtctatttcacggaagaatgcaccactatatgatttgaaattatctatggctaaaaaccctcagtaaaatcaatc

cctaaacccttaaaaaacggcggcctatcccgtcagtcgag

>gttaattatttattccttacgggcaattaattatttattacggttttatttacaattttttttttttgtcctatagaga

aattacttacaaaacgttattttacatacttattttttgtc

>gttacattatttattattatccgttatcgataattttttacctcttttttcgctgagtttttattcttactttttttct

tctttatataggatctcatttaatatcttaatttttcttag

>gtatttaactctctttactttttttttcactctctacattttcatcttctaaaactgtttgatttaaacttttgtttct

ttaaggattttttttacttatcctctgttatgtttatttag

附录 2： 测试集（人工制造）

1:

tttagctcagtccagctagctagtttacaatttcgacaccagtttcgcaccatcttaaatttcgatccgtaccgtaatttagcttagatttggatttaaaggattt

agattgacc

2:

tttagtacagtagctcagtccaagaacgatgtttaccgtaacdgtqacgtaccgtacgctaccgttaccggattccggaaagccgattaaggaccgatc

gaaaggga

3:

cgggcggatttaggccgacggggacccgggattcgggacccgaggaaattcccggattaaggtttagcttcccgggatttagggcccggatggctg

ggacccgc

4:

tttagctagctactttagctatttttagtagctagccagcctttaaggctagctttagctagcattgttctttattgggacccaagttcgacttttacgatttagtt

ttgaccgta

5:

gaccaaaggtgggctttagggacccgatgctttagtcgcagctggaccagttccccagggtattaggcaaaagctgacgggcaattgcaatttaggct

taggccag

6:

gatttactttagcatttttagctgacgttagcaagcattagctttagccaatttcgcatttgccagtttcgcagctcagttttaacgcgggatctttagcttcaa

gctttttacg

7:

ggattcggatttacccggggattggcggaacgggacctttaggtcgggacccattaggagtaaatgccaaaggacgctggtttagccagtccg5tta

aggcttagg

8:

tccttagatttcagttactatatttgacttacagtctttgagatttcccttacgattttgacttaaaatttagacgttagggcttatcagttatggattaatttagctt

attttcgaga

9:

ggccaattccggtaggaaggtgatggcccgggggttcccgggaggatttaggctgacgggccggccatttcggtttagggagggccgggacgcgt

tagggacg

10:

cgctaagcagctcaagctcagtcagtcacgtttgccaagtcagtaatttgccaaagttaaccgttagctgacgctgaacgctaaacagtattagctgatg

actcgtacg

11:

ttaaggacttaggctttagcagttactttagtttagttccaagctacgtttacgggaccagatgctagctagcaatttattatccgtattaggcttaccgtagg

tttagcggt

12:

tgctaccgggcagtctttaacgtagctaccgtttagtttgggcccagccttgcggtgtttcggattaaattcgttgtcagtcgctctrtgggtttagtcattcc

caaaaggt

13:

cagttagctgaatcgtttagccatttgacgtaaacatgattttacgtacgtaaattttagccctgacgtttagctaggaatttatgctgacgtagcgatcgac

tttagcacc

14:

cggttagggcaaaggttggatttcgacccagggggaaagcccgggacccgaacccagggctttagcgtaggctgacgctaggcttaggttggaac

ccggaaag

15:

gcggaagggcgtaggttthgggatgcttagccgtaggctagctttcgacacgatcgattcgcaccacaggataaaagttaagggaccggtaagtcg

cggtagccg

16:

ctagctacgaacgctttaggcgcccccgggagtagtcgttaccgttagtatagcagtcgcagtcgcaattcgcaaaagtccccagctttagccccaga

gtcgacgct

17:

gggatgctgacgctggttagctttaggcttagcgtagctttagggccccagtctgcaggaaatgcccaaaggaggcccaccgggtagatgccasagt

gcaccgta

18:

aacttttagggcatttccagttttacgggttattttcccagttaaactttgcaccattttacgtgttacgatttacgtataatttgaccttattttggacactttagtt

tgggttacc

19:

ttagggccaagtccdcgaggcaahggaattctgatccaagtccaatcacgtacagtccaagtcaccgtttgcagctaccgtttaccgtacgttgcaagt

caaatccat

20:

ccattagggtttatttacctgtttattttttcccgagaccttaggtttaccgtactttttaacggtttacctttgaaatttttggactagcttaccctggatttaacg

gccagtttgt

欧式距离和马氏距离

欧式距离和马氏距离

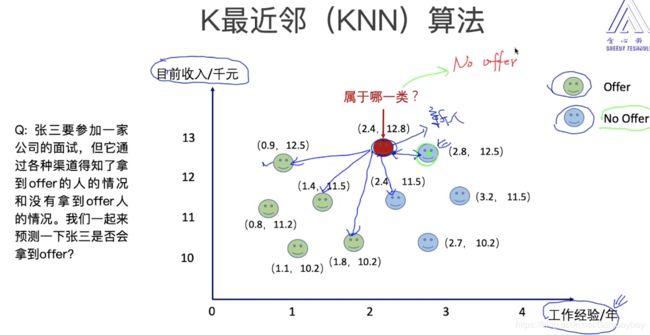
1.KNN算法介绍

KNN 是什么？

KNN(K-Nearest Neighbor)是最简单的机器学习算法之一，可以用于分类和回归，是一种监督学习算法。它的思路是这样，如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。也就是说，该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

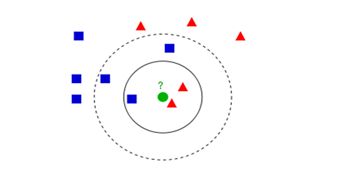
KNN用于分类
如上图所示，图中的正方形和三角形是打好了label的数据，分别代表不同的标签，那个绿色的圆形是我们待分类的数据。
如果选K=3，那么离绿色点最近K个点中有2个三角形和1个正方形，这3个点投票，三角形的比例占2/3，于是绿色的这个待分类点属于三角形类别。
如果选K=5，那么离绿色点最近K个点中有2个三角形和3个正方形，这5个点投票，蓝色的比例占3/5，于是绿色的这个待分类点属于正方形类别。

从上述例子看到，KNN本质是基于一种数据统计的方法，其实很多机器学习算法也是基于数据统计的。同时， KNN是一种instance-based learning，属于lazy learning， 即它没有明显的前期训练过程，而是程序开始运行时，把数据集加载到内存后，就可以直接开始分类。其中，每次判断一个未知的样本点时，就在该样本点附近找K个最近的点进行投票，这就是KNN中K的意义，通常K是不大于20的奇数。

KNN分类算法的计算过程：
1）计算待分类点与已知类别的点之间的距离
2）按照距离递增次序排序
3）选取与待分类点距离最小的K个点
4）确定前K个点所在类别的出现次数
5）返回前K个点出现次数最高的类别作为待分类点的预测分类

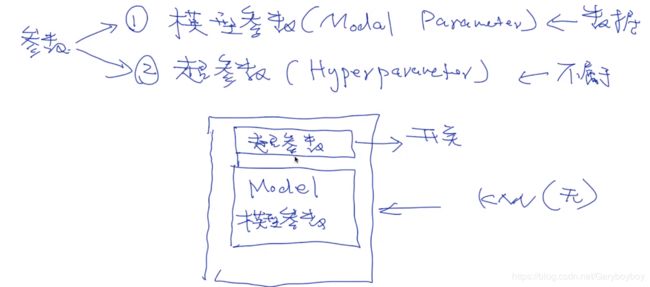
KNN算法要注意什么问题？
参数分为：模型参数和超参数
超参数：就相当于一个开关：告诉模型启用不同的训练方式；

（1）把一个物体表示成向量/矩阵；
（2）标记号每个物体的标签；
（2）计算两个物体之间的距离/相似度；距离度量，特征空间中样本点的距离是样本点间相似程度的反映
（3）选择合适的 K
其中，K值的选择和设置距离度量是最应该注意的几个问题;

代码实现：

1. 调用KNN函数来实现分类¶

数据采用的是经典的iris数据，是三分类问题

# 读取相应的库
from sklearn import datasets   # 使用sklearn 自带的数据集；
from sklearn.model_selection import train_test_split  # 把数据分为训练 和  测试数据
from sklearn.neighbors import KNeighborsClassifier
import numpy as np

# 读取数据 X, y
iris = datasets.load_iris()   # UCI dataset；3类描述；
X = iris.data  #特征：矩阵： N*D  N：#OF
y = iris.target   #label ：标签（0，1，2），向量；
print (X, y)
-------------------------------------------------------
[[ 5.1  3.5  1.4  0.2]
 [ 4.9  3.   1.4  0.2]
 [ 4.7  3.2  1.3  0.2]
 [ 4.6  3.1  1.5  0.2]
 [ 5.   3.6  1.4  0.2]
 [ 5.4  3.9  1.7  0.4]
 [ 4.6  3.4  1.4  0.3]
 [ 5.   3.4  1.5  0.2]
 [ 4.4  2.9  1.4  0.2]
 [ 4.9  3.1  1.5  0.1]
......

# 把数据分成训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2003)

# 构建KNN模型， K值为3、 并做训练
clf = KNeighborsClassifier(n_neighbors=3)  #指定K值
clf.fit(X_train, y_train)     #训练

# 计算准确率
from sklearn.metrics import accuracy_score
correct = np.count_nonzero((clf.predict(X_test)==y_test)==True)
#accuracy_score(y_test, clf.predict(X_test))
print ("Accuracy is: %.3f" %(correct/len(X_test)))
------------------------------------
Accuracy is: 0.921

2. 从零开始自己写一个KNN算法

from sklearn import datasets
from collections import Counter  # 为了做投票
from sklearn.model_selection import train_test_split   
import numpy as np

# 导入iris数据
iris = datasets.load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2003)

def euc_dis(instance1, instance2):
    """
    计算两个样本instance1和instance2之间的欧式距离
    instance1: 第一个样本， array型
    instance2: 第二个样本， array型
    """
    # TODO
    dist = np.sqrt(sum((instance1 - instance2)**2))
    return dist
    
 
def knn_classify(X, y, testInstance, k):
    """
    给定一个测试数据testInstance, 通过KNN算法来预测它的标签。 
    X: 训练数据的特征
    y: 训练数据的标签
    testInstance: 测试数据，这里假定一个测试数据 array型
    k: 选择多少个neighbors? 
    """
    # TODO  返回testInstance的预测标签 = {0,1,2}
    distances = [euc_dis(x, testInstance) for x in X]
    kneighbors = np.argsort(distances)[:k]
    count = Counter(y[kneighbors])
    return count.most_common()[0][0]

# 预测结果；
predictions = [knn_classify(X_train, y_train, data, 3) for data in X_test]
correct = np.count_nonzero((predictions==y_test)==True)
#accuracy_score(y_test, clf.predict(X_test))
print ("Accuracy is: %.3f" %(correct/len(X_test)))
-------------------------------------------------------------
Accuracy is: 0.921

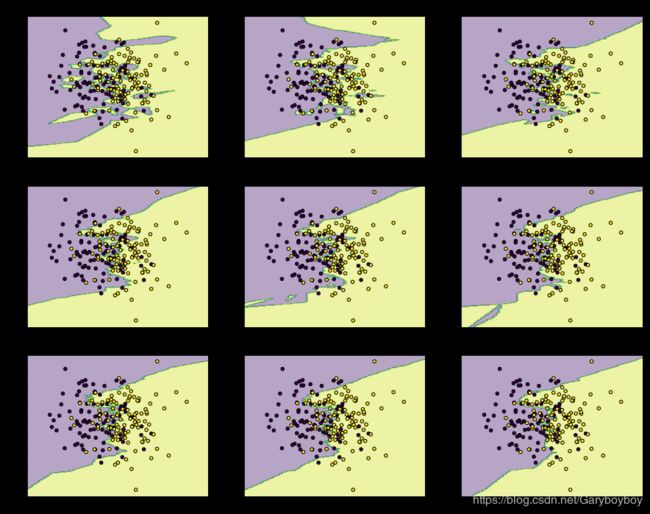
3. KNN的决策边界

import matplotlib.pyplot as plt
import numpy as np
from itertools import product
from sklearn.neighbors import KNeighborsClassifier

# 生成一些随机样本
n_points = 100
X1 = np.random.multivariate_normal([1,50], [[1,0],[0,10]], n_points)
X2 = np.random.multivariate_normal([2,50], [[1,0],[0,10]], n_points)
X = np.concatenate([X1,X2])
y = np.array([0]*n_points + [1]*n_points)
print (X.shape, y.shape)

# KNN模型的训练过程
clfs = []
neighbors = [1,3,5,9,11,13,15,17,19]
for i in range(len(neighbors)):
    clfs.append(KNeighborsClassifier(n_neighbors=neighbors[i]).fit(X,y))

# 可视化结果
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
                     np.arange(y_min, y_max, 0.1))

f, axarr = plt.subplots(3,3, sharex='col', sharey='row', figsize=(15, 12))
for idx, clf, tt in zip(product([0, 1, 2], [0, 1, 2]),
                        clfs,
                        ['KNN (k=%d)'%k for k in neighbors]):
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    axarr[idx[0], idx[1]].contourf(xx, yy, Z, alpha=0.4)
    axarr[idx[0], idx[1]].scatter(X[:, 0], X[:, 1], c=y,
                                  s=20, edgecolor='k')
    axarr[idx[0], idx[1]].set_title(tt)
    
plt.show()

Fisher分类

Fisher分类matlab实现

Bayes判别法

Bayes判别法

神经网络

粒子群优化RBF神经网络的DNA序列分类