红黑树---学习笔记(云课堂)

目录

1、使用场景

2、定义

    2.1、二叉查找树

3、性质

4、红黑树自平衡

    4.1、最小单元

    4.2、原子操作

    4.2.1、变色

    4.2.2、左旋

    4.2.3、右旋

    4.2.4、左旋、右旋、插入时的自平衡代码

 5、红黑树的查找操作

6、红黑树新增

    6.1、4中情况

    6.2、整体口诀

    6.2.1、情况1

    6.2.3、情况3

    6.2.4、情况4---CPG三点一线

    6.2.5、情况4---CPG三角关系

7、二叉树的平衡因子BF

8、AVL树

    8.1、定义性质

    8.2、自平衡

    8.2.1、第一步

    8.2.2、第二步

    8.2.3、第三步

---

1、使用场景

    1、JDK TreeSet、TreeMap、JDK1.8 HashMap
    2、Java NIO编程Epoll底层数据结构使用了红黑树
    3、c++红黑树广泛的使用在STL中

2、定义

    红黑树是一种含有红黑节点并能自平衡的二叉查找树。

红黑树：就是保证树相对平衡(黑色完美平衡)

    2.1、二叉查找树

    若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
    若右子树不空，则右子树上所有节点的值均大于它的根节点的值；

3、性质

（1）每个节点要么是黑色，要么是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色

 NIL节点：值为NULL，是不存在的，虚拟出来的

                  便于其他性质描述更加简洁、对自平衡有一定的作用
（4）每个红色节点的两个子节点一定都是黑色。
（5）任意节点到每个叶子节点的路径都包含数量相同的黑节点。

完美平衡：从根节点到叶子节点，最长深度，不超过最短深度的2倍。

黑色完美平衡：任意节点到每个叶子节点的路径都包含数量相同的黑节点

红黑树不是完美平衡二叉查找树，是一个相对平衡(黑色完美平衡)二叉查找树。

左斜树、右斜树，是将树退化成了链表

4、红黑树自平衡

    4.1、最小单元

祖孙三代(CPGU)

红黑树的自平衡每次只考虑CPGU三代即可，其余部分无需考虑

G：祖父Grandfather；P：父母Parents；U：叔叔Uncle

B：兄弟Brother；C：当前新增节点Current；R：根节点root

    4.2、原子操作

1、操作包括：变色、旋转

2、旋转又分为：左旋、右旋，旋转要有：圆心、方向。

左旋：逆时针；右旋：顺时针

3、旋转节点围绕子节点旋转（子节点为圆心）

    4.2.1、变色

由红色变为黑色，或由黑色变为红色

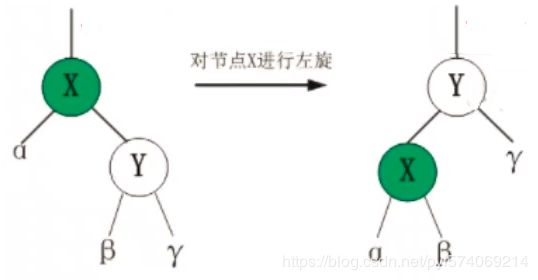
    4.2.2、左旋

旋转节点绕圆心逆时针旋转。旋转节点一定是父节点、圆心一定是子节点。【父母围着子女转】

基于最短路径：来确定旋转方向【父节点被旋转到正确位置(旋转后所在位置)，所需的最短路径】

    4.2.3、右旋

旋转节点绕圆心顺时针旋转。旋转节点一定是父节点、圆心一定是子节点。【父母围着子女转】

    4.2.4、左旋、右旋、插入时的自平衡代码

/**
 * 红黑树
 *
 * @createTime 2020年04月17日 10:16.
 */
public class RedBlackTree {
    private Node root;

    /**
     * 添加节点时：自平衡
     *
     * @param current
     */
    public void addSelfBalance(Node current) {
        Node parent;
        Node grandfather;
        Node uncle;
        //父节点不为空，并且父节点是红色
        while ((parent = current.getParent()) != null && parent.isColor()) {
            grandfather = parent.getParent();
            if (grandfather.getLeftChild() == parent) {
                uncle = grandfather.getRightChild();
                if (uncle != null) {
                    //TODO 情况1：当前节点的父节点和叔叔节点都是红色
                    if (uncle.isColor()) {
                        //变色
                        parent.setColor(false);
                        uncle.setColor(false);
                        grandfather.setColor(true);
                        current = grandfather;
                        continue;
                    } else {
                        if (current == parent.getRightChild()) {
                            //TODO 情况2：当前节点的父节点是红色，叔叔节点是黑色，且当前节点是父节点的右子节点
                            leftRotate(parent);//父节点围着当前节点左旋
                            //左旋后，父节点与当前节点互换
                            Node temp = parent;
                            parent = current;
                            current = temp;
                        }
                        //TODO 情况3：当前节点的父节点是红色，叔叔是黑色，且当前节点是父节点的左子节点
                        parent.setColor(false);
                        grandfather.setColor(true);
                        rightRotate(grandfather);
                    }
                }
            } else {
                uncle = grandfather.getLeftChild();
                //TODO 情况1：当前节点的父节点和叔叔节点都是红色
                if (uncle != null) {
                    if (uncle.isColor()) {
                        //变色
                        parent.setColor(false);
                        uncle.setColor(false);
                        grandfather.setColor(true);
                        current = grandfather;
                        continue;
                    } else {
                        if (current == parent.getLeftChild()) {
                            //TODO 情况2：当前节点的父节点是红色，叔叔节点是黑色，且当前节点是父节点的左子节点
                            rightRotate(parent);//父节点围着当前节点右旋
                            //右旋后，父节点与当前节点互换
                            Node temp = parent;
                            parent = current;
                            current = temp;
                        }
                        //TODO 情况3：当前节点的父节点是红色，叔叔是黑色，且当前节点是父节点的右子节点
                        parent.setColor(false);
                        grandfather.setColor(true);
                        leftRotate(grandfather);
                    }
                }
            }
        }
    }

    /**
     * 左旋
     *
     * @param x
     */
    private void leftRotate(Node x) {
        //TODO 第一步：把y的左子节点赋给x的右子节点
        Node y = x.getRightChild();
        x.setRightChild(y.getLeftChild());
        if (y.getLeftChild() != null) {
            y.getLeftChild().setParent(x);//y的左子节点的父节点变成x
        }
        //TODO 第二步：把y的父节点变成x的父节点
        y.setParent(x.getParent());
        if (x.getParent() == null) {//x是根节点
            root = y;
        } else {
            if (x == x.getParent().getLeftChild()) {//x是父节点的左子节点
                x.getParent().setLeftChild(y);
            } else {
                x.getParent().setRightChild(y);
            }
        }
        //TODO 第三步：把y的左在节点变成x
        y.setLeftChild(x);
        x.setParent(y);//x的父节点变成y
    }

    //右旋
    private void rightRotate(Node x) {
        Node y = x.getRightChild();
        //TODO 第一步：把y的右子节点赋给x的左子节点
        x.setLeftChild(y.getRightChild());
        if (y.getRightChild() != null) {
            y.getRightChild().setParent(x);//y右子节点的父节点变成x
        }
        //TODO 第二步：把y的父节点变成x的父节点
        y.setParent(x.getParent());
        if (x.getParent() == null) {//x是根节点
            root = y;
        } else {
            if (x == x.getParent().getLeftChild()) {//x是父节点的左子节点
                x.getParent().setLeftChild(y);
            } else {
                x.getParent().setRightChild(y);
            }
        }
        //TODO 第三步：把y的右子节点变成x
        y.setRightChild(x);
        x.setParent(y);//x的父节点变成为y
    }
}

 5、红黑树的查找操作

    5.1、基于二分查找

6、红黑树新增

    6.1、4中情况

    6.2、整体口诀

    6.2.1、情况1

如果新增节点为黑色，就会破坏黑色完美平衡，所以所有情况，新增的节点颜色都是红色

    6.2.3、情况3

GPU变色后，将G点变为新C点(将祖父节点作为新增节点C)

    6.2.4、情况4---CPG三点一线

G点旋转，GP变色

    6.2.5、情况4---CPG三角关系

将CPG三角关系转化为“三点一线”关系

红黑树在线测试演示：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

7、二叉树的平衡因子BF

BF：Balance Factor

定义：二叉树上节点的左子树高度  减去  右子树高度的值

BF的绝对值越大，说明这个树越不平衡

平衡因子是衡量二叉树的平衡性。

二叉树在线测试演示：https://www.cs.usfca.edu/~galles/visualization/BST.html

8、AVL树

AVL树在线测试演示：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

    8.1、定义性质

定义：平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树

性质：是一棵空树或任何一个节点BF绝对值不超过1

AVL树是完美平衡的树，对查找非常的友好。使用二分查找。

    8.2、自平衡

二叉树所有的自旋都是：父母围着子女转

    8.2.1、第一步

沿当前新增节点的父节点方向，查找最近失衡节点（最近的BF>1节点）

    8.2.2、第二步

以【最近失衡节点】为旋转节点进行一次或二次自旋

              圆心：就是新增节点那个方向的子节点（比如下图中的0008就是圆心）

方式1：一次自旋

方式2：两次自旋

如果“方式1---一次自旋”达不到平衡，就需要进行两次自旋

两次自旋：第一次（按照一次自旋的方式，找到圆心，将圆心作为选择旋转节点），【如下图：0777围着0800旋转】

                  第二次（第一次旋转完后，再将最近失衡节点作为旋转节点）【如下图：0888围着0800旋转】

    8.2.3、第三步

沿【最近失衡节点】的父节点向上游递归执行第一步、第二步操作