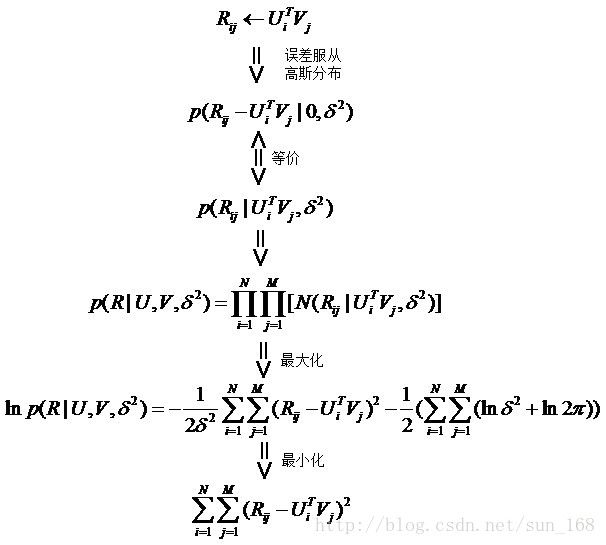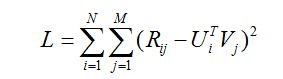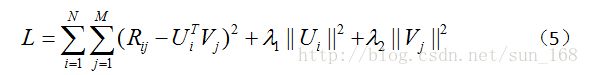自己动手写一个推荐系统
废话:
最近朋友在学习推荐系统相关,说是实现完整的推荐系统,于是我们三不之一会有一些讨论和推导,想想索性整理出来。
在文中主要以工程中做推荐系统的流程着手,穿插一些经验之谈,并对于推荐系统的算法的学术界最新的研究进展和流派作一些介绍。当然由于我做推荐系统之时还年幼,可能有很多偏颇甚至错误的见解,就当抛砖引玉,还请各位大大指点。
Reading lists
虽然很多人觉得作为AI的分支之一,推荐跟自然语言处理等问题的难度不可同日而语。但所谓磨刀不误砍柴工,我觉得,至少在开工前先应该阅读这样基本书,起码要看看目录,以对于推荐系统有个初步的了解。
中文书籍:
1.《推荐系统实践》项亮http://book.douban.com/subject/10769749/
这本书你说他好吧,不如recommend handbook;你说他不好吧,确实又把很多基础而简单的问题讲的很详细,而且还是中文的。薄薄的一本书,分分钟可以翻完,总而言之,是一本入门的好书。
外文书籍:
1.《Recommender Systems Handbook》Paul B. Kantor http://book.douban.com/subject/3695850/
其实所有敢自称handbook的书都是神书。这本书写的非常细,而且非常全,如果你去看一些推荐系统的一些比较冷门的topic的paper,比如fighting spam的,甚至能发现很多paper就是直接引用这本书里相关章节的内容。可以说这本书是做推荐同学必备的枕边书,没看过这本书出去吹牛逼时你都不好意思说自己是做推荐的,不过说实在,真正看完的没几个,一般是用到哪里查哪里,我刚才就去豆瓣验证了,几个做推荐的都是在读,一群文艺青年都是想读。此书唯一的缺点是没有出新版,有些地方已经成为时代的眼泪了。
2.《Recommender Systems - An Introduction》 Dietmar Jannach
http://book.douban.com/subject/5410320/
跟上面一本差不多,学院派的综述型的书,厚厚一本,不看的时候当枕头用。
3.《mahout in action》Sean Owen http://book.douban.com/subject/4893547/
上面的一中一外的书都是理论基础的书,这本书就和工程有些沾边。如果你要用mahout框架来做推荐系统,那么是必须要扫一遍的;如果你不用mahout,看看其中的流程和代码组织也是有一定好处的。
Paper:
由于《Recommender Systems Handbook》很多地方已经成为了时代的眼泪,这里推荐一些综述,以便开阔眼界。
一篇是physics report上面的recommend system这篇综述,可以说是最新最全的综述了,看完后学术界都在折腾啥分分钟就清楚了。http://arxiv.org/pdf/1202.1112v1.pdf
比较经典的是recommend system的state of art这篇综述,很多老一辈的同志喜欢推荐的,说实在这篇因为年代久远,也已经成为时代的眼泪了。
开工:
上面给了一些reading lists,并不是说要读完所有的才能开工,只是说,先看完个目录,哪里不懂查哪里。在下面介绍的做推荐系统的流程中,我只是想给大家介绍个普通的推荐系统该怎么做,所以很多地方都有偷懒,还请大家见谅。而且由于我不是做的在线的推荐系统,而是属于隔天推荐的那种离线的,所以叙述工程的时候就是只叙述离线的推荐。
数据准备:
一般来说,做推荐系统的数据一般分两种,一种从在线的读取,比如用户产生一个行为,推荐系统就反应下(传说豆瓣fm就是这么做的?),还有一种就是从数据库里读。
我个人一般是这样做的:跟做反作弊的人打个招呼,让他们在记用户行为数据的时候顺便存到各个线上服务器上,再写个php脚本,从各个服务器上把我需要的日志抓过来,然后当日要的最新的数据就来了。
但是这种地方其实存储的数据是加了一些判断的,也就是说是分类记录的(因为很多记录是别人刷的,比如丢一个链接到qq群里让别人帮忙投票什么的),这里不细说,到后面fighting spam的地方再讨论。
数据过滤:
当我们得到了每天产生的数据后,说实在这些数据实在是太多了,我们当然用不到这么多,就要写个过滤模块,把一些我们用不到的数据过滤掉。
我一般是这样做的:写个python的脚本,把过滤器放到一个单独的模块,要用的过滤器就到责任链里面注册下。这样别人和自己维护起来也方便点,顺便一说,过滤的东西一般来说有这样几种:一种是一个item只有一个user打过分的,而且以前没有人打分的,这样的数据放到推荐的模型里去跑虽然mahout会自动无视它,但其实按照power law来说是有不少的,内存能省就省吧;还有一种是有些黑名单的,有item和user各自的黑名单,这些也是事先要去掉的。
数据存储:
这个就是大家仁者见仁,智者见智的时候了,因为一般来说,是你选用的算法和算法具体的实现方式以及基础架构决定了你的存储方式,就不多说了。
我一般是这样做的:一般做成增量处理的方式,然后每天一计算,一周一回滚。由于算法实现的特殊性,每40个item user对存储在一起,有点类似于bitmap吧。
推荐系统算法部分:
这部分以前写过类似的小记录和心得笔记之类的东西,就直接贴了_(:з」∠)_
这里的推荐系统的核心算法主要用mahout实现。
各种算法对于推荐都有着自己的特定的假设,对于什么时候什么样的算法会有比较好的performance应该对于假设反复验证。说白了就是做实验。
然后我们一般用什么算法呢,看看mahout给的算法吧,花样繁多,什么item based,user based,slop-one,SVD等等,常用的都有了,那我们要用什么算法呢。
先简单说下user based的算法在mahout中的一些实现:
第一步应该先算出所有人的相似度矩阵W,再去对于item进行遍历,事实上mahout也是这样做的。
相似度矩阵也许可以保留下来,这样可以用来做谱聚类来验证。
UserSimilarity 封装了用户之间的相似性
UserSimilarity similarity = new PearsonCorrelationSimilarity (model);
UserNeighborhood封装了最相似的用户组
UserNeighborhood neighborhood = new NearestNUserNeighborhood (2, similarity, model);
总而言之,用DataModel来生成data model,用UserSimilarity生成User-user之间的相似度矩阵,用户的邻居的定义用UserNeighborhood定义,推荐引擎使用Recommender实现。
对于推荐的评判是使用evaluator来进行评判
double score = evaluator.evaluate(recommenderBuilder, null, model, 0.95, 0.05);
用95%的数据构建模型,用5%的数据进行test
Fixed-size neighborhoods
对于到底用多少人作为用户周围的一圈,我们事实上没有一个确定的值,就像做生物实验一样需要不断在特定的数据集里跑出来。
Threshold-based neighborhood
当然,我们也可以定义个threshold去找出最相似的用户群。
Threshold定义为-1到1(相似度矩阵返回的相似度就是在这个范围)
new ThresholdUserNeighborhood(0.7, similarity, model)
我们对于各个算法做个简单的比(吐)较(槽):
(假设我们是要像亚马逊一样对商品做推荐,然后我们最终是要做top k的推荐)
Item based
一般来说item-based要跑得快一些,因为item比user少
Slop one
说实在话我觉得在对于一些个人品味比较看重的东西上这个算法不是很靠谱
但是它在GroupLens 10 million数据的结果是0.65
当然,对于股票系统这种还是可取的
这个算法的假设是对于不同item的preference有种线性关系
不过slope-one有个好处是它的online算的很快,并且它的性能不由用户的数量决定
在mahout中的调用方法是new SlopeOneRecommender(model)
这个方法提供了两种weight:weighting based on count and on standard deviation
count 是越多的user的给越多的权重,对出的是一个加权的平均数
standard deviation则是越低的deviation给予越高的权重
这两个weight是默认采用的,当然disable它们只会让结果变得稍微坏一点0.67
不过这个算法有个很明显的缺点是比较占内存
但是幸运的是我们可以把它存在数据库里:MySQLJDBCDataModel
Singular value decomposition–based recommenders
事实上,尽管SVD失去了一些信息,但是有时候它可以改善推荐的结果。
这个过程在有用的方式平滑了输入
new SVDRecommender(model, new ALSWRFactorizer(model, 10, 0.05, 10))
第一个参数10是我们的目标属性个数
第二个属性是lambda->regularization
最后一个参数是training step跑的次数
KnnItemBasedRecommender
囧,事实上这个是用的knn的方式来做的算法,和前面的选择一个threshold然后圈画用户的算法是比较像的
但是用knn代价是非常高的,因为它要去比较所有的items的对
ItemSimilarity similarity = new LogLikelihoodSimilarity(model);
Optimizer optimizer = new NonNegativeQuadraticOptimizer();
return new KnnItemBasedRecommender(model, similarity, optimizer, 10);
结果也还不算差,是0.76
Cluster-based recommendation
基于聚类的推荐可以说是基于用户的推荐的算法的变体中最好的一种思路
对于每一个聚类里面的用户进行推荐
这个算法在推荐里面是非常快的,因为什么都事先算好了。
这个算法对于冷启动还是挺不错的
感觉mahout里面用的聚类算法应该类似于Kmeans?
TreeClusteringRecommender
UserSimilarity similarity = new LogLikelihoodSimilarity(model);
ClusterSimilarity clusterSimilarity =
new FarthestNeighborClusterSimilarity(similarity);
return new TreeClusteringRecommender(model, clusterSimilarity, 10);
注意的是两个cluster之间的相似度是用ClusterSimilarity来定义的
其中cluster之间的相似度还有NearestNeighborClusterSimilarity可选
吐槽:
对于算法的选择,其实我们是要和我们要推荐的目标挂钩的。为什么最近学术界搞SVD那一系的算法这么火,什么LDA,plsa各种算法层出不穷,事实上因为netflix的要求是要优化RMSE,在机器学习的角度来看,类似于回归问题,而工业界的角度来说,我们一般的需求是做top k的推荐,更加类似于分类问题。所以为什么相比用SVD系列的算法,用item based这种更加ad hoc的算法要表现的更好一些。当然2012年的KDD cup第一名的组用的是item based+SVD的算法,这是后话。
那么我就假设解我们这个top k的商品推荐的问题就用item based好了(速度快,结果又不算差),接下来就是确定相似度了。
相似度确定:
我们对于各个相似度做一些比(吐)较(槽):
PearsonCorrelationSimilarity
Pearson correlation:
coeff = corr(X , Y);
function coeff = myPearson(X , Y)
% 本函数实现了皮尔逊相关系数的计算操作
%
% 输入:
% X:输入的数值序列
% Y:输入的数值序列
%
% 输出:
% coeff:两个输入数值序列X,Y的相关系数
%
if length(X) ~= length(Y)
error('两个数值数列的维数不相等');
return;
end
fenzi = sum(X .* Y) - (sum(X) * sum(Y)) / length(X);
fenmu = sqrt((sum(X .^2) - sum(X)^2 / length(X)) * (sum(Y .^2) - sum(Y)^2 / length(X)));
coeff = fenzi / fenmu;
end %函数myPearson结束
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)、两个变量之间是线性关系,都是连续数据。
(2)、两个变量的总体是正态分布,或接近正态的单峰分布。
(3)、两个变量的观测值是成对的,每对观测值之间相互独立。
1.没有考虑到用户偏好重合的items的数量
2,只有一个item是相交错的话是不能得到correlation的,对于比较稀疏或者小的数据集这是个要注意的问题。不过一般来说两个用户之间只有一个item重叠从直觉上来说也不那么相似
Pearson correlation一般出现在早期的推荐的论文和推荐的书里,不过并不总是好的。
在mahout中使用了一个增加的参数Weighting.WEIGHTED,适当使用可以改善推荐结果
EuclideanDistanceSimilarity
Return 1 / (1 + d)
CosineMeasureSimilarity
当two series of input values each have a mean of 0(centered)时和PearsonCorrelation是有相同结果的
所以在mahout中我们只要简单的使用PearsonCorrelationSimilarity就好
Spearman correlation
这个方法用rank的方式,虽然失去了具体的打分信息,不过却保留了item的order
Return的结果是-1和1两个值,不过和pearson一样,对于只有一个item重叠的也算不出。
而且这个算法比较慢,因为它要算和存储rank的信息。所以paper多而实际用的少,对于小数据集才值得考虑
CachingUserSimilarity
UserSimilarity similarity = new CachingUserSimilarity(
new SpearmanCorrelationSimilarity(model), model);
Ignoring preference values in similarity with the Tanimoto coefficient
TanimotoCoefficientSimilarity
如果一开始就有preference value,当数据中signal比noise多的时候可以用这个方法。
不过一般来说有preference信息的结果要好。
log-likelihood
Log-likelihood try to access how unlikely 这些重叠的部分是巧合
结果的值可以解释为他们的重合部分并不是巧合的概念
算法的结果可能比tanimoto要好,是一个更加聪明的metric
Inferring preferences
对于数据量比较小的数据,pearson很难handle,比如一个user只express一个preference
于是要估计相似度么.........
AveragingPreferenceInferrer
setPreferenceInferrer().
不过这种办法在实际中并不是有用的,只是在很早的paper中mention到
通过现在的信息来估计并不能增加什么东西,并且很大的降低了计算速度
最终我们要通过实验来比较上面的相似度,一般来说是用准确率,召回率,覆盖率评测。
这里有一篇Building Industrial-scale Real-world Recommender Systems
http://vdisk.weibo.com/s/rMSj-
写netflex的,非常好,我就不献丑多说了,所以上面只是吐槽下常见的算法和相似度。
其实算法按流派分是分为下面这些类别的,大家有兴趣也可以了解下,我这里就不多做介绍:
Similarity-based methods
Dimensionality Reduction Techniques
Dimensionality-based methods
Diffusion-based methods
Social fltering
Meta approaches
我上面所说的相似度和推荐算法,只能算是Similarity-based methods和Dimensionality Reduction Techniques里的非常小的一小部分,只当抛砖引玉了。
Ps:刚在豆瓣上问了下,他们说就用前两种,事实上我也是觉得协同过滤+SVD 偶尔做做topic model就够了 如果没事干再上点social trusted的东西
增加规则:
记得hulu在做presentation的时候说过“不能做规则定制的推荐系统不是一个好的推荐系统”(好像是这样吧......)事实上我们做出来的推荐的结果是需要做很多处理再展现给用户的,这时候就是需要增加规则的时候了。
1.改善推荐效果:有些协同过滤的算法,做出来的结果不可避免的产生一些让人啼笑皆非的结果,比如用户什么都买,导致你有可能跟姑娘们推荐的时候在佛祖下面推荐泳装什么的(真实的故事)。这时候就有两种办法,一种就是调整模型,一种就是增加规则做一定的限制。再举个常见的例子就是有时候会在推荐冬装的时候出现夏装什么的,这时候一般我的处理方式是给这种季节性商品做一个随时间的衰退。
2.增加广告和导向:插入广告,我们的最爱,这个就不多说了,靠规则。而所谓用户喜欢的,其实不一定就是最好的,比如用户一般来说就喜欢便宜的,还有什么韩流爆款之流,如果你推出来的东西都是这样的,整个系统就变成洗剪吹大集合了,非常影响定位,这时候也要上规则。
3.做一些数据挖掘和fighting spam的工作:这个在fighting spam的地方细说
可视化参数调整:
做完上面的工作,一般来说推荐系统的基础架构就差不多了,但是往往各个算法以及你自己上的规则都有多如牛毛的参数要调整,这时候一般要自己写个测试脚本,将调整的结果可视化下一下,我个人推荐的是highchart,看参数以及比较各个指标非常清爽, 还可以自己做一些比如是取log之类的定制,很是方便。http://www.highcharts.com/
调整参数以及上线:
上线前有两个事要做,一般来说就是离线测试和AB test。
离线测试就是把数据抽样一部分,分为train data和test data,然后评估一些准确率,召回率以及coverage之类的指标,用上面的可视化工具观测比较下,感觉差不多了把pm叫过来让她给小编们看看,看看审美和效果之类的。这是比较粗糙的,有的地方做的比较过细,还有用户调研和请一些人来实际使用,这是后话。
AB test也是大家最喜欢的地方了。因为说实在,评估推荐系统学术界是看准确率那一些东西,但是工业界还是看pv uv转化率这种实打实带来效益的东西,而AB test就是评估这些的。我个人是比较推荐这种方法,说不上好,只是抛砖引玉,就是按一般的做法先空跑一个星期,然后再把系统上线实际做算法pk,然后选取的实验用户一半的几率进入原来的算法的推荐,一半的几率进入你的算法的推荐,每天看看转化率之间的比较,顺便还可以调下参数做做实验。如果算法稳定表现较好,就差不多了。
Fighting spam:
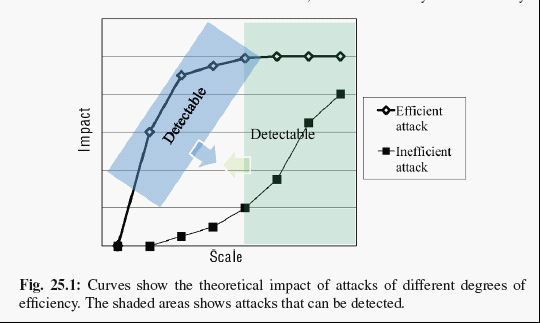
俗话说,有人的地方就有江湖,有推荐的地方就有人刷。刷子一般分三种类型的:average random和nuke。一般来说,average和random比较好对付,只要你的系统鲁棒性好点,基本影响不大。但是nuke的就非常烦,一般来说有两种思路解决,一种是提高系统鲁棒性,另外就是上规则。我们从这张图看看两种思路分布对应的解决效果:
其实鲁棒性的系统做的就是把efficient attack的曲线降低,其实效果不算太好。
规则就是做到提前检测,将危险扼杀在摇篮之中,就是做的蓝色的那块detectable的部分。
Fighting spam是个博大精深的问题,俗话说,与人斗,其乐无穷,就是说的这个意思。
我们从规则说来,一般来说规则可以放到最前面的数据收集和过滤的阶段,比如在收集数据的时候看看这个人是否是多个账号但是是一个ip,或者有些人用户名或者注册邮箱有群体相似性质,或者有没有出现pv等不正常的情况。有时候我们也可以从推荐的结果里上规则来查,比如有些人刷的过火了,导致推荐结果出现一些问题,我们就可以用迭代的方式按照先验的刷子的比例来排出刷子排行榜之类的东西。这些都是经验之谈,上不了台面,大家也可以自己摸索。
结束:
上面啰嗦了半天,大体上做一个完整的简单推荐系统就是涉及到上面这些步骤。一些地方说的不够详细,有些是因为我懒,有些是不方便说。大家觉得我说的不对或者不妥的地方,可以直接在下面跟帖喷,或者有大大指导我也是很欢迎的,大家多交流经验。我的邮箱是[email protected] 豆瓣是http://www.douban.com/people/45119625/ 有什么问题也可以豆瓣或者邮件交流。
其实我是觉得,要是有个大大说“你个傻缺,写的狗屁不通,让我来教你我是怎么做推荐的”就更好了。
推荐系统小结
推荐系统(RecSys)作为电子商务中一个很火的应用,主要是为了帮助用户发现可能感兴趣的东西,这种就叫做个性化推荐系统;而广告商还可以利用结果将内容投放给可能会对它们感兴趣的用户,这就成了个性化广告。比较著名的推荐系统有亚马逊,被RWW(读写网)称为“推荐系统之王”,你从亚马逊买了一本书以后,会发现它会经常向你的邮箱发一些相关的书籍,这个有时比较恼人,呵呵;此外还要电影和视频网站,像YouTube和Hulu等会美国比较著名的视频网站;个性化音乐网络电台,像国际的Pandora和Last.fm以及国内的豆瓣电台;社交网络,如Facebook等;个性化阅读,如GoogleReader等;个性化邮件和个性化广告等。
架构
主流的推荐系统的架构如下图:
而动态推荐系统的架构如下:
关于推荐系统的架构,这几篇文章写得不错,这里mark一下。
推荐系统的架构,
http://www.cnblogs.com/kobedeshow/p/3569525.html?utm_source=tuicool
淘宝推荐系统,
http://www.biaodianfu.com/taobao-recommendation-system.html?utm_source=tuicool
InfoQ上关于Hulu的视频推荐系统架构经验,
Hulu推荐系统构建经验谈,
http://www.infoq.com/cn/presentations/hulu-recommendation-system-construction-experiences/
算法
推荐系统的实现算法,按照使用的数据,主要分为以下三种算法:
− 协同过滤:用户的行为数据,像点击、评分、购买等;
− 内容过滤:用户内容属性和物品内容属性;
− 社会化过滤:用户之间的社交网络关系,如朋友、关注关系等。
按照模型划分,主要有以下三种:
− 最近邻模型:基于用户/物品的协同过滤算法;
− Latent Factor Model:基于矩阵分解的模型;
− 图模型:二分图模型,社会网络图模型等。
除了推荐系统自身的问题,像冷启动、数据的稀疏性问题等,还有一个需要关注的问题,就是推荐系统的时间效应问题,比较常见的时间效应问题主要反映在用户兴趣的变化、物品流行度的变化以及商品的季节效应。即下面主要考虑三个问题,如何建立动态用户兴趣模型,如何建立用户长期兴趣和短期兴趣的动态用户兴趣模型,还有网站时效性对用户行为和推荐系统设计的影响。
考虑到推荐系统的时间效应问题,可以将协同过滤所使用的数据集归结为一个四元组,即{用户,物品,行为,时间},那么现在就面临一个问题,如何通过研究用户的历史行为和兴趣爱好,预测用户将来的行为和喜好。需要解决以下三个问题:动态评分预测、动态Top-N推荐、时效性的影响。
对于第一个问题,动态评分预测问题。数据集可以选用比较直观的显性反馈数据集,即(用户,物品,评分,时间),研究是这样一个问题,给定用户u,物品i,时间t,预测用户u在时间t对物品i的评分r。对于该类问题,相关的算法已经有了很多的研究,与时间无关的评分预测问题算法主要有以下几种:
− 基于用户/物品的协同过滤算法;
− 基于矩阵分解的模型LatentFactor Model;
− 受限波尔兹曼机RBM。
与时间相关的评分预测问题算法主要是基于下面两种想法:
− 用户会喜欢和他们最近喜欢的物品相似的物品;
− 用户会喜欢和他们兴趣相似的用户最近喜欢的物品。
当然上面的这些算法是提出来了,但是有些地方有待优化。
上述算法需要考虑的时间效应问题主要有以下几个方面:
用户兴趣的变化,比如说:年龄增长,从青年长成中年壮年;生活状态的变化,由以前的学生到踏上工作岗位;社会热点问题的影响,奥运会等。此外还有季节效应问题,一些在夏季很流行的,在秋冬季节未必就很流行。如何解决上述问题,提出优化还有待进一步思考。
对于动态Top-N推荐问题,数据集选用的是不太直观的隐性反馈数据集,{(用户,物品,时间)},研究的是这样的一个问题,给定用户u,时间t,预测用户u在时间t可能会喜欢的物品列表R(u)。在这方面的相关研究也很成熟,有基于邻域的协同过滤算法,主要分为两种,一种是ItemCF,推荐给用户那些跟他们之前喜欢的物品类似的物品;还有一种是UserCF,推荐给用户那些跟他们兴趣相似的用户喜欢的物品。还有基于评分数据的Top-N推荐算法,该想法的思路是推荐给用户那些他们可能评分最高的物品。该想法都是围绕用户的兴趣展开的,需要考虑到,用户兴趣分为短期兴趣和长期兴趣,短期兴趣的特点是临时、易变;长期兴趣的特点是长久、稳定;用户的短期兴趣可能会转化为长期兴趣,所以需要在推荐时综合考虑长期兴趣和短期兴趣。该问题的解决有待进一步思考。
对于时效性的影响,每个在线系统都是一个动态系统,但它们有不同的演化速率。比如说,新闻,博客演化的很快,但音乐,电影的系统演化的却比较慢。这就带来这样一个问题,不同演化速率的系统需要不同类型的推荐算法,如何解决该问题,也是应该进一步深入思考的。
最近一直学习Mahout和推荐引擎相关的知识,一直想搞清楚,什么样的推荐系统的架构才是合理,既能对海量数据进行复杂运算,又能及时响应做出推荐。在网上发现一篇对推荐系统结构讲解的很好的文章数:据驱动销售——个性化推荐引擎,里面提到这样的思想“ 数据的特性对我们的架构设计起到了一个非常关键的作用,因为我们可以使用完全不同的方式来将静态数据和动态数据分开处理,再合并分析 ”,对于一个数据挖掘初学者的我,很受启发。
同时,自己也在思考,若结合实际的推荐系统中,针对不同的协同过滤算法,如何来划分动态、静态数据,它们是怎样的结构,怎么存储的,又是怎么合并分析的。根据文章作者对推荐系统的设计思路,结合Mahout的源码实现,我似乎找到了一些相似之处,来解释上面的问题。
首先,仔细缕一遍Mahout产生推荐的算法流程:
1. 原始数据,Mahout中所有协同过滤算的的输入数据,都要求这样的结构(UserID、ItemID、Preference)为一条记录,表示一个用户对某一个商品的喜爱程度;怎么得出这样的结果,Mahout并没实现,值需要你输入;一般来讲是通过分析用户各类行为日志记录,结合一些特征属性,计算出来。
2. 根据不同的协同过滤算法,得到用户与用户的关系(基于用户的) 或 商品与商品的关系(基于商品的);这时的数据结构,更像是矩阵:UserAID(ItemAID)、UserBID(ItemBID)、Value(相似度)。
3. 计算推荐列表,这一步比较细碎,根据不同的推荐算法,会有些许不同,但大体流程是不变;首先会计算出可能被推荐的书籍(基于用户的协同过滤算法,会先找出此用户的邻居,依次找出这些邻居喜欢的商品且此用户未浏览的商品;而基于商品的协同过滤算法,则直接找出所有此用户未浏览的商品);其次逐个计算这些可能被推荐的商品的得分,并以此得分由高到底的排序;最后返回前面N个(N可有客户端作为请求参数而指定)。
都知道,Mahout框架式基于Hadoop的,这样分布式的运算以便海量数据的处理;然而Mahout的实现却又很多种(哪怕是同一个算法),也许Mahout是为了给开发者提供多种实现的选择;我自己总结了一下,它的实现模式根据Hadoop框架的使用情况大概可分为三种:
第一种:完全不使用Hadoop,上述的逻辑均在单机里完成,为了达到效率,在第二步时,Mahout提供一个参数maxEntries来控制总数据量。
第二种:部分使用Hadoop,即在上述逻辑中第二步运算用户与用户关系或商品与商品关系时使用Hadoop,将运算结果持久化;后续的计算由单机完成后并展示。
第三种;完全是Hadoop运算,运算完以后的结果为:每个用户有一个推荐列表;展示的话直接查库就OK
根据那片文章中作者描述的推荐系统结构,采用第二种实现是相对合理的,因为关系数据相对静态,并且此部分的数据量是十分庞大,它类似矩阵,若你用户数量或商品数量而M,那它的数据量为M*(M-1)/2,若全部放在内存中,会占用大量的资源,对静态数据来讲完全没有必要。
而在第三步为用户计算推荐列表时,又可以结合用户的一些在线属性或浏览情况得到一些实时变化的推荐产生更好的用户体验。
推荐系统:总体介绍、推荐算法、性能比较
探索推荐引擎内部的秘密,第 1 部分: 推荐引擎初探
个性化推荐技术漫谈
一些推荐算法:
SVD: SVD在推荐系统中的应用
slope one:推荐系统:Slope One 算法
apriori:先验算法
推荐系统:关联规则(2)
FP-Growth:推荐系统:关联规则(3) —— FP-Growth 算法
Item CF :推荐系统:协同过滤 之 Item-based Collaborative Filtering
User CF:推荐系统:协同过滤 之 User-based Collaborative Filtering
算法间比较:
推荐系统的常见推荐算法的性能比较
相似性计算:
探索推荐引擎内部的秘密,第 2 部分: 深入推荐引擎相关算法 - 协同过滤
由于需要准备一月底与三月中两个关于“推荐系统”的短期课程(前者在阿卜杜拉国王科技大学,没错就是那个传说中沙特的土豪大学!后者在悉尼科技大学),期间二月份还夹带了一个推荐系统相关的讨论班,所以从去年十二月开始我几乎每个周末至少得抽出一天的时间来做幻灯片。推荐技术是我个人研究兴趣并不是我日常工作内容,无法利用上班时间准备,再加上我有强迫症(必须要让累加起来多达二百多页的幻灯片风格色调字体公式图例都保持视觉上的审美愉悦与逻辑上的高度统一),所以在画图敲公式上花了很长时间。幻灯片做烦了,突然很想写点东西聊聊我对推荐系统的见解。此文不会出现公式,尽量用白话说清楚目前主流推荐技术的直观原理。
先谈谈问题背景,故事是这样的:互联网出现后,随着网上内容的增加,好学的小伙伴们发现很多他们不懂的姿势网上都有,可互联网不像图书馆搞个书目索引就行,于是出现了搜索引擎帮助小伙伴们在茫茫互联网上找到他们感兴趣的东西,但条件是你必须知道你想要什么,然后提取成关键字去搜,所谓信息检索(Information Retrieval)。十年过去了,信息爆炸了,问题出现了,搜索引擎动辄返回几十万个结果,或者有些想要的信息却根本不知道它的存在,甚至根本不知道如何用关键词描述你想要的东西,这时推荐系统应运而生——小伙伴们不用自己去找,推荐系统就会根据小伙伴们的个人资料历史纪录从海量信息中自动筛选符合小伙伴们口味的内容进行推荐,所谓推荐系统(Recommender Systems)。如今,推荐系统已经无处不在,几乎所有的网络服务都集成了推荐系统。在此我就不提那些学术圈老掉牙的例子什么Netflix电影推荐啊Google新闻推荐啊Yahoo!广告推荐啊什么的了;我瞄了下自己的手机举几个例子吧:微博朋友推荐、虾米音乐推荐、LinkedIn工作推荐、YouTube视频推荐、大众点评餐馆推荐、等等。
既然要谈的是推荐“技术”,那么我得先把推荐问题用数学语言形式化了。淡定淡定,推荐问题形式化后非常简单干净——就三个矩阵(从这里往下得有一丢丢想像力,能在脑海里想象简单的矩阵操作)。最重要的一个矩阵是评分或偏好矩阵(Rating/Preference Matrix),其每一行对应一个用户,每一列对应一件物品,矩阵中的任一元素就是某用户对某物品的感兴趣程度(评分可以用正整数表示,点赞神马的可以用0/1表示),不失一般性,下面我们仅基于评分矩阵讨论。这个评分矩阵是极其稀疏的,因为每个用户只可能对很少一部分物品打分。第二个矩阵是用户信息矩阵,每一行对应一个用户,每一列对应一个用户属性(如年龄、职业、地区、标签等)。第三个矩阵是物品信息矩阵,每一行对应一件物品,每一列对应一个物品属性(如电影的流派、导演、演员等)。推荐问题的目标就是:基于给定的三个矩阵,把评分矩阵中缺失元素的评分预测出来,并基于预测出来的评分把得分高的物品推荐给相应用户。这里值得注意的是,只有评分矩阵是所有推荐技术所必需的,用户信息矩阵与物品信息矩阵这两者是可选的。真实推荐系统面临最大的挑战是评分矩阵的大规模与稀疏性。
接下来我把一些当前常用的推荐技术分门别类。推荐技术可先分为三大类:基于人口统计的推荐技术(Demography-based)、基于物品内容的推荐技术(Content-based)、以及基于协同过滤的推荐技术(Collaborative Filtering,简称CF)。基于人口的又包括基于用户资料的(User Profile)和基于信任关系的(社交网络上的好友关系)等。基于物品内容的又可细分为基于元数据的(即Metadata,比如电影的流派、导演、演员等)和基于内容数据的(比如视频数据、音频数据)等——真实应用大多是基于元数据的,基于内容数据的推荐系统由于语义鸿沟(Semantic Gap)和效率问题,做了几十年,一直未突破(深度学习能突破么,拭目以待呵呵)。虽然基于人口和基于内容的两大类推荐技术在实际中的应用极广而且效果在某些应用场景下不比第三类技术协同过滤差,那为什么协同过滤技术一跃成为当今主流的推荐技术了呢?有以下几方面原因:1)协同过滤问题相当干净,只需要一个评分矩阵,不需要用户信息与物品信息,这解决了用户物品信息缺失场景下的推荐问题。2)协同过滤问题的本质是矩阵补全问题(Matrix Completion),也就是把一个稀疏矩阵的缺失元素给估计出来,这是机器学习中一个经典问题,除了推荐之外还有无数的应用都可归结为矩阵补全问题,所以机器学习的高速发展也促进了协同过滤技术。3)2006年Netflix发起的那个百万美元大奖功不可没,直接上演了持续多年相关研究领域全民做推荐的激情岁月,虽然吧这个竞赛使用了一个完全误导的评价指标来判断推荐算法的优劣(使用的是RMSE指标,这是一个评价回归的指标,而推荐问题事实上是一个排序问题)。跑题了,接着分类。协同过滤技术可以继续分为基于记忆的(Memory-based)和基于模型的(Model-based)。基于记忆的继续可分为基于用户的(User-based)和基于物品的(Item-based);而基于模型的可以继续分为基于矩阵分解的(Matrix Factorization)和基于联合聚类的(Co-clustering)。基于记忆的协同过滤技术使用的是K-近邻(K-Nearest Neighbors)的思想,而基于模型的协同过滤技术使用的是机器学习方法。分类结束。
真实系统都是使用的混合策略(Hybrid Strategy),多为基于人口、基于元数据、以及基于用户或物品的协同过滤推荐技术的各种组合。基于模型的协同过滤虽然使用了高端大气上档次的机器学习方法,但做过真实应用的同学都懂的,简单粗暴才是王道,提出并改进一个模型连发三篇顶级机器学习会议论文提高了一个百分点,往往不如真实系统中屌丝程序员在哪疙瘩加个莫名的阈值来得有效。那为什么顶尖互联网企业都在搞机器学习呢?这么说吧,五百的衣服和五万的衣服功能都是一样的,但是地位高到一定程度,除了衣服的基本功能外我们还会追求一些其它的东西。但是如果只是想基于推荐技术做一个网络服务神马的,就没必要搞那么玄的机器学习花样了,反而大规模计算的效率问题和推荐应用本身是否有市场前景是更应该考虑的,有了这些,最基本的基于人口统计与基于记忆的推荐技术就能搞定大多数应用。貌似跑题了,接着说混合策略。有些混合策略是对不同推荐技术的结果加权相加(Weighting);有些是根据场景不同在不同技术间跳转(Switching),比如新用户基于人口统计老用户基于协同过滤;有些是一个网页上不同区域同时显示不同推荐技术的结果(Mixing);有些是用一个推荐技术对另一个推荐技术输出的结果进行提升(Cascading)。
除了基于模型的协同过滤技术外,其它的推荐技术在原理上都相对简单,使用一些相关查询和启发式算法就能解决。这段就把除基于模型的协同过滤以外的推荐技术都简单介绍下。首先是基于人口统计学的,该类推荐技术需要基于用户信息矩阵和评分矩阵。原理很简单,就是查找用户信息矩阵中背景类似的用户,然后把对应评分矩阵中打高分的物品推荐给背景类似的用户。举个例子,用户信息上显示两个人年龄相仿居于湾区互联网从业者,于是系统就会认为这两人相关性强会有共同爱好,把其中一人打高分的电影推荐给另一个。这种推荐技术的优点是简单,一些相关性查询操作就能搞定,而且没有“冷启动(Cold-start)”问题(即用户缺失历史评分纪录);缺点是无法个性化推荐,基于人口统计相似度的假设太强,比如同为IT男,一个技术宅,一个伪文青,你把技术宅喜欢的东西推荐给伪文青肯定是不靠谱的,比如我排斥一切XX侠的电影。接下来是基于物品内容的推荐技术,该类推荐技术需要基于物品信息矩阵和评分矩阵(这里只讨论基于元数据的,基于真实内容的开门课都讲不完)。该类推荐技术的原理也很简单,基于元数据计算物品之间的相关性,然后把与该用户以前打高分的物品最相关的物品推荐给他。这类推荐技术比前一种靠谱,因为用户在同类物品上一般会表现出相同的兴趣程度。举个例子,我如果对《巴黎我爱你》打了个高分,那么推荐系统就会向我推荐强关联的《纽约我爱你》,而我也会对同一血统的电影很感兴趣。因此,该类技术的优点就是对偏好的建模较为精细与准确;缺点是依赖于物品元数据包含的信息量,以及存在冷启动问题(需要用户的历史评分)。接下来介绍基于记忆的协同过滤技术,该类推荐技术的标准问题设置仅需要评分矩阵,当然近年来学术界有些关于迁移学习(Transfer Learning)在推荐系统中的研究会使用到用户与物品的信息矩阵、甚至使用另一个域的评分矩阵(我以前在推荐系统中的工作主要在这块,感兴趣的同学可以用谷歌百度下一个二页纸的小文“Cross-Domain Collaborative Filtering: A Brief Survey”),但这里我们只讨论标准的协同过滤问题设置。基于用户的协同过滤分为两步:第一步是计算用户之间的相关度,这里的相关度是评分矩阵行向量间的相关度,其直观意义就是如果两个用户在相同物品上打的分越接近,那么这两个用户的偏好也越接近。如果评分矩阵是一个没有缺失项的满矩阵,那么行向量之间的相似度直接可以用欧式距离或者夹角余弦计算;由于评分矩阵是稀疏矩阵,因此计算相关性首先要把两个行向量之间的交集(打过分的物品)找出来,并只在该交集上计算一个类似夹角余弦的值,叫作皮尔森相关系数(Pearson Correlation Coefficients)。在取得了与所有用户两两之间的相关性后,第二步就是预测该用户的缺失评分。给定一个待预测用户,找到他的K-近邻用户集合,他的缺失评分就是用其K-近邻用户对应物品上的历史评分用相关性加权平均得到。基于物品的协同过滤和基于用户的是对称的,一个是对行操作,一个是对列操作,方法和原理都是一样的。
从这里往后的内容主要将介绍基于模型的协同过滤技术。在大多数推荐系统的介绍中一般直接就把基于模型与矩阵分解等同起来了,因为应用到实际推荐系统中的基于模型的推荐技术一般都是基于矩阵分解的,比如Netflix百万大奖得主提出的(Time)SVD++方法(但事实上前几名所用的方法都是很多种算法集成的结果,所以说研究归研究,在实际应用中干净优美的模型很难超越东拼西凑再加点人脑规则的四不像,这个道理我早在八年前做TRECvid的时候就总结出来了,当时直接导致我放弃多媒体研究直到现在一直对计算机视觉抱有悲观态度)。又跑题了,继续说基于模型的推荐技术。除了矩阵分解,这里我还要额外介绍一种基于联合聚类的技术,所谓联合聚类,就是对用户与物品(即评分矩阵的行与列)同时聚类,聚类的方法可以是简单的K-Means,但更优美的建模方法是双向混合模型——我个人非常喜欢这种建模方式,虽然对于评分预测的性能没有基于矩阵分解的好(因为矩阵分解的目标就是拟合评分而混合模型的目标是估计用户与物品在潜在类型上的分布)。
先说基于矩阵分解的方法吧。给定一个评分矩阵(大小为N*M),把该矩阵分解为两个矩阵的乘积,一个是用户特征矩阵(大小为N*K),一个是物品特征矩阵(大小为M*K),其中潜在特征(latent features)的维度远小于用户数与物品数;目标函数就是两个特征矩阵的重构与给定评分矩阵在那些可见评分上的值尽可能接近,一般使用矩阵范数(Frobenius norm),即两个矩阵相减所有元素上残差平方和;再加上对两个特征矩阵的矩阵范数作为正则化项。改优化问题常用两种方法解决:一种是交替最小二乘(Alternative Least Squares),交替优化用户特征矩阵与物品特征矩阵,在优化其一的时候固定另一个的值视其为已知,这样就相当于每轮解决一个标准的最小二乘问题,最后收敛到局部最优解。该方法的优点是收敛速度快,缺点是需要对用户数与物品数大小的方正求逆,难以规模化。另一种是随机梯度下降(Stochastic Gradient Descent),对每个用户与每个物品(评分矩阵的行与列)分别求偏导建立牛顿迭代公式,然后用可见评分顺序对这些迭代公式进行更新。该方法的优点是可以并行化、效率高,目前大规模矩阵分解都是用的这种优化算法;缺点可能是收敛速度没有第一种快(这点我不是很确定)。最后说说这种形式矩阵分解的物理含义。这样分解成两部分后,就相当于用户和物品都被放置到一个潜在的K维特征空间,只要拥有相似潜在特征的用户与物品,他们的夹角就小乘积就大得到的预测评分也就相应更高。那么凭什么我们能指定一个“潜在的K维特征空间”呢?拿Pandora的音乐推荐举例子,每个音乐有几百条“音乐基因”就是音乐的显式特征(不知道音乐基因的可以去古歌百度一下Music Gene Project)。如果不降维的话,那么音乐特征矩阵和用户特征矩阵的纬度就是其真实的特征纬度。假设我们基于主成分分析(PCA)用相同的一套基分别对这两个矩阵进行线性变换,那么得到的两个矩阵就可以认为是投影到潜在特征空间的两个矩阵,而这两个矩阵的乘积和原来的两个矩阵是一样的(因为当中两个投影矩阵的乘积是单位矩阵)。那么假如我们只用前K个基投影呢?那我们就得到了只有K维潜在特征空间的低秩矩阵。所以在实际问题中,我们都不需要知道真实的特征空间,只需要人为指定一个K维潜在特征空间就可以了,得出的结果可以认为是真实特征经过某个线性变化后投影到一个低维潜在特征空间。
最后介绍基于联合聚类的方法。这类方法的物理意义更直观,其实也能表示成为矩阵分解的形式,但不同的是联合聚类把评分矩阵(大小为N*M)分解为三部分,一个是用户隶属度矩阵(N*K),表示每个用户在K个潜在用户组上的分布情况,所有元素为正每行加起来为1;一个是物品隶属度矩阵(M*L),表示每个物品在L个潜在物品组上的分布情况,所有元素为正每行加起来为1;还有一个是压缩评分矩阵(K*L),表示某个用户组对某个物品组给的评分。使用这三个矩阵的乘积重构评分矩阵可以对缺失评分进行预测。解决该问题最简单的方法是分别对行与列进行K-Means聚类,然后用户与物品隶属度矩阵就根据聚类结果把对应的组设为1其它为0(硬聚类),而压缩评分矩阵是每个联合聚类中评分的平均值。更一般性的建模方法是令两个隶属度矩阵为在潜在组别上的分布(软聚类),这需要使用期望最大(Expectation-Maximization)算法解决;进一步地考虑贝叶斯,由于隶属度就是Dirichlet分布,那么其实该联合聚类问题可以使用Latent Dirichlet Allocation的变种建模,叫作Bi-LDA,使用吉布斯采样解决。这类方法的具体细节就不介绍了。
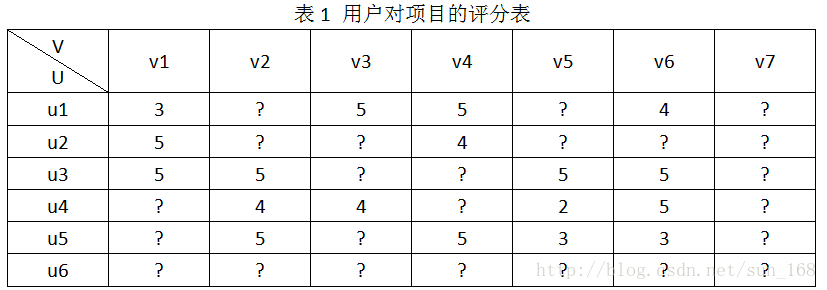
为了方便介绍,假设推荐系统中有用户集合有6个用户,即U={u1,u2,u3,u4,u5,u6},项目(物品)集合有7个项目,即V={v1,v2,v3,v4,v5,v6,v7},用户对项目的评分结合为R,用户对项目的评分范围是[0, 5]。R具体表示如下:
推荐系统的目标就是预测出符号“?”对应位置的分值。推荐系统基于这样一个假设:用户对项目的打分越高,表明用户越喜欢。因此,预测出用户对未评分项目的评分后,根据分值大小排序,把分值高的项目推荐给用户。怎么预测这些评分呢,方法大体上可以分为基于内容的推荐、协同过滤推荐和混合推荐三类,协同过滤算法进一步划分又可分为基于基于内存的推荐(memory-based)和基于模型的推荐(model-based),本文介绍的矩阵分解算法属于基于模型的推荐。
矩阵分解算法的数学理论基础是矩阵的行列变换。在《线性代数》中,我们知道矩阵A进行行变换相当于A左乘一个矩阵,矩阵A进行列变换等价于矩阵A右乘一个矩阵,因此矩阵A可以表示为A=PEQ=PQ(E是标准阵)。
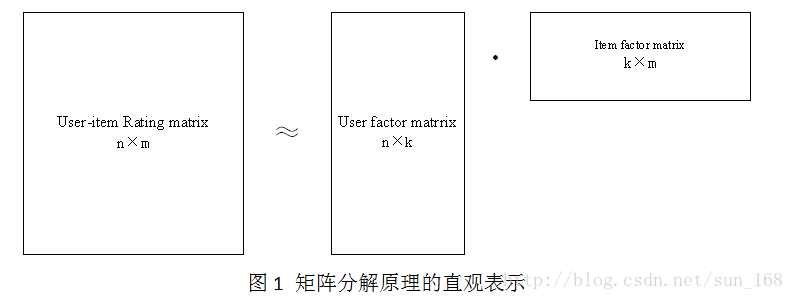
矩阵分解目标就是把用户-项目评分矩阵R分解成用户因子矩阵和项目因子矩阵乘的形式,即R=UV,这里R是n×m, n =6, m =7,U是n×k,V是k×m。直观地表示如下:
高维的用户-项目评分矩阵分解成为两个低维的用户因子矩阵和项目因子矩阵,因此矩阵分解和PCA不同,不是为了降维。用户i对项目j的评分r_ij =innerproduct(u_i, v_j),更一般的情况是r_ij =f(U_i, V_j),这里为了介绍方便就是用u_i和v_j内积的形式。下面介绍评估低维矩阵乘积拟合评分矩阵的方法。
首先假设,用户对项目的真实评分和预测评分之间的差服从高斯分布,基于这一假设,可推导出目标函数如下:
最后得到矩阵分解的目标函数如下:
从最终得到得目标函数可以直观地理解,预测的分值就是尽量逼近真实的已知评分值。有了目标函数之后,下面就开始谈优化方法了,通常的优化方法分为两种:交叉最小二乘法(alternative least squares)和随机梯度下降法(stochastic gradient descent)。
首先介绍交叉最小二乘法,之所以交叉最小二乘法能够应用到这个目标函数主要是因为L对U和V都是凸函数。首先分别对用户因子向量和项目因子向量求偏导,令偏导等于0求驻点,具体解法如下:
上面就是用户因子向量和项目因子向量的更新公式,迭代更新公式即可找到可接受的局部最优解。迭代终止的条件下面会讲到。
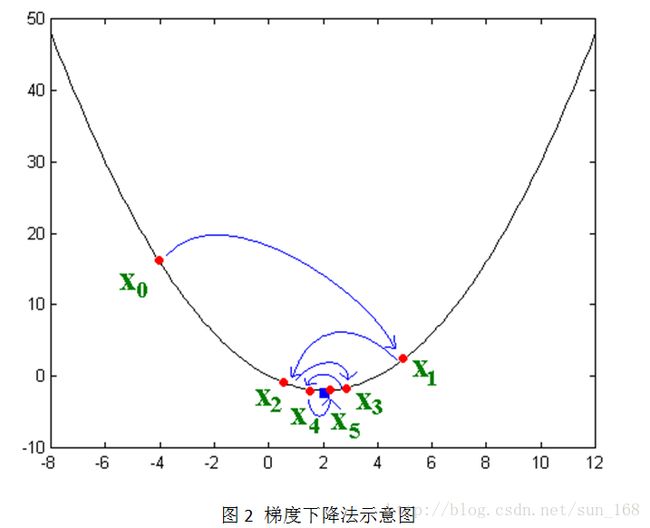
接下来讲解随机梯度下降法,这个方法应用的最多。大致思想是让变量沿着目标函数负梯度的方向移动,直到移动到极小值点。直观的表示如下:
其实负梯度的负方向,当函数是凸函数时是函数值减小的方向走;当函数是凹函数时是往函数值增大的方向移动。而矩阵分解的目标函数L是凸函数,因此,通过梯度下降法我们能够得到目标函数L的极小值(理想情况是最小值)。
言归正传,通过上面的讲解,我们可以获取梯度下降算法的因子矩阵更新公式,具体如下:
(3)和(4)中的γ指的是步长,也即是学习速率,它是一个超参数,需要调参确定。对于梯度见(1)和(2)。
下面说下迭代终止的条件。迭代终止的条件有很多种,就目前我了解的主要有
1) 设置一个阈值,当L函数值小于阈值时就停止迭代,不常用
2) 设置一个阈值,当前后两次函数值变化绝对值小于阈值时,停止迭代
3) 设置固定迭代次数
另外还有一个问题,当用户-项目评分矩阵R非常稀疏时,就会出现过拟合(overfitting)的问题,过拟合问题的解决方法就是正则化(regularization)。正则化其实就是在目标函数中加上用户因子向量和项目因子向量的二范数,当然也可以加上一范数。至于加上一范数还是二范数要看具体情况,一范数会使很多因子为0,从而减小模型大小,而二范数则不会它只能使因子接近于0,而不能使其为0,关于这个的介绍可参考论文Regression Shrinkage and Selection via the Lasso。引入正则化项后目标函数变为:
(5)中λ_1和λ_2是指正则项的权重,这两个值可以取一样,具体取值也需要根据数据集调参得到。优化方法和前面一样,只是梯度公式需要更新一下。
矩阵分解算法目前在推荐系统中应用非常广泛,对于使用RMSE作为评价指标的系统尤为明显,因为矩阵分解的目标就是使RMSE取值最小。但矩阵分解有其弱点,就是解释性差,不能很好为推荐结果做出解释。