人工智能新技术——联邦学习的前世今生(下)
文章目录
- 导读
- 密码技术的那些事儿
- 联邦学习的加密原理
- 结语
- 往期回顾
导读
上篇内容回顾:
在《人工智能新技术:联邦学习的前世今生》上篇和中篇里,我们与大家一起揭开了联邦学习的神秘面纱,探索了联邦学习成为解决隐私数据保护和数据共享矛盾的关键技术背后的原因,以及联邦学习应用的前景、难点和实施方式。
本篇为您解读:
- 密码技术的那些事儿
- 联邦学习的加密原理
如前文所述,联邦学习是一种隐私保护的分布式机器学习技术。其中,隐私保护是联邦学习的关键,这是因为传统的分布式机器学习虽然可以实现联邦成员之间的大数据建模,但是容易被黑客破解,导致⽤⼾隐私泄露。密码技术是最常见、最有效的隐私保护方法,可以兼顾数据的可用性和隐私安全性。
密码技术的那些事儿
密码(crypto)的概念由来已久,但与我们的手机解锁“密码”或者WiFi“密码”不同。这些由我们自己设置、用来验证身份的数字或者字母的组合,并非真正意义上的密码,而是“口令”(password)。与简单的口令相比,密码技术则是指通信过程中的一种混淆技术,将明文的消息转变为第三方不可识别的消息,在通信过程被窃听时,防止消息的机密性被泄露。准确地来说,密码技术将明文消息加密成密文,发送给通信的接收方,接收方在收到密文后使用密钥进行解密,从而恢复明文。

然而,看似复杂的密码其实并不神秘,反而与我们的生活息息相关。
电影《唐伯虎点秋香》中的一首"我爱秋香"便是一种安全性较弱的“密码”,将真实含义(明文)隐藏在每句诗的头部,这种隐藏的逻辑便可视为密码系统中的“密钥”,不知道这个逻辑的人看到的只是一首刻画风景的诗(密文),从而起到了隐藏“话外之音”的作用。
由此可见,密码对我们来说并不陌生。它源于人类生活中对隐私和机密性的需求,最终也发展成为了一门系统的科学,服务于人类的社会活动。纵观密码学的发展,可将其大致分为两个阶段:古典密码学和现代密码学。其中现代密码学又可分为两个分支:对称密码学和公钥密码学。
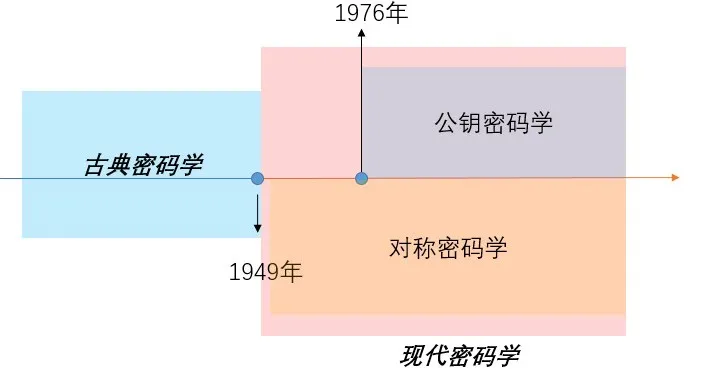
古典密码学的历史可以追溯到古罗马时期,凯撒大帝曾将简单的字母移位方法作为加密手段,用于军事活动中,保护战时通信的机密性。该方案被称为凯撒密码。由于凯撒密码中所有的字母移位的顺序和位数都是相同的,其破译难度较低,为了提高安全性,在凯撒密码的基础上演变出了维吉尼亚密码,在字母移位时,不同的字母进行不同数量的移位,从而降低了使用密文统计特性进行破译的风险。

以凯撒密码和维吉尼亚密码为代表的移位密码体制,其构造都十分简单,但人工计算时难免容易出错,且效率较低。20世纪20年代,人们开始使用机械设备自动处理加密。比如二战时期德军使用的Enigma密码机,给盟军的密码破译工作带来了很大的难度。

随着人们对密码方法的研究逐渐深入,密码攻击手段也越来越多,另外由于计算机的出现以及人类计算能力的大幅提升,古典密码方法的安全性已经不能满足现代人类的需求。但是,古典密码学的不断发展,为密码学的进一步研究提供了思路。
1949年Shannon发表了《保密系统的信息理论》一文,这标志着密码学的研究进入了现代密码学阶段。从此,密码学不再是一门艺术,而成为了一门系统的科学进入了人们的视野。如上文所说,现代密码学又可以分为两个分支:对称密码学和公钥密码学。而1976年则是现代密码学发展过程中一个重要的时间节点。
1976年之前,现代密码学的研究主要集中在对称密码学方向。所谓“对称”,是指加密方和解密方使用的是同一个密钥。在对称密码学后续的研究中,出现了两个较为著名的对称密码方案,分别为DES密码体制和AES密码体制。由于计算能力的提升,目前暴力破解DES成为了可能,因此AES代替了DES成为了新的加密标准并沿用至今。
尽管以AES为代表的对称密码方案有着足够高的安全性,但由于加解密的双方使用共同的密钥,如何让双方在不安全的信道上共享这一密钥,是对称密码学面临的一个问题。1976年Diffie-Hellman密钥交换协议的提出,为这一问题提供了解决思路,同时标志着密码学的新方向——公钥密码学的诞生,将现代密码学的研究带入了一个全新的发展阶段。
公钥密码学又称为非对称密码学,顾名思义,加解密的双方不再使用同一个密钥。其中加密方使用公开的公钥对明文消息进行加密,在解密方收到密文后,使用私钥进行解密。由于私钥只有解密方持有,因此即使存在恶意敌手窃听到了密文,也无法获得明文的信息。典型的公钥密码方案包括RSA、Paillier等经典的方案,以及目前在学术界广受关注的基于格的后量子密码方案等等。
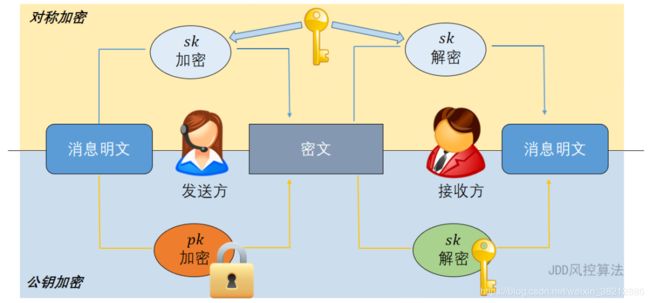
对称密码方案和公钥密码方案的区别不仅仅在于加解密的密钥是否相同。由于两类方案使用不同的加密体制,其应用场景也有着明显的区别。一般来说,由于对称密码方案加解密效率较高,经常应用于文件和数据的批量加密,而公钥密码方案通常有着密钥冗长和效率较低等特点,多应用于密钥分发和数字签名等功能性设计中。
另外,在公钥密码学的发展过程中,也出现了两个重要的分支,即全同态加密和安全多方计算。这两个密码学的分支不仅为传统的机器学习提供了新的发展方向,也为很多复杂业务场景的实现提供了思路。
联邦学习的加密原理
我们知道,机器学习一般使用梯度下降算法实现模型的最优化,联邦学习也是如此。梯度可表示(或者近似)为加法和乘法的混合运算,因此联邦学习的本质需求是加法和乘法运算进行保护。
如前所述,同态加密技术可满足该需求。具体来说,对数据进行同态加密所获得密文可进行加法和乘法操作,结果解密后与数据直接进行加法和乘法的结果是一致的。其中,同时满足加法和乘法的方法称为全同态加密,只能满足其中一种(加法或者乘法)的称为半同态加密。由于全同态加密计算复杂度特别高,联邦学习一般使用半同态加密,比较常见的是Paillier半同态加密,满足如下性质的加法同态:
![]()
有了这两个性质,就可以解决分布式学习所需的各种隐私保护计算了,例如基于梯度下降的迭代优化。以包含两个成员(A和B)的联邦线性回归场景为例, A方的梯度计算式核心部分如下:
上式包含加法和乘法两种运算,可使用加法同态和数乘同态实现。值得注意的是,这里的加密还具有非对称加密的性质,密码包括<公钥,私钥>,使用公钥加密的数据只能通过对应的私钥解密。表示用A的公钥加密,这个公钥会共享给联邦成员,联邦成员可以使用这个公钥对数据进行加密,得到的密文只能由A通过自己的私钥加密;同理,使用B的公钥加密得到的密文只能由B解密。
式子(3)可分级为如下步骤进行计算。

针对线性回归模型,联邦学习梯度下降算法的交互过程(A方)如下图所示。
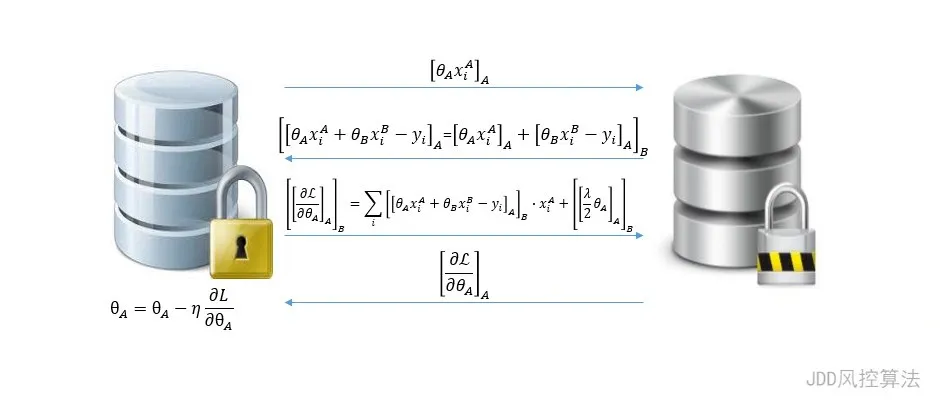
B方的梯度下降迭代与此类似,感兴趣的读者可以此作为参考进行推导。从上面的例子可以看出,联邦学习仅需在联邦之间传输经过半同态加密的中间计算结果,确保了原始数据不出库;同时由于半同态加密破坏了数据的连续性和分布特性,这使得黑客破解成为不可能。
参考文献
[1] Andrew Hard et., al. Federated Learning for Mobile Keyboard Prediction, https://arxiv.org/abs/1811.03604
[2] Qiang Yang et., al. Federated Machine Learning: Concept and Applications. ACM TIST2019. https://arxiv.org/abs/1902.04885
[3] Federated Learning: Collaborative Machine Learning without Centralized Training. https://ai.googleblog.com/2017/04/federated-learning-collaborative.html
[4] Kewei Cheng, Qiang Yang et., al… SecureBoost: A Lossless Federated Learning Framework. https://arxiv.org/abs/1901.08755
[5] 刘洋, 范涛. 联邦学习的研究与应用. https://img.fedai.org.cn/fedweb/1553845987342.pdf
[6] Tian Li et., al. Federated Learning: Challenges, Methods, and Future Directions. https://arxiv.org/abs/1908.07873
[7] 飞向未来的埃舍尔. 联邦学习/联盟学习的发展现状及前景如何?https://www.zhihu.com/question/329518273/answer/717840293
[8] 科学大家|保护信息安全的密码 背后的原理你真懂吗?
https://tech.sina.com.cn/scientist/2019-03-01/doc-ihrfqzka5463594.shtml
[9] 二战德军密码机- Enigma
http://www.boy-toy.net/thread-80044-1-1.html
结语
移动互联网时代的数据共享是一个博弈问题,一方面需要多方合作数据能力提升服务水平,另一方面又需要防止数据泄露造成法律责任和资产损失。密码和联邦学习提供了一种解决方案,通过技术手段提供足够的信任,完全不必猜疑,使得任意企业之间能够形成联邦合作。大家有问题或者有感兴趣的话题,欢迎留言~JDD风控君会尽量满足大家的!
该文章首发于公众号JDD风控算法,点击链接阅读原文
往期回顾
人工智能新技术:联邦学习的前世今生(上)
人工智能新技术:联邦学习的前世今生(中)
想要获取更多资讯,请扫码关注 JDD风控算法