连续信号(四) | 周期信号的频谱分析 | 功率分配 + 傅里叶级数近似
(三)周期信号的功率分配
幅度有限的周期信号是功率信号,如果把信号 x ( t ) x(t) x(t)视为加在 1 Ω 1\Omega 1Ω电阻两端的电压或通过的电流,那么电阻上消耗的平均功率为
p = 1 T 0 ∫ − T 0 2 T 0 2 x 2 ( t ) d t p=\frac{1}{T_0}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x^2(t)dt p=T01∫−2T02T0x2(t)dt
将 x ( t ) = A 0 2 + ∑ n = 1 ∞ A n c o s ( n w 0 t + φ n ) x(t)=\frac{A_0}{2}+\sum_{n=1}^{\infty}A_ncos(nw_0t+\varphi_n) x(t)=2A0+∑n=1∞Ancos(nw0t+φn)代入,并考虑余弦函数集的正交性,有
p = 1 T 0 ∫ − T 0 2 T 0 2 [ A 0 2 + ∑ n = 1 ∞ A n c o s ( n w 0 t + φ n ) ] 2 d t = ( A 0 2 ) 2 + ∑ n = 1 ∞ 1 2 A n 2 p=\frac{1}{T_0}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}[\frac{A_0}{2}+\sum_{n=1}^{\infty}A_ncos(nw_0t+\varphi_n)]^2dt=(\frac{A_0}{2})^2+\sum_{n=1}^{\infty}\frac{1}{2}A_n^2 p=T01∫−2T02T0[2A0+n=1∑∞Ancos(nw0t+φn)]2dt=(2A0)2+n=1∑∞21An2
上式表明周期信号在时域的平均功率等于信号所包含的直流、基波及各次谐波的平均功率之和,反映了周期信号的平均功率对离散频率的分配关系,称为功率信号的帕斯瓦尔公式。如果参照周期信号的幅度频谱,将各次谐波(包括直流)的平均功率分配关系表示成谱线形式,就得到周期信号的功率频谱。
(四)周期信号的傅里叶级数近似
无论是三角傅里叶级数形式,还是指数傅里叶级数形式,都表明了在一般情况下一个周期信号是由无穷多项正弦型信号(直流、基波及各项谐波)组合而成,换言之,一般情况下,无穷多项正弦型信号的和才能完全逼近一个周期信号。如果采用有限项级数表示周期信号,势必产生表示误差。
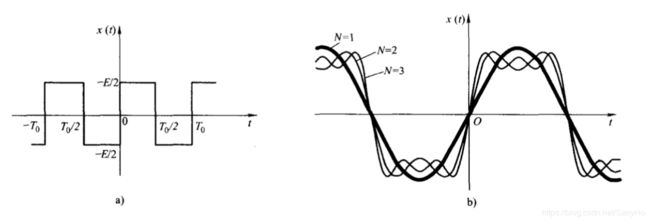
例5:周期方波信号的三角形傅里叶级数展开式
x ( t ) = { − E 2 − T 0 2 ≤ t < 0 E 2 0 ≤ t < T 0 2 x(t)= \begin{cases} -\frac{E}{2} & -\frac{T_0}{2}\leq t<0 \\ \frac{E}{2} & 0\leq t<\frac{T_0}{2} \end{cases} x(t)={−2E2E−2T0≤t<00≤t<2T0
a n = 2 T 0 ∫ − T 0 2 T 0 2 x ( t ) c o s n w 0 t d t = 2 T 0 ( − E 2 ) 1 n w 0 [ s i n n w 0 t ] ∣ − T 0 2 0 + 2 T 0 ( − E 2 ) 1 n w 0 [ s i n n w 0 t ] ∣ 0 T 0 2 a_n=\frac{2}{T_0}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}x(t)cosnw_0tdt \\ =\frac{2}{T_0}(-\frac{E}{2})\frac{1}{nw_0}[sinnw_0t]|_{-\frac{T_0}{2}}^0+\frac{2}{T_0}(-\frac{E}{2})\frac{1}{nw_0}[sinnw_0t]|^{\frac{T_0}{2}}_0 an=T02∫−2T02T0x(t)cosnw0tdt=T02(−2E)nw01[sinnw0t]∣−2T00+T02(−2E)nw01[sinnw0t]∣02T0
考虑到 w 0 = 2 π T 0 w_0=\frac{2\pi}{T_0} w0=T02π,可得
a n = 0 n = 0 , 1 , 2 , ⋯ a_n=0 \quad n=0,1,2,\cdots an=0n=0,1,2,⋯
b n = 2 T 0 ∫ − T 0 2 T 0 2 x ( t ) x i n n w 0 t d t = { 2 E n π n = 1 , 3 , 5 , ⋯ 0 n = 2 , 4 , 6 , ⋯ b_n=\frac{2}{T_0}\int^\frac{T_0}{2}_{-\frac{T_0}{2}}x(t)xin\,nw_0tdt \\ =\begin{cases} \frac{2E}{n\pi} & n=1,3,5,\cdots \\ 0 & n=2,4,6,\cdots \end{cases} bn=T02∫−2T02T0x(t)xinnw0tdt={nπ2E0n=1,3,5,⋯n=2,4,6,⋯
所以 x ( t ) x(t) x(t)的三角形傅里叶级数展开式为
x ( t ) = 2 E π ( s i n w 0 t + 1 3 s i n 3 w 0 t + 1 5 s i n 5 w 0 t + ⋯ ) x(t)=\frac{2E}{\pi}(sinw_0t+\frac{1}{3}sin3w_0t+\frac{1}{5}sin5w_0t+\cdots) x(t)=π2E(sinw0t+31sin3w0t+51sin5w0t+⋯)
上式表明所示的周期方波含有与原信号相同频率的正弦信号、频率为原信号频率3倍的正弦信号,以及频率为原信号频率其它奇数倍的正弦信号,而各正弦波的幅值随频率的增大而成比例减小。
若取傅里叶级数的前N项来逼近周期方波信号 x ( t ) x(t) x(t),则 x N ( t ) x_N(t) xN(t)为
x N ( t ) = ∑ n = 1 N b 2 n − 1 s i n ( 2 n − 1 ) w 0 t x_N(t)=\sum_{n=1}^Nb_{2n-1}sin(2n-1)w_0t xN(t)=n=1∑Nb2n−1sin(2n−1)w0t
引起的误差函数为
ϵ N ( t ) = x ( t ) − x N ( t ) \epsilon_N(t)=x(t)-x_N(t) ϵN(t)=x(t)−xN(t)
均方误差为
ϵ N 2 ( t ) ‾ = 1 T 0 ∫ − T 0 2 T 0 2 ϵ N 2 ( t ) d t = E 2 4 − 1 2 ∑ n = 1 N b 2 n − 1 2 \overline{\epsilon^2_N(t)}=\frac{1}{T_0}\int_{-\frac{T_0}{2}}^{\frac{T_0}{2}}\epsilon^2_N(t)dt=\frac{E^2}{4}-\frac{1}{2}\sum_{n=1}^Nb^2_{2n-1} ϵN2(t)=T01∫−2T02T0ϵN2(t)dt=4E2−21n=1∑Nb2n−12
其中N=1为只取基波一项时的波形,这时均方误差为
ϵ 1 2 ( t ) ‾ = E 2 4 − 1 2 ( 2 E π ) 2 ≈ 0.05 E 2 \overline{\epsilon_1^2(t)}=\frac{E^2}{4}-\frac{1}{2}(\frac{2E}{\pi})^2 \approx 0.05E^2 ϵ12(t)=4E2−21(π2E)2≈0.05E2
其中N=2为取基波和三次谐波时的波形,这时均方误差为
ϵ 3 2 ( t ) ‾ = E 2 4 − 1 2 [ ( 2 E π ) 2 + ( 2 E 3 π ) 2 ] ≈ 0.02 E 2 \overline{\epsilon_3^2(t)}=\frac{E^2}{4}-\frac{1}{2}[(\frac{2E}{\pi})^2+(\frac{2E}{3\pi})^2] \approx 0.02E^2 ϵ32(t)=4E2−21[(π2E)2+(3π2E)2]≈0.02E2
可以看出:傅里叶级数所取项数越多,叠加后波形越逼近原信号,两者之间均方误差越小。显然,当 N → ∞ , x N ( t ) → x ( t ) N\to \infty,x_N(t)\to x(t) N→∞,xN(t)→x(t);当信号 x ( t ) x(t) x(t)为方波等脉冲信号时,其高频分量主要影响脉冲的跳变沿,低频分量主要影响脉冲的顶部,所以, x ( t ) x(t) x(t)波形变化俞激烈,所包含的高频分量愈丰富;变化俞缓慢,所包含的低频分量愈丰富;组成原信号 x ( t ) x(t) x(t)的任一频谱分量(包括幅值、相位)发生变化时,信号 x ( t ) x(t) x(t)的任一频谱分量(包括幅值、相位)发生变化时,信号 x ( t ) x(t) x(t)的波形也会发生变化。