深度学习(二十一)——SRCNN, DRCN, VDSR
https://antkillerfarm.github.io/
图像超分辨率算法(续)
前DL时代的SR
从信号处理的角度来说,LR之所以无法恢复成HR,主要在于丢失了图像的高频信息。(Nyquist采样定理)
Harry Nyquist,1889~1976,University of North Dakota本硕(1914,1915)+耶鲁博士(1917)。AT&T贝尔实验室电子工程师。IEEE Medal of Honor获得者(1960)。
IEEE Medal of Honor是IEEE的最高奖,除了1963年之外,每年只有1人得奖,个别年份甚至会轮空。
最简单的当然是《图像处理理论(二)》中提到的梯度锐化和拉普拉斯锐化,这种简单算法当然不要指望有什么好效果,聊胜于无而已。这是1995年以前的主流做法。
稍微复杂的方法,如同CV的其它领域经历了“信号处理->ML->DL”的变迁一样,SR也进入了ML阶段。
上图是两种典型的SR算法。
左图算法的中心思想是从图片中找出相似的大尺度区域,然后利用这个大区域的边缘信息进行SR。但这个方法对于那些只出现一次的边缘信息是没什么用的。
于是就有了右图的算法。对各种边缘信息建立一个数据库,使用时从数据库中挑一个最类似的边缘信息进行SR。这个方法比上一个方法好一些,但不够鲁棒,图片稍作改动,就有可能无法检索到匹配的边缘信息了。
ML时代的代表算法还有:
《Image Super-Resolution via Sparse Representation》
这篇论文是黄煦涛和马毅小组的Jianchao Yang的作品。
黄煦涛(Thomas Huang),1936年生。生于上海,国立台湾大学本科(1956)+MIT硕博(1960,1963)。UIUC教授。美国工程院院士,中国科学院+中国工程院外籍院士。
马毅,清华本科(1995)+UCB硕博(1997,2000)。UCB教授。IEEE fellow。
个人主页:
http://yima.csl.illinois.edu/
这篇论文提出的算法,在形式上和后文这些DL算法已经非常类似了,也是基于HR和LR配对的有监督训练。区别只在于这篇论文使用矩阵的稀疏表示来拟合SR函数,而DL算法使用神经网络拟合SR函数。前者是线性变换,而后者是非线性变换。
参考
https://zhuanlan.zhihu.com/p/25532538
深度学习在图像超分辨率重建中的应用
https://zhuanlan.zhihu.com/p/25201511
深度对抗学习在图像分割和超分辨率中的应用
https://mp.weixin.qq.com/s/uK0L5RV0bB2Jnr5WCZasfw
深度学习在单图像超分辨率上的应用:SRCNN、Perceptual loss、SRResNet
https://mp.weixin.qq.com/s/xpvGz1HVo9eLNDMv9v7vqg
NTIRE2017夺冠论文:用于单一图像超分辨率的增强型深度残差网络
https://www.zhihu.com/question/25401250
如何通过多帧影像进行超分辨率重构?
https://www.zhihu.com/question/38637977
超分辨率重建还有什么可以研究的吗?
https://zhuanlan.zhihu.com/p/25912465
胎儿MRI高分辨率重建技术:现状与趋势
https://mp.weixin.qq.com/s/i-im1sy6MNWP1Fmi5oWMZg
华为推出新型HiSR:移动端的超分辨率算法
SRCNN
SRCNN(Super-Resolution CNN)是汤晓鸥小组的Chao Dong的作品。
汤晓鸥,中国科学技术大学本科(1990)+罗切斯特大学硕士(1991)+麻省理工学院博士(1996)。香港中文大学教授,商汤科技联合创始人。
论文:
《Learning a Deep Convolutional Network for Image Super-Resolution》
该方法对于一个低分辨率图像,先使用双三次(bicubic)插值将其放大到目标大小,再通过三层卷积网络做非线性映射,得到的结果作为高分辨率图像输出。作者将三层卷积的结构解释成与传统SR方法对应的三个步骤:图像块的提取和特征表示,特征非线性映射和最终的重建。
三个卷积层使用的卷积核的大小分为为9x9, 1x1和5x5,前两个的输出特征个数分别为64和32。
以下是论文的效果表格:
吐槽一下,这种表格属于论文必须有,但是却没什么营养的部分,且不乏造假的例子。原因很简单,一个idea,如果没有好效果,paper连发都发不了。但是,没有好效果的idea,未必没有价值,不说是否能启发人们的思维,至少能让后来者,不用再掉到同一个坑里。
比如化学领域,失败的实验远远多于成功的实验。在计算能力不发达的时代,人们主要关注成功的案例,但现在大家逐渐意识到:失败的案例才是更大的财富。
这里对其中的指标做一个简介。
PSNR(Peak Signal to Noise Ratio,峰值信噪比)
其中,MSE表示当前图像X和参考图像Y的均方误差(Mean Square Error),H、W分别为图像的高度和宽度;n为每像素的比特数,一般取8,即像素灰阶数为256. PSNR的单位是dB,数值越大表示失真越小。
虽然PSNR和人眼的视觉特性并不完全一致,但是一般认为PSNR在38以上的时候,人眼就无法区分两幅图片了。
SSIM(structural similarity, 结构相似性),也是一种全参考的图像质量评价指标,它分别从亮度、对比度、结构三方面度量图像相似性。
C1,C2,C3 C 1 , C 2 , C 3 为常数,为了避免分母为0的情况,通常取 C1=(K1⋅L)2,C2=(K2⋅L)2,C3=C2/2 C 1 = ( K 1 ⋅ L ) 2 , C 2 = ( K 2 ⋅ L ) 2 , C 3 = C 2 / 2 ,一般地 K1=0.01,K2=0.03,L=255 K 1 = 0.01 , K 2 = 0.03 , L = 255 。
SSIM取值范围[0,1],值越大,表示图像失真越小。
在实际应用中,可以利用滑动窗将图像分块,令分块总数为N,考虑到窗口形状对分块的影响,采用高斯加权计算每一窗口的均值、方差以及协方差,然后计算对应块的结构相似度SSIM,最后将平均值作为两图像的结构相似性度量,即平均结构相似性MSSIM:
需要指出的是,PSNR和SSIM都是一些物理指标,它和人眼的视觉感受有一定的差异,不见得指标差的图就一定不如指标好的图(比如SRGAN)。
主观得分一般采用MOS(mean opinion score)作为评价指标。
参考:
http://blog.csdn.net/u011692048/article/details/77496861
超分辨率重建之SRCNN
http://www.cnblogs.com/vincent2012/archive/2012/10/13/2723152.html
PSNR和SSIM
DRCN
DRCN(deeply-recursive convolutional network)是韩国首尔国立大学的作品。
论文:
《Deeply-Recursive Convolutional Network for Image Super-Resolution》
SRCNN的层数较少,同时感受野也较小(13x13)。DRCN提出使用更多的卷积层增加网络感受野(41x41),同时为了避免过多网络参数,该文章提出使用递归神经网络(RNN)。网络的基本结构如下:
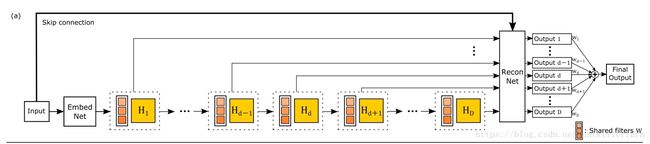
与SRCNN类似,该网络分为三个模块,第一个是Embedding network,相当于特征提取,第二个是Inference network, 相当于特征的非线性变换,第三个是Reconstruction network,即从特征图像得到最后的重建结果。其中的Inference network是一个递归网络,即数据循环地通过该层多次。将这个循环进行展开,就等效于使用同一组参数的多个串联的卷积层,如下图所示:
其中的 H1 H 1 到 HD H D 是D个共享参数的卷积层。DRCN将每一层的卷积结果都通过同一个Reconstruction Net得到一个重建结果,从而共得到D个重建结果,再把它们加权平均得到最终的输出。另外,受到ResNet的启发,DRCN通过skip connection将输入图像与H_d的输出相加后再作为Reconstruction Net的输入,相当于使Inference Net去学习高分辨率图像与低分辨率图像的差,即恢复图像的高频部分。
参考:
http://blog.csdn.net/u011692048/article/details/77500764
超分辨率重建之DRCN
VDSR
VDSR是DRCN的原班人马的新作。
论文:
《Accurate Image Super-Resolution Using Very Deep Convolutional Networks》
代码:
code:https://github.com/huangzehao/caffe-vdsr
SRCNN存在三个问题需要进行改进:
1、依赖于小图像区域的内容;
2、训练收敛太慢;
3、网络只对于某一个比例有效。
VDSR模型主要有以下几点贡献:
1、增加了感受野,在处理大图像上有优势,由SRCNN的13x13变为41x41。(20层的3x3卷积)
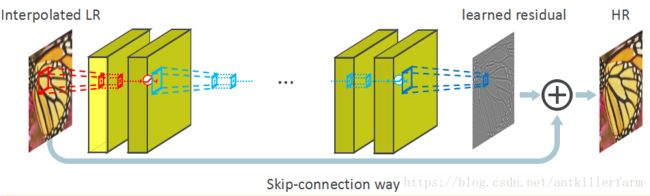
2、采用残差图像进行训练,收敛速度变快,因为残差图像更加稀疏,更加容易收敛(换种理解就是LR携带者低频信息,这些信息依然被训练到HR图像,然而HR图像和LR图像的低频信息相近,这部分花费了大量时间进行训练)。
3、考虑多个尺度,一个卷积网络可以处理多尺度问题。
训练的策略:
1、采用残差的方式进行训练,避免训练过长的时间。
2、使用大的学习进行训练。
3、自适应梯度裁剪,将梯度限制在某一个范围。
4、多尺度,多种尺度样本一起训练可以提高大尺度的准确率。
对于边界问题,由于卷积的操作导致图像变小的问题,本文作者提出一个新的策略,就是每次卷积后,图像的size变小,但是,在下一次卷积前,对图像进行补0操作,恢复到原来大小,这样不仅解决了网络深度的问题,同时,实验证明对边界像素的预测结果也得到了提升。
参考:
http://blog.csdn.net/u011692048/article/details/77512310
超分辨率重建之VDSR