压电式加速度传感器动态特性

压电式加速度传感器动态特性

压电式加速度传感器工作原理如下图所示：

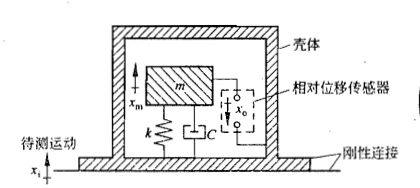
将加速度传感器壳体位移设为$x_1(t)$，质块m运动设为$x_0(t)$，

质块相对于壳体的运动设为$x_{01}(t)$。

压电式加速度传感器的数学模型

依照传感器的力学模型，有达朗贝尔原理可以有以下运动微分方程：
$$m\frac{d^2{x}_0}{d{t}^2}+c(\frac{d{x}_0}{dt}-\frac{d{x}_1}{dt})+k(x_0(t)-x_1(t))$$
压电式传感器系统输入为壳体运动$x_1(t)$，输出为质块m与壳体的相对运动$x_{01}(t)$，此二者的关系为：
$$x_{01}(t)=x_0(t)-x_1(t)$$
于是运动微分方程可以写为：
$$m\frac{d^2{x}_{0}1}{d{t}^2}+c(\frac{d{x}_{01}}{dt})+k{x}_{01}(t)=-m\frac{d^2{x}_1}{d{t}^2}$$
设被测振动为为谐波振动，即有：
$$x_1(t)=X_{1}sin(\omega t)$$
于是运动微分方程：
$$m\frac{d^2{x}_{0}1}{d{t}^2}+c(\frac{d{x}_{01}}{dt})+k{x}_{01}(t)=m{X}_1{\omega }^{2}sin(\omega t)$$
将其写为一般形式为：
$$\frac{d^2{x}_{0}1}{d{t}^2}+2\xi {\omega }_n(\frac{d{x}_{01}}{dt})+{\omega }^2{x}_{01}(t)=X_1{\omega }^{2}sin(\omega t)$$

次微分方程的解由通解和特解两部分组成，其中通解反映此系统的固有特性，特解反映其动态特性；

由于激励为一个正弦信号，因此其响应也为同频率的正弦信号，设其响应为：
$$x_{01}(t)=X_{01}\sin (\omega t+\varphi )$$
于是有：
$$\begin{gathered} \frac{d{x}_{01}}{dt}=\omega X_{01}\cos (\omega t+\varphi )=\omega X_{01}\sin (\omega t+\varphi +\frac{\pi }{2}) \\ \frac{d{x}_{01}^2}{d{t}^2}=-{\omega }^2{X}_{01}\sin (\omega t+\varphi )=\frac{d{x}_{01}^2}{d{t}^2}={\omega }^2{X}_{01}\sin (\omega t+\varphi +\pi ) \end{gathered}$$
按照旋转向量计算，最终得出其响应为：
$$\begin{gathered} A_x(\omega )=\frac{X_{0}1}{X_1}=\frac{(\omega /{\omega }_n)}{\sqrt{[1-(\omega /{\omega }_n{)}^2{]}^2+[2\xi (\omega /{\omega }_n){]}^2}} \\ \varphi (\omega )=\arctan (\frac{2\xi (\omega /{\omega }_n)}{1-(\omega /{\omega }_n{)}^2}) \end{gathered}$$

MATALB绘制幅频特性曲线与相频特性曲线

由于MATLAB中反三角函数$arctan$输出默认为$[-\pi /2,\pi /2]$，因此需要将自定义函数，将其输出改为$[-\pi /2,\pi /2]$，代码为：

function angle = atandpi(x)
%将atand输出更改为0-pi
%   此处显示详细说明
y=atand(x);
L=length(y);
for i=1:L
    if y(i)<0
        y(i)=y(i)+180;
    end
end
angle=y;
end

然后绘制幅频与相频特性曲线，代码为：

%压电式振动传感器的动态特性
clear;
clc;
r=0:0.01:10;
xi=[0,0.3,0.4,0.5,0.6,0.7,1,2,5,10];
%位移幅频特性
Ax1=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(1))*(r)).^2));
Ax2=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(2))*(r)).^2));
Ax3=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(3))*(r)).^2));
Ax4=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(4))*(r)).^2));
Ax5=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(5))*(r)).^2));
Ax6=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(6))*(r)).^2));
Ax7=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(7))*(r)).^2));
Ax8=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(8))*(r)).^2));
Ax9=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(9))*(r)).^2));
Ax10=(r.^2)./sqrt(((1-(r.^2)).^2)+((2*(xi(10))*(r)).^2));
subplot(2,1,1);
plot(r,Ax1,r,Ax2,r,Ax3,r,Ax4,r,Ax5,r,Ax6,r,Ax7,r,Ax8,r,Ax9,r,Ax10);
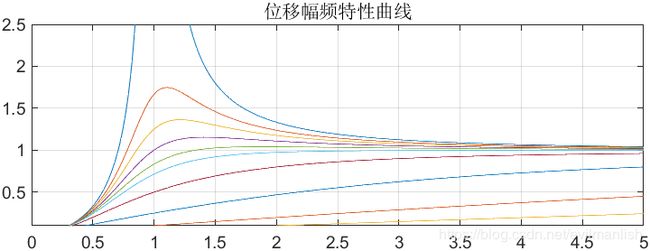
title('位移幅频特性曲线');
xlim([0 5]);
ylim([0.1 2.5]);
grid on;
%相频特性曲线
phi1=atandpi((2*xi(1)*r)./(1-(r.^2)));
phi2=atandpi((2*xi(2)*r)./(1-(r.^2)));
phi3=atandpi((2*xi(3)*r)./(1-(r.^2)));
phi4=atandpi((2*xi(4)*r)./(1-(r.^2)));
phi5=atandpi((2*xi(5)*r)./(1-(r.^2)));
phi6=atandpi((2*xi(6)*r)./(1-(r.^2)));
phi7=atandpi((2*xi(7)*r)./(1-(r.^2)));
phi8=atandpi((2*xi(8)*r)./(1-(r.^2)));
phi9=atandpi((2*xi(9)*r)./(1-(r.^2)));
phi10=atandpi((2*xi(10)*r)./(1-(r.^2)));
subplot(2,1,2);
plot(r,phi1,r,phi2,r,phi3,r,phi4,r,phi5,r,phi6,r,phi7,r,phi8,r,phi9,r,phi10);
title('相频特性曲线');
xlim([0 3])
grid on;
%速度幅频特性

运行结果如下：