半边数据结构与网格细分算法Loop subdivision（附代码）

网格细分的原理其实并不难理解，它的难点主要在于如何实现。在看过无数有原理无代码的博客后，终于决定写一写我的实现方法，并附上代码供大家参考。c++写的可能比较笨拙，望见谅。

1.半边数据结构

很好理解，就是把网格的每一条边分成两个半边，半边是有方向的同一条边的两个半边方向相反。并且一条边是属于两个面，则半边完全属于一个面。

综合上述，得到半边的数据结构为一条半边的起始顶点origin，这条半边指向的下一条半边next，这条半边对应的另外半边opposite，和这条半边所在的面IncFace。

typedef struct HalfEdge//半边结构

{

        int origin;

        struct HalfEdge* next;

        struct HalfEdge* opposite;

        int IncFace;

}HalfEdge;

 

2.网格细分算法Loop subdivision

我只写了三角形网格的细分，即实现了Loop subdivision算法。

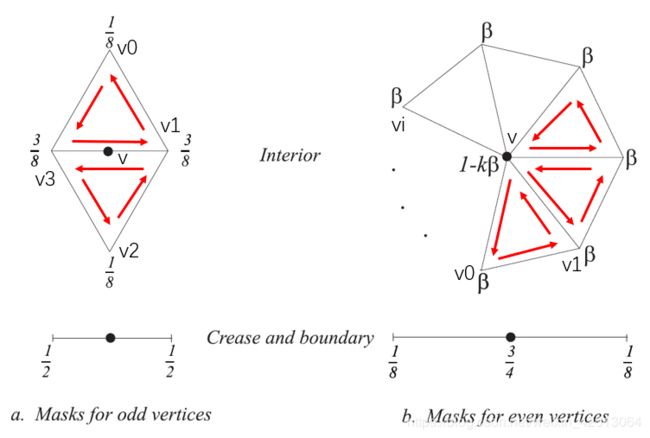
首先，我们应该清楚这个算法是怎样细分的：

​

图中上面两种情况适用于内部点和内部边产生新点的更新，下面两种情况适用于边界点和边界产生新点的更新。

由于我只细分了闭合的三维图形，所以代码只实现了第一种情况，就不讨论第二种了。

细分过程中，

• 每一条边都会产生一个新的顶点，这个顶点由该边所在的两个面中所有顶点决定，即v = 3/8*(v1 + v3) + 1/8*(v0 + v2)
• 每一个原来的顶点都会更新自己的坐标，这个更新由所有与它相邻的原顶点决定，即 ​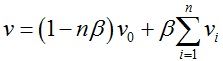，其中 ​

所以，每次细分要做的就是处理每一个旧顶点和每一条边，生成新的顶点，再将新的顶点连接成半边和面。

 

算法思路：

1.读入图形文件，分别定义数据结构保存图形的点，线，面。定义半边数据结构，将所有边转换为半边。然后开始细分。

2.更新旧顶点：第一步，遍历所有半边，找到一条以该顶点为起始顶点的半边。第二步，通过这条半边找到它的next半边，next半边的origin为v1。再找next半边的next半边 的opposite半边，进入下一个面。第三步，重复第二步直到找到的origin点vi等于v1，则已经找到所有vi，可计算出旧顶点的更新后坐标。

3.在每条旧边上生成新顶点：遍历每一条半边，通过半边和半边的opposite边的next与origin找到两个面的所有顶点，计算出新的顶点。

4.已经得到了所有新的顶点，连接它们得到新的半边和面。画出新图，细分完成。

 

大概就是这样了，一些地方不知道是否描述清楚，不清楚的请通过代码自行理解。谢谢~

附：（写于ubuntu16.04，g++编译）

#include   
#include 
#include   
#include 
#include  
#include 
#include 
#include

using namespace std;

#define PI 3.1415926536

typedef struct Vertex
{
	float x,y,z;
}Vertex;

typedef struct Face
{
	int num;
	int order[3];
}Face;

typedef struct HalfEdge//半边结构
{
	int origin;
	struct HalfEdge* next;
	struct HalfEdge* opposite;
	int IncFace;
}HalfEdge;

typedef struct Map
{
	int vs,ve,e;
	
}Map;

static char *filename="cube.off";

vector vertex;
vector face;
vector edge;
int e_num;
int n_node,n_face,n_edge;
int width=800; 
int height=800;

int readoff(const char* filename)
{
	FILE *fp;
	
	if(!(fp=fopen(filename,"r")))
	{
		fprintf(stderr,"Open fail");
		return 0;
	}

    	char buffer[1024];
	if(fgets(buffer,1023,fp))
	{
		if(!strstr(buffer,"OFF"))
		{
			printf("It's not a OFF FILE");
			return 0;
		}
		
		if(fgets(buffer,1023,fp))
		{
			sscanf(buffer,"%d %d %d",&n_node,&n_face,&n_edge);
			
			for(int i=0;iorigin<<" "<next->origin<<" "<origin<<" "<opposite->origin<origin==v)
			return edge[k];
	}
	return NULL;
}

void subdivide()
{
	vector vertex2;
	vector face2;
	vector edge2;
	HalfEdge* he=new HalfEdge();
	int n;
	float p_sumx,p_sumy,p_sumz;
	float px,py,pz;
	float beta;
cout<<"细分开始"<next;
			int p0=e->origin;

			while(e->next->origin!=p0)
			{
				n++;
				p_sumx+=vertex[e->next->origin].x;
				p_sumy+=vertex[e->next->origin].y;
				p_sumz+=vertex[e->next->origin].z;
				HalfEdge* te=new HalfEdge();
				te=e->next->opposite;
				e=te->next;
			}
			n++;
			p_sumx+=vertex[p0].x;
			p_sumy+=vertex[p0].y;
			p_sumz+=vertex[p0].z;
			beta=1/(double)n*(0.625-pow(0.375+0.25*cos(2*PI/n),2));

			px=(1-n*beta)*vertex[i].x+beta*p_sumx;
			py=(1-n*beta)*vertex[i].y+beta*p_sumy;
			pz=(1-n*beta)*vertex[i].z+beta*p_sumz;

			Vertex v;
			v.x=px;
			v.y=py;
			v.z=pz;
			vertex2.push_back(v);
		}
	}
	int map1[n_node][n_node]={0};

cout<<"map1="<origin][edge[i]->next->origin])
		{
			int p=edge[i]->origin;
			int pi=edge[i]->next->origin;
			int pi1=edge[i]->next->next->origin;
			int pi0=edge[i]->opposite->next->next->origin;
			qx=0.375*(vertex[p].x+vertex[pi].x)+0.125*(vertex[pi1].x+vertex[pi0].x);
			qy=0.375*(vertex[p].y+vertex[pi].y)+0.125*(vertex[pi1].y+vertex[pi0].y);
			qz=0.375*(vertex[p].z+vertex[pi].z)+0.125*(vertex[pi1].z+vertex[pi0].z);

			Vertex v;
			v.x=qx;
			v.y=qy;
			v.z=qz;
			vertex2.push_back(v);

			map1[edge[i]->origin][edge[i]->next->origin]=vertex2.size()-1;
			map1[edge[i]->next->origin][edge[i]->origin]=vertex2.size()-1;
		}
	}
/*
cout<<"新点"<origin<<" "<next->origin<<" "<IncFace<

图形文件cube.off

OFF
8 12 0
-0.5 -0.5 -0.5
0.5 -0.5 -0.5
-0.5 0.5 -0.5
0.5 0.5 -0.5
-0.5 -0.5 0.5
0.5 -0.5 0.5
-0.5 0.5 0.5 
0.5 0.5 0.5 
3 4 5 6
3 6 5 7
3 5 1 7
3 7 1 3
3 0 3 1
3 0 2 3
3 4 6 2
3 4 2 0
3 6 7 2
3 3 2 7
3 5 4 0
3 5 0 1