确定有限状态机和非确定有限状态机详解 包含Java实现源码（Nondeterministic finite automata）
本文将讲解确定有限自动状态机和非确定有限自动状态机的特点和区别。将结合图片例子重点讲解什么是非确定有限自动状态机。最后讲解如何将非确定状态机转换为确定的状态机。多图预警！！
有限自动状态机可以分为确定的和不确定的。“确定性”将在下文详讲。“有限”性表示存在一个结束状态。“自动”体现在当前状态能够根据输入符号而转换到下一个状态。这里的“输入符号”在下文中讲到。“状态机”可以理解为对象状态转换规则的定义，根据所定义的状态转换规则，面对不同的输入，系统能够相应地改变自己地状态。
Java实现源码：有限状态机
还可以参考本人另一篇文章： 下推自动机详讲 包含Java实现 Pushdown Automata （PDA）
1.确定有限自动状态机 Deterministic Finite Automata （DFA）
1.1. 特点：
- 在DFA中，给定当前状态，我们能够知道下一个状态。
- 下一个状态是唯一确定的。
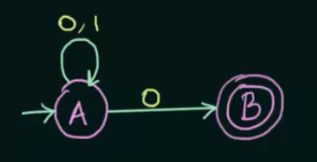
- 从符号空间中选择任意一个符号输入，总有一个唯一确定的下一状态。比如上图中，符号空间为{0，1}，当前状态为A，输入1，那么下一个状态百分之百是B，输入0，为C，其它状态亦然。
- 简单且容易实现。
上图表示一个确定有限自动状态机，其满足上面所列的所有特点。其中A表示初始状态，D被两个圈围住，表示结束状态。数字0和1表示输入符号。状态会根据输入符号而转换下一个状态。
所以根据上面的特点可以确定上图所示的状态机不是确定的有限自动状态机，因为在状态为A的时候，当输入符号为1时没有对应的下一状态。
2.非确定有限自动状态机 Nondeterministic Finite Automata （NFA）
2.1. 特点
- 在NFA中，给定当前状态，可能有多个下一个状态。
- 可以随机选择下一个状态。
- 可以并行（同时）选择下一个状态。
- 输入符号可以为空。
上图表示一个非确定有限自动状态机，其满足上面所列的所有特点。其中A表示初始状态，B,C,D,E表示下一个状态。其中，如果当前状态为A，当输入符号为0的时候，下一状态可能为A或者C。如果输入符号为空，那么下一个状态为E。
下面所展示的所有例子中的输入符号集合的表示空间为{0，1}，其中被字母表示一个状态，被两个圆圈住的状态为结束状态。
3. 非确定有限自动状态（NFA）用例1
上面的图片表示一个NFA，其中所有以0结尾的输入符号集合都满足该状态机，我们使用下面符号表示该符号集合
L={以0结尾的字符串集合}，
比如L={100, 000, 1010, 00, 0}都满足上图所示的状态机。
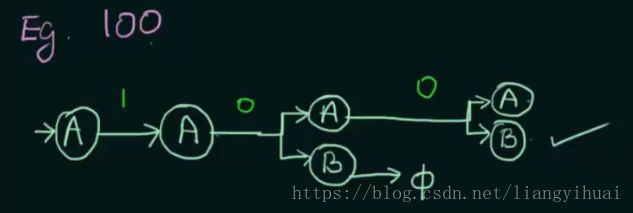
对于该状态机，当输入符号为100的时候，将形成上图所示的状态转换。其中满足输入条件的状态转换为A->A->A->B，所以，100满足该状态机。
再举一个反面的例子，当输入符号为01的时候，是不满足上面状态机的，因为其状态转换将如图下图所示，因为最终的状态不是B。
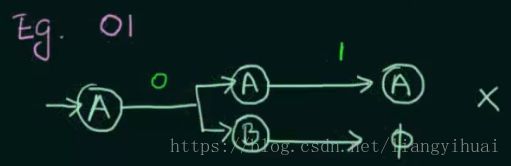
对于上面的例子，我们可以总结一个小小的结论：
对于非确定有限自动状态机，当运行到最后一个输入符号的时候对应的状态中存在“结束状态”，那么该输入符号满足该状态机。其中上面例子中，结束状态为B，如果输入符号为10， 则最后一个输入符号为0.
4. 非确定有限自动状态（NFA）用例2
上面的非确定有限状态机中，L={所有的输入符号都以0开始} 的输入符号都满足。针对该状态机举两个输入例子：
上面图片所示，当输入符号为001的时候，可以展开为上图第一个网络，表示其能够满足该状态机。当输入符号为101的时候，不能满足该状态机，因为其结束状态为空。
是
下面构建一个能够满足输入符号的长度为2并且符号为0或1的非确定有限自动状态机。其中输入符号和该状态机可以表示为：
所以输入符号为00和001的时候，前者满足而后者不满足该状态机。如下图所示。
5. 非确定有限自动状态（NFA）用例3
一个能够满足所有以1结尾的输入符号的非确定有限自动状态机：
一个能够满足所有包含0的输入符号的非确定有限自动状态机：
一个能够满足所有以01开始的输入符号的非确定有限自动状态机：
一个能够满足所有包含01的输入符号的非确定有限自动状态机：
一个能够满足所有以11结尾的输入符号的非确定有限自动状态机：
6.非确定状态机转换为确定状态机
理论表明，（1）所有的DFA都是NFA，反之不然。（2）所有的NFA都能够转换为等价的DFA。
DFA是确定有限自动状态机。NFA是不确定有限自动状态机。
使用表达式表示它们的转换关系为：
其中上面两个等式中箭头表示一个映射，可以理解为一个状态转换函数，字母Q表示一个状态。相同的输入，箭头右边的映射结果不一样。
下面使用一个简单的例子说明如何将非确定有限自动状态机转换为确定的有限自动状态机。非确定的状态机为下图左边所示，其中输入符号的空间为{0，1}。我们使用一个表格把该状态机表示出来，其中当状态为A并且输入符号为1的时候，没有下一状态，为了方便这里使用null表示：
在将上面的非确定状态机转换为确定状态机之前，我们需要做一件事，把上面的状态null表示为状态C，也就是把状态null也看作是一种特殊的状态，现在这个特殊的状态表示为C。那么，我们就可以把上图所示的表格写成下面图片所示的样子了：
相应地我们画出确定的有限自动状态机的网络转换图：
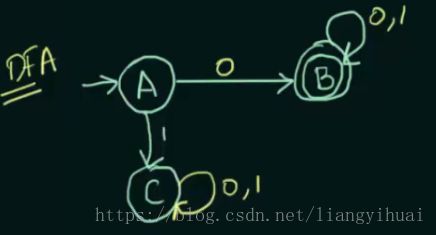
在上面图片中需要注意的是状态C，如果当前状态为C，那么不管输入符号是什么，下一状态都为它本身。这样子就把这个非确定状态机转换为确定状态机了。
谢谢