WGS84与大地2000坐标转换(Java,C#,Dart)
一,WGS84与大地2000坐标互相转换
对于这样的需求我想涉及到jun事,或者电网,农业的项目才会有吧,我们公司的 项目是电网项目,涉及到经纬度和大地2000坐标的转换,当然是App。当时花费了很长时间百度,谷歌,看论文。但是计算结果差很多,没法子最终只能自己看论文且理解原理。Dart,Java,C##版本代码都有自己做了工具类。这里我提供Dart版本。
二,我国三大常用坐标系
我国三大常用坐标系区别(北京54、西安80和WGS-84)我国三大常用坐
标系区别(北京54、西安80和WGS-84)。
1、北京54坐标系(BJZ54)
北京54坐标系为参心大地坐标系
北京54坐标系,属三心坐标系,长轴6378245m,短轴6356863,扁率1/298. 3;
2、西安80坐标系
1978年4月在西安召开全国天文大地网平差会议,确定重新定位,建立我国新的坐标系。(即1985国家高程基准)。西安80坐标系,属三心坐标系,长轴6378140m。
3、WGS-84坐标系(World Geodetic System) 是-种国际上采用的地心坐标系。
坐标原点为地球质心,其地心空间直角坐标系的Z轴指向国际时间局(BIH)WGS84坐标系,长轴6378137. 000m,短轴6356752.314,扁率1/298. 257223563。由于采用的椭球基准不一样,并且由于投影的局限性,使的全国各地并不存在一至的转换参数。对于这种转换由于量较大,有条件的话,一般都采用GPS联测己知点,应用GPS软件自动完成坐标的转换。当然若条件不许可,且有足够的重
合点,也可以进行人工解算。
4、2000 国家大地坐标系
英文缩写为CGCS2000。2000国家大地坐标系是全球地心坐标系在我国的具
体体现,其原点为包括海洋和大气的整个地球的质量中心。2000国家大地坐标
系采用的地球椭球参数如下:
长半轴a=6378137m, 扁率f=1/298.257222101,
地心引力常数GM=3. 986004418X 1014m3s-2
自转角速度w=7.292115X 10-5rads- 1
参考资料:
2000国家大地坐标系
中央子午线经度的计算
WGS84 经纬度坐标到北京 54 高斯投影坐标的转换
4,注意点:
1.明确是WGS8和那个坐标系转换,确定参数值影响很大
大地2000的参数:
double a = 6378137; //椭球长半轴
double b = 6356752.3142451795; //椭球短半轴
double e = 0.081819190842621; //第一偏心率
double eC = 0.0820944379496957; //第二偏心率
对应的其他坐标系自己可以百度。
2.明确自己项目点经纬度所在的带号计算出带所在的中央带经度
这里自己可以百度看看,我国有两种分带,3度带,6度带。
360度=3度X. => X=120份
360度=6度Y => Y=60份
360度=2π弧度
每度=2π/360=π/180
地球是圆的,如上图东西分界线为0度,左右分为东经西经,如果是三分带,那么可以知道,-1.5度(即西经)和 1.5度(即东经)之间的夹角就是3度。1.5到4.5之间和-4.5度(西经)到-1.5(西经)之间是关于子午线对称的,所以经度纬度相等的有两个。我们大地坐标一般避免经度为负都会将平面地图坐标系向左平移500公里。如下图。

所谓的项目点所在的中央经度。例如3分带划分,东经1.5度和4.5度之间就是3,同样3.5和6.5之间就是5, 我们项目点东经3.53226,3.74,3.2334348,4.02323,5.023232…那么它的中央经度为带的中点 3。转换为计算机代码,Math.roun(经度/3)*3.
import 'dart:math';
import 'package:luhenchang_plugin/map/bean/latlng.dart';
import 'bean/tuple.dart';
/*
* 关于地图工具
* @作者路很长
* @路很长的博客地址 https://blog.csdn.net/m0_37667770/article/details/80903890
* @路很长github https://github.com/luhenchang/flutter_study
*/
class LonLatAndXY {
//@将WGS84经纬度转为大地2000坐标。我们是国家电网项目数据很精确的了。
//@param B 纬度
//@param L 经度
//@param degree //
//@param withBand 默认=false
//@return
Tuple gps84ToXY(double B, double L, double degree, {withBand = false}) {
List<double> xy = new List();
xy.add(0);
xy.add(0);
double a = 6378137; //椭球长半轴
double b = 6356752.3142451795; //椭球短半轴
double e = 0.081819190842621; //第一偏心率
double eC = 0.0820944379496957; //第二偏心率
double L0 = 0; //中央子午线经度
int n = 0; //带号
if (degree == 6) {
//6度
n = ((L + degree / 2) / degree).round().toInt();
L0 = degree * n - degree / 2;
} else {
//3度
n = (L / degree).round().toInt();
L0 = degree * n;
}
//开始计算
double radB = B * pi / 180; //纬度(弧度)
double radL = L * pi / 180; //经度(弧度)
double deltaL = (L - L0) * pi / 180; //经度差(弧度)
double N = a * a / b / sqrt(1 + eC * eC * cos(radB) * cos(radB));
double C1 = 1.0 +
3.0 / 4 * e * e +
45.0 / 64 * pow(e, 4) +
175.0 / 256 * pow(e, 6) +
11025.0 / 16384 * pow(e, 8);
double C2 = 3.0 / 4 * e * e +
15.0 / 16 * pow(e, 4) +
525.0 / 512 * pow(e, 6) +
2205.0 / 2048 * pow(e, 8);
double C3 = 15.0 / 64 * pow(e, 4) +
105.0 / 256 * pow(e, 6) +
2205.0 / 4096 * pow(e, 8);
double C4 = 35.0 / 512 * pow(e, 6) + 315.0 / 2048 * pow(e, 8);
double C5 = 315.0 / 131072 * pow(e, 8);
double t = tan(radB);
double eta = eC * cos(radB);
double X = a *
(1 - e * e) *
(C1 * radB -
C2 * sin(2 * radB) / 2 +
C3 * sin(4 * radB) / 4 -
C4 * sin(6 * radB) / 6 +
C5 * sin(8 * radB));
xy[0] = X +
N *
sin(radB) *
cos(radB) *
pow(deltaL, 2) *
(1 +
pow(deltaL * cos(radB), 2) *
(5 - t * t + 9 * eta * eta + 4 * pow(eta, 4)) /
12 +
pow(deltaL * cos(radB), 4) *
(61 - 58 * t * t + pow(t, 4)) /
360) /
2;
xy[1] = N *
deltaL *
cos(radB) *
(1 +
pow(deltaL * cos(radB), 2) * (1 - t * t + eta * eta) / 6 +
pow(deltaL * cos(radB), 4) *
(5 -
18 * t * t +
pow(t, 4) -
14 * eta * eta -
58 * eta * eta * t * t) /
120) +
500000; // +n * 1000000;
return new Tuple(xy[0], xy[1]);
}
//@将大地2000转为WGS84
//高斯投影反算为大地平面。
// x,y ,高斯平面坐标点
//L0 通过经纬度来获取中央带所在带的角度
//return B纬度 , L经度
LatLng xyTowgs84(double x, double y, double L0) {
//中央子午线经度
//WGS-84 椭球体参数
double a = 6378137.0; //major semi axis
double efang = 0.0066943799901413; //square of e
double e2fang = 0.0067394967422764; //suqre of e2
y = y - 500000;
//主曲率计算
double m0, m2, m4, m6, m8;
m0 = a * (1 - efang);
m2 = 3.0 / 2.0 * efang * m0;
m4 = efang * m2 * 5.0 / 4.0;
m6 = efang * m4 * 7.0 / 6.0;
m8 = efang * m6 * 9.0 / 8.0;
//子午线曲率计算
double a0, a2, a4, a6, a8;
a0 = m0 + m2 / 2.0 + m4 * 3.0 / 8.0 + m6 * 5.0 / 16.0 + m8 * 35.0 / 128.0;
a2 = m2 / 2.0 + m4 / 2.0 + m6 * 15.0 / 32.0 + m8 * 7.0 / 16.0;
a4 = m4 / 8.0 + m6 * 3.0 / 16.0 + m8 * 7.0 / 32.0;
a6 = m6 / 32.0 + m8 / 16.0;
a8 = m8 / 128.0;
double X = x;
double FBf = 0;
double Bf0 = X / a0, Bf1 = 0;
//计算Bf的值,直到满足条件
while ((Bf0 - Bf1) >= 0.0001) {
Bf1 = Bf0;
FBf = -a2*sin(2*Bf0)/2 +a4*sin(4*Bf0)/4 -a6*sin(6*Bf0)/6 + a8*sin(8*Bf0)/8;
Bf0 = (X-FBf)/a0;
}
double Bf = Bf0;
//计算公式中参数
double Wf = sqrt(1 - efang * sin(Bf) * sin(Bf));
double Nf = a / Wf;
double Mf = a * (1 - efang) / pow(Wf, 3);
double nffang = e2fang * cos(Bf) * cos(Bf);
double tf = tan(Bf);
double B = Bf - tf * y * y / (2 * Mf * Nf) + tf * (5 + 3 * tf * tf + nffang - 9 * nffang * tf * tf) * pow(y, 4) / (24 * Mf * pow(Nf, 3)) - tf * (61 + 90 * tf * tf + 45 * pow(tf, 4)) * pow(y, 6) / (720 * Mf * pow(Nf, 5));
double l = y/(Nf*cos(Bf)) - (1+2*tf*tf+nffang)*pow(y, 3)/(6*pow(Nf, 3)*cos(Bf)) + (5+28*tf*tf +24*pow(tf, 4))*pow(y, 5)/(120*pow(Nf, 5)*cos(Bf));
double L = l + L0;
//转化成为十进制经纬度格式
var array_B =rad2dms(B);
var array_L =rad2dms(L);
double Bdec = dms2dec(array_B);
double Ldec = dms2dec(array_L);
return new LatLng(Bdec, Ldec);
}
double p = 180.0 / pi * 3600;
//通过经纬度来获取中央带所在带的角度
//@param B 纬度
//@param L 经度
//@param N 带[3,6带度]
double gaussLongToDegreen(double B, double L, int N) {
//计算该地区的中央子午线经度
double L00 = (L / 3).round() * 3.toDouble();
double degreen = L00 / 180 * 3.1415926;
return degreen;
}
//将弧度�?�转化为度分��?
dynamic rad2dms(double rad) {
List<int> a = [0,0,0];
double dms = rad * p;
a[0] = (dms / 3600.0).floor();
a[1] = ((dms - a[0] * 3600) / 60.0).floor();
a[2] = ((dms - a[0] * 3600).toInt() - a[1] * 60);
return a;
}
//将度分秒转化为十进制坐标
double dms2dec(dynamic dms) {
double dec = 0.0;
dec = dms[0] + dms[1] / 60.0 + dms[2] / 3600.0;
return dec;
}
}
Java版本也补发一下
package zj.it.bhne.design.myutils.utils;
import com.baidu.mapapi.model.LatLng;
/**
*
* author : luhenchang
* e-mail : [email protected]
* time : 2020/04/23
* desc : 版权所有
* version: 1.0
*
*/
/*
* 关于地图工具
* @作者路很长
* @路很长的博客地址 https://blog.csdn.net/m0_37667770/article/details/80903890
* @路很长github https://github.com/luhenchang/flutter_study
*/
public class MyKrtUtils {
//@将WGS84经纬度转为大地2000坐标。我们是国家电网项目数据很精确的了。
//@param B 纬度
//@param L 经度
//@param degree //
//@param withBand 默认=false
//@return
/**
* @param B 纬度
* @param L 经度
* @param degree //
* @param withBand 默认=false
* @return
*/
public static GaussKrugerProjection.Tuple GetXY(double B, double L, double degree, Boolean withBand) {
double[] xy = {0, 0};
double a = 6378137;//椭球长半轴
double b = 6356752.3142451795;//椭球短半轴
double e = 0.081819190842621;//第一偏心率
double eC = 0.0820944379496957;//第二偏心率
double L0 = 0;//中央子午线经度
int n = 0;//带号
if (degree == 6) {
//6度
n = (int) (Math.round((L + degree / 2) / degree));
L0 = degree * n - degree / 2;
} else {
//3度
n = (int) Math.round(L / degree);
L0 = degree * n;
}
//开始计算
double radB = B * Math.PI / 180;//纬度(弧度)
double radL = L * Math.PI / 180;//经度(弧度)
double deltaL = (L - L0) * Math.PI / 180;//经度差(弧度)
double N = a * a / b / Math.sqrt(1 + eC * eC * Math.cos(radB) * Math.cos(radB));
double C1 = 1.0 + 3.0 / 4 * e * e + 45.0 / 64 * Math.pow(e, 4) + 175.0 / 256 * Math.pow(e, 6) + 11025.0 / 16384 * Math.pow(e, 8);
double C2 = 3.0 / 4 * e * e + 15.0 / 16 * Math.pow(e, 4) + 525.0 / 512 * Math.pow(e, 6) + 2205.0 / 2048 * Math.pow(e, 8);
double C3 = 15.0 / 64 * Math.pow(e, 4) + 105.0 / 256 * Math.pow(e, 6) + 2205.0 / 4096 * Math.pow(e, 8);
double C4 = 35.0 / 512 * Math.pow(e, 6) + 315.0 / 2048 * Math.pow(e, 8);
double C5 = 315.0 / 131072 * Math.pow(e, 8);
double t = Math.tan(radB);
double eta = eC * Math.cos(radB);
double X = a * (1 - e * e) * (C1 * radB - C2 * Math.sin(2 * radB) / 2 + C3 * Math.sin(4 * radB) / 4 - C4 * Math.sin(6 * radB) / 6 + C5 * Math.sin(8 * radB));
xy[0] = X + N * Math.sin(radB) * Math.cos(radB) * Math.pow(deltaL, 2) * (1 + Math.pow(deltaL * Math.cos(radB), 2) * (5 - t * t + 9 * eta * eta + 4 * Math.pow(eta, 4)) / 12 + Math.pow(deltaL * Math.cos(radB), 4) * (61 - 58 * t * t + Math.pow(t, 4)) / 360) / 2;
xy[1] = N * deltaL * Math.cos(radB) * (1 + Math.pow(deltaL * Math.cos(radB), 2) * (1 - t * t + eta * eta) / 6 + Math.pow(deltaL * Math.cos(radB), 4) * (5 - 18 * t * t + Math.pow(t, 4) - 14 * eta * eta - 58 * eta * eta * t * t) / 120) + 500000;// +n * 1000000;
return new GaussKrugerProjection.Tuple(xy[0], xy[1]);
}
//@将大地2000转为WGS84
//高斯投影反算为大地平面。
// x,y ,高斯平面坐标点
//L0 通过经纬度来获取中央带所在带的角度
//return B纬度 , L经度
public LatLng xyTowgs84(double x, double y, double L0) {
//中央子午线经度
//WGS-84 椭球体参数
double a = 6378137.0; //major semi axis
double efang = 0.0066943799901413; //square of e
double e2fang = 0.0067394967422764; //suqre of e2
y = y - 500000;
//主曲率计算
double m0, m2, m4, m6, m8;
m0 = a * (1 - efang);
m2 = 3.0 / 2.0 * efang * m0;
m4 = efang * m2 * 5.0 / 4.0;
m6 = efang * m4 * 7.0 / 6.0;
m8 = efang * m6 * 9.0 / 8.0;
//子午线曲率计算
double a0, a2, a4, a6, a8;
a0 = m0 + m2 / 2.0 + m4 * 3.0 / 8.0 + m6 * 5.0 / 16.0 + m8 * 35.0 / 128.0;
a2 = m2 / 2.0 + m4 / 2.0 + m6 * 15.0 / 32.0 + m8 * 7.0 / 16.0;
a4 = m4 / 8.0 + m6 * 3.0 / 16.0 + m8 * 7.0 / 32.0;
a6 = m6 / 32.0 + m8 / 16.0;
a8 = m8 / 128.0;
double X = x;
double FBf = 0;
double Bf0 = X / a0, Bf1 = 0;
//计算Bf的值,直到满足条件
while ((Bf0 - Bf1) >= 0.0001) {
Bf1 = Bf0;
FBf = -a2 * Math.sin(2 * Bf0) / 2 + a4 * Math.sin(4 * Bf0) / 4 - a6 * Math.sin(6 * Bf0) / 6 + a8 * Math.sin(8 * Bf0) / 8;
Bf0 = (X - FBf) / a0;
}
double Bf = Bf0;
//计算公式中参数
double Wf = Math.sqrt(1 - efang * Math.sin(Bf) * Math.sin(Bf));
double Nf = a / Wf;
double Mf = a * (1 - efang) / Math.pow(Wf, 3);
double nffang = e2fang * Math.cos(Bf) * Math.cos(Bf);
double tf = Math.tan(Bf);
double B = Bf - tf * y * y / (2 * Mf * Nf) + tf * (5 + 3 * tf * tf + nffang - 9 * nffang * tf * tf) * Math.pow(y, 4) / (24 * Mf * Math.pow(Nf, 3)) - tf * (61 + 90 * tf * tf + 45 * Math.pow(tf, 4)) * Math.pow(y, 6) / (720 * Mf * Math.pow(Nf, 5));
double l = y / (Nf * Math.cos(Bf)) - (1 + 2 * tf * tf + nffang) * Math.pow(y, 3) / (6 * Math.pow(Nf, 3) * Math.cos(Bf)) + (5 + 28 * tf * tf + 24 * Math.pow(tf, 4)) * Math.pow(y, 5) / (120 * Math.pow(Nf, 5) * Math.cos(Bf));
double L = l + L0;
//转化成为十进制经纬度格式
double[] array_B = rad2dms(B);
double[] array_L = rad2dms(L);
double Bdec = dms2dec(array_B);
double Ldec = dms2dec(array_L);
return new LatLng(Bdec, Ldec);
}
double p = 180.0 / Math.PI * 3600;
//通过经纬度来获取中央带所在带的角度
//@param B 纬度
//@param L 经度
//@param N 带[3,6带度]
double gaussLongToDegreen(double B, double L, int N) {
//计算该地区的中央子午线经度
double L00 = Math.round((L / 3)) * 3;
double degreen = L00 / 180 * 3.1415926;
return degreen;
}
//将弧度�?�转化为度分��?
double[] rad2dms(double rad) {
double[] a = {0, 0, 0};
double dms = rad * p;
a[0] = Math.floor(dms / 3600.0);
a[1] = Math.floor((dms - a[0] * 3600) / 60.0);
a[2] = (Integer.parseInt((dms - a[0] * 3600) + "") - a[1] * 60);
return a;
}
//将度分秒转化为十进制坐标
double dms2dec(double[] dms) {
double dec = 0.0;
dec = dms[0] + dms[1] / 60.0 + dms[2] / 3600.0;
return dec;
}
}
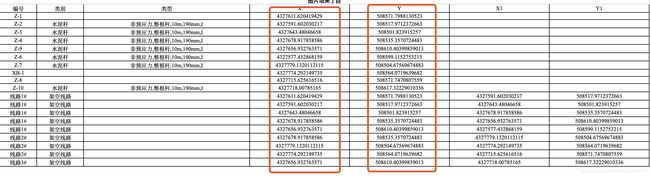
国家电力局rtk测量的如下数据。
看我转换之后的测试了很多都转换为大地2000坐标精确到0.01了。
Tuple{B: 4119992.7554638153, L: 624625.9309849278}
对比 rtf=4119992.756 624625.9311
这紧缺度我怀疑rtf精确度和我们这个差不多。
我们进行大地2000转为WGS84
LatLng{lat: 37.20305555555556, lng: 115.40361111111112}
下面是rtf测量的结果:精确度0.0001了。地图上测试没啥大问题。基本在一点。距离在0.1米内的误差。
37.203267527777776,115.40381543333334
5、最后我封装成库了。
使用
dependencies:
luhenchang_plugin: ^0.1.2
库地址
LonLatAndXY latAndXY=new LonLatAndXY();
Tuple tuple=latAndXY.gps84ToXY(37.203267527777776,115.40381543333334,3);
//我国划分为3或者6分带。这里很多人需要注意。根据你们测量仪器来写。
//我们这个国家电网项目。精确度很好了已经。
double degreen=latAndXY.gaussLongToDegreen(37.203267527777776,115.40381543333334,3);
LatLng latLng=latAndXY.xyTowgs84(4119992.7554638153,624625.9309849278,degreen);
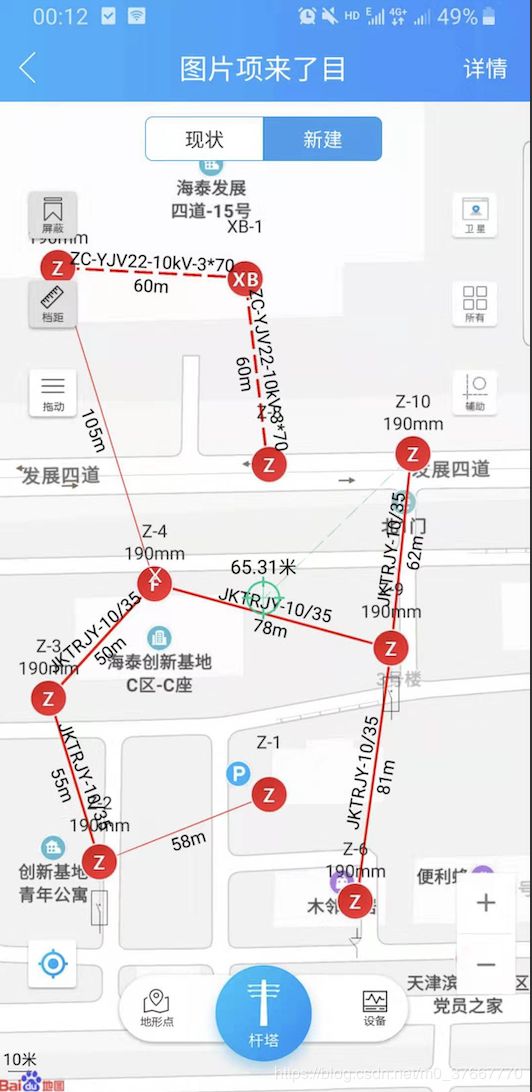
如下App项目使用转换: