机器学习算法:梯度下降法——原理篇
梯度下降法(Gradient Descent,GD)是一种常用的求解
无约束最优化问题的方法,在最优化、统计学以及机器学习等领域有着广泛的应用。本文将深入浅出的为读者介绍梯度下降法的原理。
文章目录
- 1.问题明确
- 2.概念理解
- 3.梯度下降算法原理
- 4.参考文献
1.问题明确
同大家一样,作者在刚听闻梯度下降法这个专业名词的时候也是心中一紧,发出夺命三连问:这是啥?这能干啥?这咋用啊?上面已经提到梯度下降法适用于求解无约束最优化问题,那么什么是无约束最优化问题呢?——不要怕,我们先来看几个你绝对能看懂的例子(当然前提你得有一些统计学和运筹学基础昂,小白先去补课!):
- 形象的例子
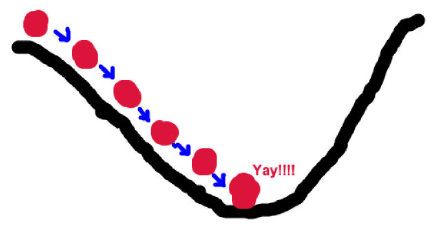
引自Udacity:Gradient Descent - Problem of Hiking Down a Mountain
假设这样一个场景:一个人需要从山的某处开始下山,尽快到达山底。在下山之前他需要确认两件事:
- 下山的方向
- 下山的距离
这是因为下山的路有很多,他必须利用一些信息,找到从该处开始最陡峭的方向下山,这样可以保证他尽快到达山底。此外,这座山最陡峭的方向并不是一成不变的,每当走过一段规定的距离,他必须停下来,重新利用现有信息找到新的最陡峭的方向。通过反复进行该过程,最终抵达山底。
这一过程形象的描述了梯度下降法求解无约束最优化问题的过程,下面我们将例子里的关键信息与梯度下降法中的关键信息对应起来:山代表了需要优化的函数表达式;山的最低点就是该函数的最优值,也就是我们的目标;每次下山的距离代表后面要解释的学习率;寻找方向利用的信息即为样本数据;最陡峭的下山方向则与函数表达式梯度的方向有关,之所以要寻找最陡峭的方向,是为了满足最快到达山底的限制条件;细心的读者可能已经发现上面还有一处加粗的词组:某处——代表了我们给优化函数设置的初始值,算法后面正是利用这个初始值进行不断的迭代求出最优解。
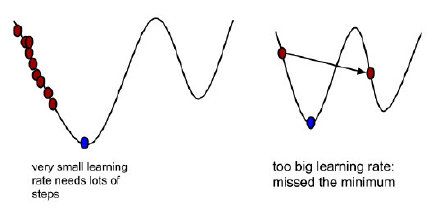
看到这里大家应该会发现这样一个问题:在选择每次行动的距离时,如果所选择的距离过大,则有可能偏离最陡峭的方向,甚至已经到达了最低点却没有停下来,从而跨过最低点而不自知,一直无法到达山底;如果距离过小,则需要频繁寻找最陡峭的方向,会非常耗时。要知道,每次寻找最陡峭的方向是非常复杂的!同样的,梯度下降法也会面临这个问题,因此需要我们找到最佳的学习率,在不偏离方向的同时耗时最短。
- 统计学
经典的回归分析思想是寻找一个回归方程式(也就是自变量x的线性组合),能够最小化平方损失函数:
min β L ( y , f ( x ; β ) ) = ∑ i = 1 n ( y − f ( x ; β ) ) 2 \min _ { \beta } L ( y , f ( x ; \beta ) ) = \sum _ { i = 1 } ^ { n } ( y - f ( x ; \beta ) ) ^ { 2 } βminL(y,f(x;β))=i=1∑n(y−f(x;β))2
上式可以看作一个典型的无约束最优化问题,自变量x与因变量y均由数据给出,n为样本个数, β \beta β为待估参数(既回归系数)。最小二乘法是求解回归系数最常用的方法之一,系数 β \beta β的解析解为(矩阵表达):
β ^ = ( X ⊤ X ) − 1 X ⊤ Y \hat { \beta } = \left( X ^ { \top } X \right) ^ { - 1 } X ^ { \top } Y β^=(X⊤X)−1X⊤Y
注意,在上面的表达式中需要对矩阵求逆,而只有当一个矩阵是非奇异矩阵(既可逆矩阵)时才存在逆运算。当矩阵 ( X ⊤ X ) \left ( X^{\top } X\right ) (X⊤X)是奇异矩阵,常规的最小二乘法便会失效。另外要说的是,一般情况下我们所用的数据都不是严格的方阵,读者还应掌握更为一般化的广义逆矩阵(也称为伪逆)概念。然而,即使有了广义逆矩阵,当自变量x的个数(既所选特征的个数)大于样本个数n时,最小二乘法仍会失效。
这时,梯度下降法是一个不错的求解策略。
- 机器学习
众所周知,感知机(Perceptron)是支持向量机与神经网络等机器学习方法的基础。对于分类问题,其基本学习策略是寻找一条分类直线(高维数据时为超平面): ( w × x + b ) \left ( w\times x+b \right ) (w×x+b),最小化误分类点到该分类直线(超平面)之间的距离之和:
min w , b − 1 ∥ w ∥ ∑ x i ∈ M y i ( w × x i + b ) \min _ { w , b } - \frac { 1 } { \| w \| } \sum _ { x _ { i } \in M } y _ { i } \left( w \times x _ { i } + b \right) w,bmin−∥w∥1xi∈M∑yi(w×xi+b)
忽略 1 ∥ w ∥ \frac{1}{\left \| w \right \|} ∥w∥1后,便得到感知机的损失函数:
min w , b L ( w , b ) = − ∑ x i ∈ M y i ( w × x i + b ) \min _ { w , b } L ( w , b ) = - \sum _ { x _ { i } \in M } y _ { i } \left( w \times x _ { i } + b \right) w,bminL(w,b)=−xi∈M∑yi(w×xi+b)
上式中M为误分类点的集合,自变量x与分类标签y均由数据给出,w与b为分类直线(超平面)中的待估参数。
显然最小化该损失函数也是一个无约束最优化问题,可以用梯度下降法进行求解。
看过上面几个例子,我们将其归纳为一般的问题进行描述:首先,找到一个连续可微的函数作为待优化的函数,利用梯度下降法进行参数迭代估计,使可微函数在估计的参数处最优值达到最小。
2.概念理解
- 微分
我们所要优化的函数必须是一个连续可微的函数,可微,既可微分,意思是在函数的任意定义域上导数存在。如果导数存在且是连续函数,则原函数是连续可微的。在中学时我们便知道,函数的导数(近似于函数的微分)可以有以下两种理解:
- 函数在某点切线的斜率即为函数在该点处导数值。
- 函数在某点的导数值反应函数在该处的变化率,导数值越大,原函数函数值变化越快。
以上两个解释可以让我们对梯度下降法理解得更直观形象,下面我们一起来看几个连续可微函数求微分的例子:
- d ( x 2 ) d x = 2 x \frac { d \left( x ^ { 2 } \right) } { d x } = 2 x dxd(x2)=2x
- d ( 5 − θ ) 2 d θ = − 2 ( 5 − θ ) \frac { d ( 5 - \theta ) ^ { 2 } } { d \theta } = - 2 ( 5 - \theta ) dθd(5−θ)2=−2(5−θ)
上面这两个例子高中生都会,下面看看多元连续可微函数求微分的例子:
- ∂ ∂ x ( x 2 y 2 ) = 2 x y 2 \frac { \partial } { \partial x } \left( x ^ { 2 } y ^ { 2 } \right) = 2 x y ^ { 2 } ∂x∂(x2y2)=2xy2
- ∂ ∂ y ( − 2 y 5 + z 2 ) = − 10 y 4 \frac { \partial } { \partial y } \left( - 2 y ^ { 5 } + z ^ { 2 } \right) = - 10 y ^ { 4 } ∂y∂(−2y5+z2)=−10y4
- ∂ ∂ θ 2 [ 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) ] = − 2 \frac { \partial } { \partial \theta _ { 2 } } \left[ 0.55 - \left( 5 \theta _ { 1 } + 2 \theta _ { 2 } - 12 \theta _ { 3 } \right) \right] = - 2 ∂θ2∂[0.55−(5θ1+2θ2−12θ3)]=−2
- 梯度
学习梯度下降算法,不知道什么是梯度可不行!
以二元函数 z = f ( x , y ) z=f\left ( x,y \right ) z=f(x,y)为例,假设其对每个变量都具有连续的一阶偏导数 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z和 ∂ z ∂ y \frac{\partial z}{\partial y} ∂y∂z,则这两个偏导数构成的向量 [ ∂ z ∂ x , ∂ z ∂ y ] \left [ \frac{\partial z}{\partial x},\frac{\partial z}{\partial y} \right ] [∂x∂z,∂y∂z]即为该二元函数的梯度向量,一般记作 ▽ f ( x , y ) \triangledown f\left ( x,y \right ) ▽f(x,y),其中 ▽ \triangledown ▽读作“Nabla”。根据这个概念,我们来看几个多元函数求梯度的例子:
-
J ( Θ ) = 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) J\left ( \Theta \right )=0.55-\left ( 5\theta _{1} +2\theta _{2}-12\theta _{3}\right ) J(Θ)=0.55−(5θ1+2θ2−12θ3)
▽ J ( Θ ) = [ ∂ J ∂ θ 1 , ∂ J ∂ θ 2 , ∂ J ∂ θ 3 ] = [ − 5 , − 2 , 12 ] \triangledown J\left ( \Theta \right )= \left [ \frac{\partial J}{\partial \theta _{1}},\frac{\partial J}{\partial \theta _{2}},\frac{\partial J}{\partial \theta _{3}} \right ]\\ = \left [ -5,-2,12 \right ] ▽J(Θ)=[∂θ1∂J,∂θ2∂J,∂θ3∂J]=[−5,−2,12]
-
J ( Θ ) = 1 2 [ 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) ] 2 J\left ( \Theta \right )=\frac{1}{2}\left [ 0.55-\left ( 5\theta _{1}+2\theta _{2}-12\theta _{3} \right ) \right ]^{2} J(Θ)=21[0.55−(5θ1+2θ2−12θ3)]2
▽ J ( Θ ) = [ ∂ J ∂ θ 1 , ∂ J ∂ θ 2 , ∂ J ∂ θ 3 ] = [ − 5 ( 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) ) , − 2 ( 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) ) , 12 ( 0.55 − ( 5 θ 1 + 2 θ 2 − 12 θ 3 ) ) ] \triangledown J\left ( \Theta \right )= \left [ \frac{\partial J}{\partial \theta _{1}},\frac{\partial J}{\partial \theta _{2}},\frac{\partial J}{\partial \theta _{3}} \right ]\\ = \left [ -5\left ( 0.55-\left ( 5\theta _{1}+2\theta _{2}-12\theta _{3} \right ) \right ),-2\left ( 0.55-\left ( 5\theta _{1}+2\theta _{2}-12\theta _{3} \right ) \right ),12\left ( 0.55-\left ( 5\theta _{1}+2\theta _{2}-12\theta _{3}\right ) \right ) \right ] ▽J(Θ)=[∂θ1∂J,∂θ2∂J,∂θ3∂J]=[−5(0.55−(5θ1+2θ2−12θ3)),−2(0.55−(5θ1+2θ2−12θ3)),12(0.55−(5θ1+2θ2−12θ3))]
注意,上面两个例子中的 Θ = ( θ 1 , θ 2 , θ 3 ) \Theta =\left ( \theta _{1}, \theta _{2}, \theta _{3} \right ) Θ=(θ1,θ2,θ3)。
在一元函数中,梯度其实就是微分,既函数的变化率,而在多元函数中,梯度变为了向量,同样表示函数变化的方向,从几何意义来讲,梯度的方向表示的是函数增加最快的方向,这正是我们下山要找的“最陡峭的方向”的反方向!因此后面要讲到的迭代公式中,梯度前面的符号为“-”,代表梯度方向的反方向。在多元函数中,梯度向量的模(一般指二模)表示函数变化率,同样的,模数值越大,变化率越快。
- 学习率 α \alpha α
学习率也被称为迭代的步长,优化函数的梯度一般是不断变化的(梯度的方向随梯度的变化而变化),因此需要一个适当的学习率约束着每次下降的距离不会太多也不会太少。读者可参考上面讲过的下山例子中下山距离的讲解,此处不再赘述。
3.梯度下降算法原理
在清楚我们要解决的问题并明白梯度的概念后,下面开始正式介绍梯度下降算法。根据计算梯度时所用数据量不同,可以分为三种基本方法:批量梯度下降法(Batch Gradient Descent, BGD)、小批量梯度下降法(Mini-batch Gradient Descent, MBGD)以及随机梯度下降法(Stochastic Gradient Descent, SGD)。
这里首先给出梯度下降法的一般求解框架:
给定待优化连续可微函数 J ( Θ ) J\left ( \Theta \right ) J(Θ)、学习率 α \alpha α以及一组初始值 Θ 0 = ( θ 01 , θ 02 , ⋯ , θ 0 l , ) \Theta _{0}=\left ( \theta _{01}, \theta _{02}, \cdots,\theta _{0l}, \right ) Θ0=(θ01,θ02,⋯,θ0l,)
计算待优化函数梯度: ▽ J ( Θ 0 ) \triangledown J\left ( \Theta _{0} \right ) ▽J(Θ0)
更新迭代公式: Θ 0 + 1 = Θ 0 − α ▽ J ( Θ 0 ) \Theta ^{0+1}=\Theta _{0}-\alpha \triangledown J\left ( \Theta_{0} \right ) Θ0+1=Θ0−α▽J(Θ0)
计算 Θ 0 + 1 \Theta ^{0+1} Θ0+1处函数梯度 ▽ J ( Θ 0 + 1 ) \triangledown J\left ( \Theta _{0+1} \right ) ▽J(Θ0+1)
计算梯度向量的模来判断算法是否收敛: ∥ ▽ J ( Θ ) ∥ ⩽ ε \left \| \triangledown J\left ( \Theta \right ) \right \| \leqslant \varepsilon ∥▽J(Θ)∥⩽ε
若收敛,算法停止,否则根据迭代公式继续迭代
注意:以上叙述只是给出了一个梯度下降算法的一般框架,实际应用过程中,还应灵活变换该框架使其符合实际。例如,可以更改迭代公式(例如学习率前面的符号,因为如果求max的话,梯度的方向即为函数值上升最快的方向,此时符号应为“+”),还可以用其他指标(例如KL散度、迭代前后优化函数值的变化程度等)判断算法的收敛性等等。
在下面的介绍中,为了便于理解,我们均假设待优化函数为二模损失函数:
J ( Θ ) = 1 2 n ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) 2 J\left ( \Theta \right )=\frac{1}{2n}\sum_{i=1}^{n}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )^{2} J(Θ)=2n1i=1∑n(hθ(x(i))−y(i))2
其中,n为样本个数,也可以理解为参与计算的样本个数; 1 2 \frac{1}{2} 21是一个常数,为了求偏导数时与平方抵消方便,不影响计算复杂度与计算结果; x ( i ) x^{\left ( i \right )} x(i)与 y ( i ) y^{\left ( i \right )} y(i)为第i个样本; h θ ( x ( i ) ) = θ 0 + θ 1 x 1 ( i ) + ⋯ + θ n x n ( i ) h_{\theta } \left ( x^{\left ( i \right )}\right )=\theta _{0}+\theta _{1}x_{1}^{\left ( i \right )}+\cdots +\theta _{n}x_{n}^{\left ( i \right )} hθ(x(i))=θ0+θ1x1(i)+⋯+θnxn(i),x的下标表示第i个样本的各个分量。
- 批量梯度下降法
批量梯度下降法在计算优化函数的梯度时利用全部样本数据:
梯度计算公式: ∂ J ( Θ ) ∂ θ j = 1 n ∑ i = 1 n ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J\left ( \Theta \right ) }{\partial \theta _{j}}=\frac{1}{n}\sum_{i=1}^{n}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x_{j}^{\left (i \right )} ∂θj∂J(Θ)=n1∑i=1n(hθ(x(i))−y(i))xj(i)
这里可以清楚地看到,批量梯度下降法计算梯度时,使用全部样本数据,分别计算梯度后除以样本个数(取平均)作为一次迭代使用的梯度向量。
迭代公式为: θ = θ − η ⋅ ▽ θ J ( θ ) \theta =\theta -\eta \cdot \triangledown _{\theta }J\left ( \theta \right ) θ=θ−η⋅▽θJ(θ)
伪代码如下:
for i in range(max_iters):
grad = evaluate_gradient(loss_functiion, data, initial_params)
params = params - learning_rate * grad
- 随机梯度下降法
随机梯度下降法在计算优化函数的梯度时利用随机选择的一个样本数据:
梯度计算公式: ∂ J ( Θ ) ∂ θ j = ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J\left ( \Theta \right ) }{\partial \theta _{j}}=\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x_{j}^{\left (i \right )} ∂θj∂J(Θ)=(hθ(x(i))−y(i))xj(i)
SGD只是用一个样本数据参与梯度计算,因此省略了求和以及求平均的过程,降低了计算复杂度,因此提升了计算速度。
迭代公式为: θ = θ − η ⋅ ▽ θ J ( θ ; x ( i ) ; y ( i ) ) \theta =\theta -\eta \cdot \triangledown _{\theta }J\left ( \theta;x^{\left ( i \right )} ;y^{\left ( i \right )} \right ) θ=θ−η⋅▽θJ(θ;x(i);y(i))
伪代码如下:
for i in range(max_iters):
np.random.shuffle(data)
for sample in data:
grad = evaluate_gradient(loss_functiion, sample, initial_params)
params = params - learning_rate * grad
- 小批量梯度下降法
小批量梯度下降法在计算优化函数的梯度时利用随机选择的一部分样本数据:
梯度计算公式: ∂ J ( Θ ) ∂ θ j = 1 k ∑ i i + k ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J\left ( \Theta \right ) }{\partial \theta _{j}}=\frac{1}{k}\sum_{i}^{i+k}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x_{j}^{\left (i \right )} ∂θj∂J(Θ)=k1∑ii+k(hθ(x(i))−y(i))xj(i)
小批量梯度下降法使用一部份样本数据(上式中为k个)参与计算,既降低了计算复杂度,又保证了解的收敛性。
迭代公式为: θ = θ − η ⋅ ▽ θ J ( θ ; x ( i : i + k ) ; y ( i : i + k ) ) \theta =\theta -\eta \cdot \triangledown _{\theta }J\left ( \theta;x^{\left ( i:i+k \right )} ;y^{\left ( i:i+k \right )} \right ) θ=θ−η⋅▽θJ(θ;x(i:i+k);y(i:i+k))
伪代码如下(假设每次选取50个样本参与计算):
for i in range(max_iters):
np.random.shuffle(data)
for batch in get batches(data, batch_size=50):
grad = evaluate_gradient(loss_functiion, batch, initial_params)
params = params - learning_rate * grad
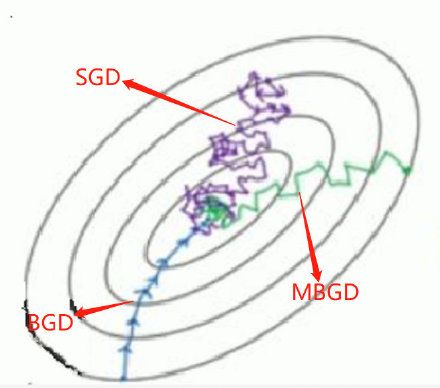
三种方法优缺点对比:
| BGD(批量) | SGD(随机) | MBGD(小批量) | |
|---|---|---|---|
| 优点 | 非凸函数可保证收敛至全局最优解 | 计算速度快 | 计算速度快,收敛稳定 |
| 缺点 | 计算速度缓慢,不允许新样本中途进入 | 计算结果不易收敛,可能会陷入局部最优解中 | — |
其实,已经有研究发现,当逐渐减小SGD方法使用的学习率时,可以保证SGD解的收敛性,但不一定保证收敛至全局最优解。此外,许多深度学习方法所使用的求解算法都是基于MBGD的,该方法一个算不上缺点的“缺点”就是需要找到合适的参与梯度计算的样本规模,对于超过2000个样本的较大数据集而言,参与计算的样本规模建议值为 2 6 2^{6} 26至 2 8 2^{8} 28。下面这张图形象的显示了三种梯度下降算法的收敛过程:
- 简单实例
求:
函数 f ( x ) = f ( x 1 , x 2 ) = 1 3 x 1 2 + 1 2 x 2 2 f\left ( x \right )=f\left ( x_{1},x_{2}\right )=\frac{1}{3}x_{1}^{2}+\frac{1}{2}x_{2}^{2} f(x)=f(x1,x2)=31x12+21x22的极小值点。
解:
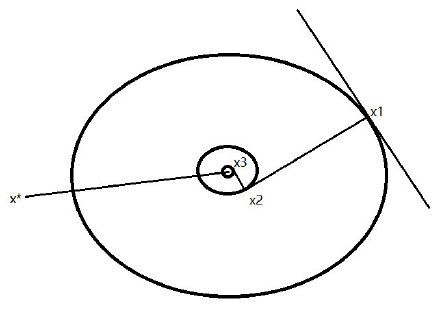
设初始点为 x 1 = ( x 1 ( 1 ) , x 2 ( 1 ) ) ⊤ = ( 3 , 2 ) ⊤ x_{1}=\left ( x_{1}^{\left ( 1 \right )},x_{2}^{\left ( 1 \right )} \right )^{\top }=\left ( 3,2 \right )^{\top } x1=(x1(1),x2(1))⊤=(3,2)⊤,学习率设为 λ \lambda λ。
初始点处梯度为 g 1 = g ( x 1 ) = ( 2 , 2 ) ⊤ ≠ 0 g _ { 1 } = g \left( x _ { 1 } \right) = ( 2,2 ) ^ { \top } \neq 0 g1=g(x1)=(2,2)⊤̸=0,因此更新迭代公式带入原函数中,得:
f ( x 2 ) = f ( x 1 − λ g 1 ) = 10 3 λ 2 − 8 λ + 5 f\left ( x_{2} \right )=f\left ( x_{1}-\lambda g_{1} \right )=\frac{10}{3}\lambda ^{2}-8\lambda +5 f(x2)=f(x1−λg1)=310λ2−8λ+5,此时 λ 1 ∗ = 6 5 \lambda _{1}^{*}=\frac{6}{5} λ1∗=56为函数极小点,因此:
x 2 = x 1 − λ 1 ∗ g 1 = ( 3 5 , − 2 5 ) ⊤ x_{2}=x_{1}-\lambda _{1}^{*}g_{1}=\left ( \frac{3}{5},-\frac{2}{5} \right )^{\top } x2=x1−λ1∗g1=(53,−52)⊤,一次迭代结束。
再将 x 2 x_{2} x2作为初始点,重复上面的迭代步骤,得到: x 3 = ( 3 5 2 , 2 5 2 ) ⊤ x_{3}=\left ( \frac{3}{5^{2}},\frac{2}{5^{2}} \right )^{\top } x3=(523,522)⊤。
根据规律显然可知, x k = ( 3 5 k − 1 , ( − 1 ) k − 1 2 5 k − 1 ) ⊤ x_{k}=\left ( \frac{3}{5^{k-1}},\left ( -1 \right )^{k-1}\frac{2}{5^{k-1}} \right )^{\top } xk=(5k−13,(−1)k−15k−12)⊤。
容易看出,本例中目标函数 f ( x ) f\left ( x \right ) f(x)是三维空间中的椭圆抛物面,其投影至二维空间上的等高线是一簇椭圆(如下图所示)。 f ( x ) f\left ( x \right ) f(x)的极小点就是这簇椭圆的中心 x ∗ = ( 0 , 0 ) ⊤ x^{*}=\left ( 0,0 \right )^{\top } x∗=(0,0)⊤。我们求得的迭代公式 { x k } \left \{ x_{k} \right \} {xk}是逐渐趋近于 x ∗ x^{*} x∗的,算法正确有效。
至此,梯度下降法的原理部分就结束了。作者感觉本篇应该是全网最清楚明白的讲解之一了,为了了解了大家的疑问,在动笔前参看了许多优秀的博文以及留言,最终形成此文。希望能对热爱学习的你有所帮助!
后续还有机器学习算法:梯度下降法的代码篇(Python & R)以及拓展篇,敬请期待!
4.参考文献
- 邓乃扬 等 . 无约束最优化计算方法[M]. 1982.
- Ruder S . An overview of gradient descent optimization algorithms[J]. 2016.
- Udacity . Gradient Descent - Problem of Hiking Down a Mountain
- @六尺帐篷 . 深入浅出–梯度下降法及其实现. 简书