二叉搜索树
文章目录
- 98. 验证二叉搜索树
- 669. 修剪二叉搜索树
- 230. 二叉搜索树中第K小的元素 (中等)
- 538. 把二叉搜索树转换为累加树 (简单)
- 235. 二叉搜索树的最近公共祖先
- 108. 将有序数组转换为二叉搜索树
- 109. 有序链表转换二叉搜索树 (*)
- 653. 两数之和 IV - 输入 BST (*)
- 530. 二叉搜索树的最小绝对差
- 501. 二叉搜索树中的众数 (简单*)
按照中序遍历非递减<=> 二叉搜索树
通常不出现重复元素。
98. 验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
题解:
- 思路一
中序遍历二叉树,看序列是否递增。
访问当前节点时,看当前节点值是否大于前一次访问的节点值。
注意的点,
- 前一次访问的节点
min初始化为:double min = - Double.MAX_VALUE; - 边界情况:空树为二叉搜索树;一个节点的树为二叉搜索树
- 中序遍历迭代版:root 存的是入栈节点,top 存的是访问即出栈节点。两者不可用同一个遍历来存,不然会陷入无限循环:同一节点入栈和出栈。
JAVA代码:
class Solution {
public boolean isValidBST(TreeNode root) {
if (root == null) return true;
if (root.left == null && root.right==null) return true;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
double min = - Double.MAX_VALUE; //min初始化为最小的整数
while (!stack.isEmpty()){
if (root.left!=null){//左侧链入栈
root = root.left;
stack.push(root);
}
else{//访问左侧链最后一个节点,并转向右子树
TreeNode top = stack.pop(); //访问
//比较当前节点与前一次访问节点
if (top.val <= min)
return false;
min = top.val;
//转向右子树
if (top.right!= null){
root = top.right;
stack.push(root);
}
}
}
return true;
}
}
- 思路二
基于边界的递归
在遍历树的同时保留结点的上界与下界,在比较时不仅比较子结点的值,也要与上下界比较。
class Solution {
public boolean helper(TreeNode node, Integer lower, Integer upper) {
if (node == null) return true;
int val = node.val;
if (lower != null && val <= lower) return false;
if (upper != null && val >= upper) return false;
if (! helper(node.right, val, upper)) return false;
if (! helper(node.left, lower, val)) return false;
return true;
}
public boolean isValidBST(TreeNode root) {
return helper(root, null, null);
}
}
669. 修剪二叉搜索树
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
示例 1:
输入:
1
/ \
0 2
L = 1
R = 2
输出:
1
\
2
示例 2:
输入:
3
/ \
0 4
\
2
/
1
L = 1
R = 3
输出:
3
/
2
/
1
题解:
DFS先序遍历,从根开始修剪
- 若当前结点值
- 若当前结点值>L,保留左子树,继续修剪左子树
- 否则,当前结点保留,修剪左子树和右子树。
class Solution {
public TreeNode trimBST(TreeNode root, int L, int R) {
if (root == null) return null;
if (root.val < L) return trimBST(root.right, L, R);
if (root.val > R) return trimBST(root.left, L, R);
root.left = trimBST(root.left, L, R);
root.right = trimBST(root.right, L, R);
return root;
}
}
时间复杂度O(n)
空间复杂度O(h)
230. 二叉搜索树中第K小的元素 (中等)
给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。
说明:
你可以假设 k 总是有效的,1 ≤ k ≤ 二叉搜索树元素个数。
示例 1:
输入: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
输出: 1
示例 2:
输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/ \
3 6
/ \
2 4
/
1
输出: 3
进阶:
如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化 kthSmallest 函数?
题解:
1. 思路一: DFS递归
二叉搜索树通常没有相同的结点值,因此中序遍历单调递增。
用一个全局变量记录访问的结点个数,中序遍历时,访问到的第k个元素即为第k小的结点。
//中序遍历有序
class Solution {
int res = 0;
int i = 0;
public int kthSmallest(TreeNode root, int k) {
help(root,k);
return res;
}
public void help(TreeNode root, int k){
if (root == null) return;
help(root.left,k);
i++;
if (i == k){
res = root.val;
}
help(root.right,k);
}
}
时间复杂度:O(n)
空间复杂度:O(n)
- 思路二
Morris
可参考:https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by–48/
538. 把二叉搜索树转换为累加树 (简单)
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。
例如:
输入: 原始二叉搜索树:
5
/ \
2 13
输出: 转换为累加树:
18
/ \
20 13
注意:本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同。
题解:
DFS: 右根左递归遍历
由于访问过的结点值都比当前结点值大
- 因此用一个全局变量记录访问过的结点之和
- 当前结点值为加上访问过的结点的之和即可
class Solution {
int add = 0;
public TreeNode convertBST(TreeNode root) {
if (root == null) return root;
convertBST(root.right);
root.val += add;
add = root.val;
convertBST(root.left);
return root;
}
}
时间复杂度O(n)
空间复杂度O(h)
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
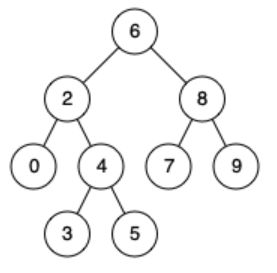
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
题解:
1. 思路一:DFS递归
根据二叉搜索树的性质:
- 任一节点的值大于左子树任何节点,且小于右子树任何节点。
因此最近公共祖先有三种情况:
- 若当前节点小于p和q,那么最近公共祖先在该节点右子树上
- 若当前节点大于p和q,那么最近公共祖先在该节点左子树上
- 以上情况均不满足:当前节点左边有p右边有q,或者
当前节点做百年则该节点为最近公共祖先
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root==null) return null;
if (root.val< q.val && root.val < p.val){
return lowestCommonAncestor(root.right, p, q);
}
if (root.val>p.val && root.val>q.val)
return lowestCommonAncestor(root.left, p, q);
return root;
}
}
时间复杂度:O(n)
空间复杂度:O(h)
2.思路二:指针迭代
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root!=null){
if (root.val < p.val && root.val < q.val){
if (root.right!=null) root = root.right;
}
else if (root.val > p.val && root.val > q.val){
if (root.left != null) root = root.left;
}
else{
return root;
}
}
return null;
}
}
时间复杂度O(n)
空间复杂度O(1)
108. 将有序数组转换为二叉搜索树
- 先序递归
- 每次寻找数组中位数作为根节点
- 中位数左边的数构造左子树
- 中位数右边的数构造右子树
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return help(nums, 0, nums.length-1);
}
public TreeNode help(int[] nums, int L, int R){
if (L > R) return null;
int mid = L - ((L-R)>>1);
TreeNode root = new TreeNode(nums[mid]);
root.left = help(nums, L, mid-1);
root.right = help(nums, mid+1, R);
return root;
}
}
时间复杂度O(n)
空间复杂度O(logn)
109. 有序链表转换二叉搜索树 (*)
有序链表无法像数组根据下标寻找中间数。
可用一个快指针,一个慢指针来找链表中间数。
- 每次找链表中间数,即快指针所指节点作为根节点
- 链表从中间切断,前一部分构造左子树,后一部分构造右子树
class Solution {
public TreeNode sortedListToBST(ListNode head) {
return help(head);
}
public TreeNode help(ListNode head){
ListNode preP1 = null;
ListNode p1 = head; //慢指针
ListNode p2 = head; //快指针
if (head == null) return null;
while(p2!=null && p2.next!=null){
preP1 = p1;
p1 = p1.next;
p2 = p2.next.next;
}
TreeNode root = new TreeNode(p1.val);
if (preP1!=null) preP1.next = null; //从中间断开
if (p1 == head) return root; //只有一个节点:中间节点即head节点,直接返回root
root.left = help(head);
root.right = help(p1.next);
return root;
}
}
时间复杂度: n/2 + 2*(n/4) + 4*(n/8) = O(nlogn)
空间复杂度:O(logn)
-
思路二: 递归+转数组
时间复杂度:O(n)
空间复杂度:O(n) -
中序递归 (*)
//中序递归
class Solution {
ListNode node;
public TreeNode sortedListToBST(ListNode head) {
node = head;
int n = 0;
while(head!=null){
n++;
head = head.next;
}
return help(0, n-1);
}
public TreeNode help(int L, int R){
if (L>R) return null;
int mid = L - ((L-R)>>1);
TreeNode left = help(L,mid-1);
TreeNode root = new TreeNode(node.val);
node = node.next;
root.left = left;
root.right = help(mid+1, R);
return root;
}
}
时间复杂度O(n)
空间复杂度O(logn)
653. 两数之和 IV - 输入 BST (*)
给定一个二叉搜索树和一个目标结果,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
案例 1:
输入:
5
/ \
3 6
/ \ \
2 4 7
Target = 9
输出: True
案例 2:
输入:
5
/ \
3 6
/ \ \
2 4 7
Target = 28
输出: False
1. 思路一:使用HashSet (*)
HashSet中存放访问过的节点值。
遍历搜索树,每次看Set中是否存在 k-root.val, 若存在,即可返回True; 否则将当前节点值加入Set中。
注意的地方:整个过程最多只访问每个节点一次:每判断一次将当前节点值放入Set; 而不用先遍历一遍搜索树将整个节点加入Set中后再遍历一次。
class Solution {
public boolean findTarget(TreeNode root, int k) {
Set<Integer> set = new HashSet<>();
return help(root, k, set);
}
//寻找差值节点
public boolean help(TreeNode root, int k, Set set){
if (root == null) return false;
if (set.contains(k-root.val)) return true;
set.add(root.val);
return help(root.left, k, set) || help(root.right, k, set);
}
}
时间复杂度:O(n)
空间复杂度:O(n)
2. 思路二:使用 BFS 和 HashSet
Set与方法一相同,不同的是使用广度优先遍历二叉树。
3. 思路三:使用BST的性质 (*)
BST: 中序遍历结果按升序排序
用一个List保存中序遍历结果。用两个指针L和R分别指向List的头和尾.
- 若L和R位置元素之和等于k, 则返回True;
- 若小于k, L向右移动一位(和不够大,右移增大两数之和)
- 若小于k, R向左移动一位
class Solution {
public boolean findTarget(TreeNode root, int k) {
List<Integer> list = new ArrayList<>();
help(root, list);
int L=0, R = list.size()-1;
while (L<R){
if (list.get(L) + list.get(R) == k)
return true;
else if (list.get(L) + list.get(R) < k)
L++;
else
R--;
}
return false;
}
//中序遍历
public void help(TreeNode root, List list){
if (root == null) return;
help(root.left, list);
list.add(root.val);
help(root.right, list);
}
}
时间复杂度O(n)
空间复杂度O(n)
530. 二叉搜索树的最小绝对差
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
示例:
输入:
1
\
3
/
2
输出:
1
解释:
最小绝对差为 1,其中 2 和 1 的差的绝对值为 1(或者 2 和 3)。
- 思路一: 中序遍历 + List
用一个List保存中序遍历结果:升序
升序序列最小绝对值之差必然是相邻两个元素产生的。
因此只需遍历List,计算相邻两个元素的差,并记录最小差即可。
class Solution {
public int getMinimumDifference(TreeNode root) {
List<Integer> list = new ArrayList<>();
help(root, list); //list元素升序排列
int min = list.get(1) - list.get(0);
for (int i = 2; i< list.size(); i++){
min = list.get(i) - list.get(i-1)<min? list.get(i) - list.get(i-1):min;
}
return min;
}
//中序遍历二叉树,节点存放在List中
public void help(TreeNode root, List list){
if (root == null) return;
help(root.left, list);
list.add(root.val);
help(root.right, list);
}
}
时间复杂度O(n)
空间复杂度O(n)
- 思路二:中序遍历 + 双指针
BST中序遍历是升序序列,因此最小绝对值之差由两个中序遍历过程相邻两个节点产生。
用两个指针指向两个相邻节点。
class Solution {
TreeNode pre = null;
int min = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
help(root);
return min;
}
//中序遍历二叉树,计算相邻两个节点的差
public void help(TreeNode root){
if (root == null) return;
help(root.left);
if (pre!=null)
min = root.val - pre.val < min? root.val - pre.val: min;
pre = root;
help(root.right);
}
}
时间复杂度O(n)
空间复杂度O(h)
501. 二叉搜索树中的众数 (简单*)
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
结点左子树中所含结点的值小于等于当前结点的值
结点右子树中所含结点的值大于等于当前结点的值
左子树和右子树都是二叉搜索树
例如:
给定 BST [1,null,2,2],
1
\
2
/
2
返回[2].
**提示:**如果众数超过1个,不需考虑输出顺序
**进阶:**你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
题解:
- 中序遍历 + list
中序遍历相同元素必定相邻
list存放当前遍历过的结点中个数最多的。
root:当前节点
pre: root前一个结点
MaxCount: 访问过结点个数最多结点的个数
count: 与当前结点值相同的结点个数
当count 与MaxCount相同时,将当前结点值加入list
当count大于MaxCount时,清空list,并将当前结点值加入list,更新MaxCount为count
class Solution {
List<Integer> list = new LinkedList<Integer>();
int count = 1;
int MaxCount = 0;
TreeNode pre = null;
public int[] findMode(TreeNode root) {
// if (!root) return list;
inOrder(root);
int size = list.size();
int[] res = new int[size];
for (int i = 0; i<size; i++){
res[i] = list.get(i);
}
return res;
}
//中序遍历
void inOrder(TreeNode root){
if (root == null) return;
inOrder(root.left);
if (pre!=null)
count = (root.val == pre.val) ? count + 1 : 1;
if (count == MaxCount)
list.add(root.val);
else if (count > MaxCount){
list.clear();
list.add(root.val);
MaxCount = count;
}
pre = root;
inOrder(root.right);
}
}
时间复杂度 O(n)
空间复杂度O(h) + 最糟糕情况O(n): 每个值都只有一个