计算机视觉学习12：图像内容分类(KNN算法和稠密SIFT(Dense-SIFT)以及手势识别）

KNN算法(K近邻算法）

一、KNN算法概述

kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

二、KNN算法介绍

最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来，当测试对象的属性和某个训练对象的属性完全匹配时，便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢，其次就是存在一个测试对象同时与多个训练对象匹配，导致一个训练对象被分到了多个类的问题，基于这些问题呢，就产生了KNN。 KNN是通过测量不同特征值之间的距离进行分类。它的的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 下面通过一个简单的例子说明一下：如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

由此也说明了KNN算法的结果很大程度取决于K的选择。
在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：
同时，KNN通过依据k个对象中占优的类别进行决策，而不是单一的对象类别决策。这两点就是KNN算法的优势。
接下来对KNN算法的思想总结一下：就是在训练集中数据和标签已知的情况下，输入测试数据，将测试数据的特征与训练集中对应的特征进行相互比较，找到训练集中与之最为相似的前K个数据，则该测试数据对应的类别就是K个数据中出现次数最多的那个分类，其算法的描述为：
1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的K个点；
4）确定前K个点所在类别的出现频率；
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

三、算法实现

KNN算法的python实现
给定训练样本集和对应的标记列表，定义一个类并用训练集数据初始化非常简单，每次想对某些东西进行分类时，用KNN方法，我们就没有必要存储并将训练数据作为参数来传递。用一个字典来存储邻近标记，我们便可以用文本字符串或数字来表示标记。在这个例子中，我们用欧式距离（L２）进行度量。
KNN.py

from numpy import * 

class KnnClassifier(object):
    
    def __init__(self,labels,samples):
        """ 使用训练数据初始化分类器 """
        
        self.labels = labels
        self.samples = samples
    
    def classify(self,point,k=3):
        """ 在训练数据上采用K近邻分类，并返回标记. """
        
        # 计算所有训练数据点的距离
        dist = array([L2dist(point,s) for s in self.samples])
        
        #对它们进行排序
        ndx = dist.argsort()
        
        #用字典存储K近邻
        votes = {}
        for i in range(k):
            label = self.labels[ndx[i]]
            votes.setdefault(label,0)
            votes[label] += 1
            
        return max(votes, key=lambda x: votes.get(x))


def L2dist(p1,p2):
    return sqrt( sum( (p1-p2)**2) )

def L1dist(v1,v2):
    return sum(abs(v1-v2))

四、实验部分

1、创建两个不同的二维点集，每个点集有两类，用Pickle模块用来保存创建的数据

# -*- coding: utf-8 -*-
from numpy.random import randn
import pickle
from pylab import *

# 创建二维样本数据
n = 200
# 两个正态分布数据集
class_1 = 0.6 * randn(n, 2)
class_2 = 1.2 * randn(n, 2) + array([5, 1])
labels = hstack((ones(n), -ones(n)))
# 用Pickle模块保存
# with open('points_normal.pkl', 'w') as f:
with open('points_normal_test.pkl', 'wb') as f:
    pickle.dump(class_1, f)
    pickle.dump(class_2, f)
    pickle.dump(labels, f)
# 正态分布，并使数据成环绕状分布
print("save OK!")
class_1 = 0.6 * randn(n, 2)
r = 0.8 * randn(n, 1) + 5
angle = 2 * pi * randn(n, 1)
class_2 = hstack((r * cos(angle), r * sin(angle)))
labels = hstack((ones(n), -ones(n)))
# 用Pickle保存
# with open('points_ring.pkl', 'w') as f:
with open('points_ring_test.pkl', 'wb') as f:
    pickle.dump(class_1, f)
    pickle.dump(class_2, f)
    pickle.dump(labels, f)

print("save OK!")

2、

# -*- coding: utf-8 -*-
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

pklist=['points_normal.pkl','points_ring.pkl']

figure()

# l用Pickle载入二维数据点
for i, pklfile in enumerate(pklist):
    with open(pklfile, 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)
    # 用Pickle模块载入测试数据集
    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

    model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
    # 在测试集的第一个数据点上进行测试
    print (model.classify(class_1[0]))

    # 定义绘图函数
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # 绘制分类边界
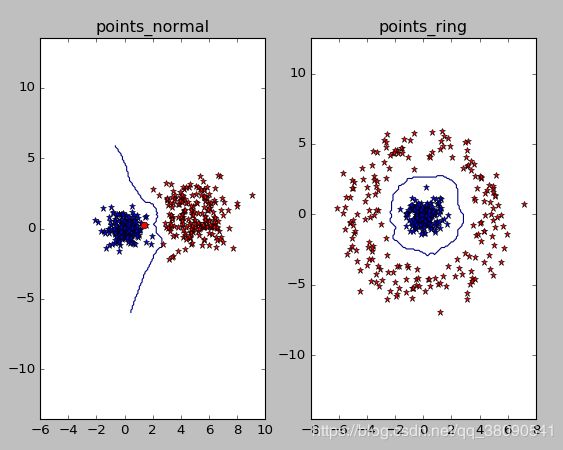
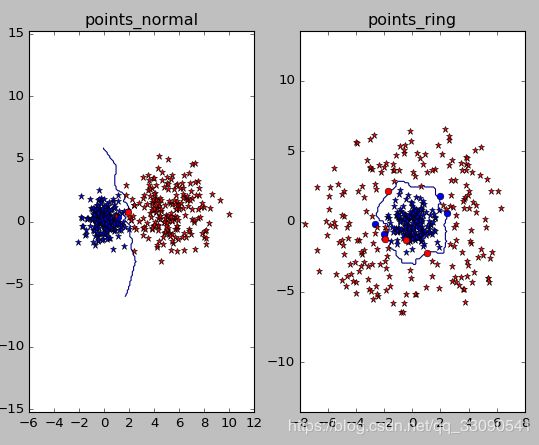
    subplot(1,2,i+1)
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
    savefig("test1.png")
show()

实验结果

稠密SIFT算法（Dense-SIFT)

一、原理

传统的SIFT算法即Sparse SIFT，不能很好地表征不同类之间的特征差异，达不到所需的分类要求。而Dense SIFT算法，是一种对输入图像进行分块处理，再进行SIFT运算的特征提取过程。Dense SIFT根据可调的参数大小，来适当满足不同分类任务下对图像的特征表征能力。
该算法首先将表达目标的矩形区域分成相同大小的矩形块,计算每一个小块的SIFT特征,再对各个小块的稠密SIFT特征在中心位置进行采样,建模目标的表达.然后度量两个图像区域的不相似性,先计算两个区域对应小块的Bhattacharyya距离,再对各距离加权求和作为两个区域间的距离.因为目标所在区域靠近边缘的部分可能受到背景像素的影响,而区域的内部则更一致,所以越靠近区域中心权函数的值越大.最后提出了能适应目标尺度变化的跟踪算法。

二、实验部分

1、稠密SIFT(Dense-sift)实现

from PIL import Image
from numpy import *
import os

from PCV.localdescriptors import sift

def process_image_dsift(imagename,resultname,size=20,steps=10,force_orientation=False,resize=None):
    """ 用密集采样的SIFT描述子处理一幅图像，并将结果保存在一个文件。可选的输入：特征的大小size，位置之间的步长steps,是否强迫计算描述子的方位force_orientation(False表示所有的方位都是朝上的)，用于调整图像大小的元组."""

    im = Image.open(imagename).convert('L')
    if resize!=None:
        im = im.resize(resize)
    m,n = im.size
    
    if imagename[-3:] != 'pgm':
        #create a pgm file
        im.save('tmp.pgm')
        imagename = 'tmp.pgm'

    # 创建帧，并保存到临时文件
    scale = size/3.0
    x,y = meshgrid(range(steps,m,steps),range(steps,n,steps))
    xx,yy = x.flatten(),y.flatten()
    frame = array([xx,yy,scale*ones(xx.shape[0]),zeros(xx.shape[0])])
    savetxt('tmp.frame',frame.T,fmt='%03.3f')
    
    path = os.path.abspath(os.path.join(os.path.dirname("__file__"),os.path.pardir))
    #path = path + "\\python3-ch08\\win32vlfeat\\sift.exe "
    if force_orientation:
        cmmd = str("sift " + imagename + " --output=" + resultname + " --read-frames=tmp.frame --orientations")
        #cmmd = str(path + imagename + " --output=" + resultname + " --read-frames=tmp.frame --orientations")
        print ('processed1', imagename, 'to', resultname)
    else:
        cmmd = str("sift " + imagename + " --output=" + resultname + " --read-frames=tmp.frame")
        #cmmd = str(path + imagename + " --output=" + resultname +" --read-frames=tmp.frame")
        print('processed2', imagename, 'to', resultname)
    os.system(cmmd)

2、计算稠密SIFT描述子，并可视化它们的位置
（本实验采用的依旧是集美大学图片）

# -*- coding: utf-8 -*-
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

#dsift.process_image_dsift('gesture/empire.jpg','empire.dsift',90,40,True)
dsift.process_image_dsift('ch3.jpg','ch3.dsift',90,40,True)
l,d = sift.read_features_from_file('ch3.dsift')
im = array(Image.open('ch3.jpg'))
sift.plot_features(im,l,True)
title('dense SIFT')
show()

手势识别

一、实验代码

# -*- coding: utf-8 -*-
from PCV.localdescriptors import dsift
import os
from PCV.localdescriptors import sift
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

imlist = imtools.get_imlist('test')
for filename in imlist:
    featfile = filename[:-3]+'dsift'
    dsift.process_image_dsift(filename,featfile,1,1)

def get_imagelist(path):
    """    Returns a list of filenames for
        all jpg images in a directory. """

    return [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.jpg')]

def read_gesture_features_labels(path):
    # create list of all files ending in .dsift
    featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
    # read the features
    features = []
    for featfile in featlist:
        l,d = sift.read_features_from_file(featfile)
        features.append(d.flatten())
    features = array(features)
    # create labels
    labels = [featfile.split('/')[-1][0] for featfile in featlist]
    return features,array(labels)

def print_confusion(res,labels,classnames):
    n = len(classnames)
    # confusion matrix
    class_ind = dict([(classnames[i],i) for i in range(n)])
    confuse = zeros((n,n))
    for i in range(len(test_labels)):
        confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
    print ('Confusion matrix for')
    print (classnames)
    print (confuse)

filelist_train = get_imagelist('train')
filelist_test = get_imagelist('test')
imlist=filelist_train+filelist_test

# process images at fixed size (50,50)
for filename in imlist:
    featfile = filename[:-3]+'dsift'
    dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))

features,labels = read_gesture_features_labels('train')
test_features,test_labels = read_gesture_features_labels('test')
classnames = unique(labels)

# test kNN
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
# accuracy
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print ('Accuracy:', acc)

print_confusion(res,test_labels,classnames)

# -*- coding: utf-8 -*-
import os
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

imlist=['train/A-uniform02.jpg','train/B-uniform02.jpg',
        'train/O-uniform01.jpg','train/Four-uniform01.jpg',
        'train/Three-uniform02.jpg','train/Point-uniform01.jpg']
        #'train/C-uniform01.jpg']
#'train/Four-uniform01.jpg','train/O-uniform01.jpg','train/Three-uniform01.jpg','train/B-uniform01.jpg']

figure()
for i, im in enumerate(imlist):
    print (im)
    dsift.process_image_dsift(im,im[:-3]+'dsift',90,40,True)
    l,d = sift.read_features_from_file(im[:-3]+'dsift')
    dirpath, filename=os.path.split(im)
    im = array(Image.open(im))
    #显示手势含义title
    titlename=filename[:-14]
    subplot(2,3,i+1)
    sift.plot_features(im,l,True)
    title(titlename)
show()

二、实验结果