数据结构-队列

队列

先入先出的数据结构(FIFO)

在FIFO数据结构中，将首先处理添加到队列中的第一个元素。插入(insert)操作称为入队(enqueue),新元素始终被添加在队列的末尾。删除(delete)操作被称为出队(dequeue)。你只能移除第一个元素。

顺序队列-实现

为了实现队列，我们可以使用动态数组和指向队列头部的索引。
如上所述，队列应支持两种操作：入队和出队。入队会向队列追加一个新元素，而出队会删除第一个元素。 所以我们需要一个索引来指出起点

class MyQueue {
    // 存储元素
    private List data;         
    // 指示起始位置的指针
    private int p_start;            
    public MyQueue() {
        data = new ArrayList();
        p_start = 0;
    }

    /** 向队列中插入一个元素，如果操作成功则返回true*/
    public boolean enQueue(int x) {
        data.add(x);
        return true;
    };    
     /** 向队列中删除一个元素，如果操作成功则返回true*/
    public boolean deQueue() {
        if (isEmpty() == true) {
            return false;
        }
        p_start++;
        return true;
    }
    /** 从队列中获取前端项. */
    public int Front() {
        return data.get(p_start);
    }
    /** 检查队列是否为空. */
    public boolean isEmpty() {
        return p_start >= data.size();
    }     
};

public class Main {
    public static void main(String[] args) {
        MyQueue q = new MyQueue();
        q.enQueue(5);
        q.enQueue(3);
        if (q.isEmpty() == false) {
            System.out.println(q.Front());
        }
        q.deQueue();
        if (q.isEmpty() == false) {
            System.out.println(q.Front());
        }
        q.deQueue();
        if (q.isEmpty() == false) {
            System.out.println(q.Front());
        }
    }
}

队列进阶-循环队列

队列顺序存储的不足

队列元素的入列就是在队尾追加一个元素，不需要移动任何元素，因此时间复杂度为O(1)

队列元素的出列是在队头，即下标为0的位置，那就意味着，队列中的所有元素都得向前移动，以保证队列里的队头(也就是下标为0的位置)不为空，此时的时间复杂度为O(n)。

如果不去限制队列的元素必须存储在数组的前n个单元这一条件，出队的性能就会大大增加。也就是说，队头不需要一定在下标为0的位置。

为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以可引入两个指针，front指针指向队头元素，rear指针指向队尾元素的下一个位置，这样当front等于rear时，此队列不是还剩一个元素，而是空队列。
假设一个长度为5的数组，初始状态，空队列如下左图所示，front与rear指针均指向下标为0的位置。然后入队a1,a2,a3,a4,front指针依然指向下标为0的位置，rear指针指向下标为4的位置。

出队a1,a2,则front指针指向下标为2的位置，rear不变。然后在入队a5，此时front指针不变，rear指针会移动到数组之外，这种现象叫作假溢出。

假设一个队列的总个数不超过5个，但目前如果接着入队的话，因数组末尾元素已经被占用，再向后加，就会产生数组越界的错误，可实际上我们的队列在下标为0和1的地方还是空闲的

循环队列-解决假溢出问题

解决假溢出的办法就是后面满了，就再从头开始，也就是头尾相接循环。队列的这种头尾相接的顺序存储结构称为循环队列。
如果出现数组越界，rear指针改为指向下标为0的位置，继续存储数据

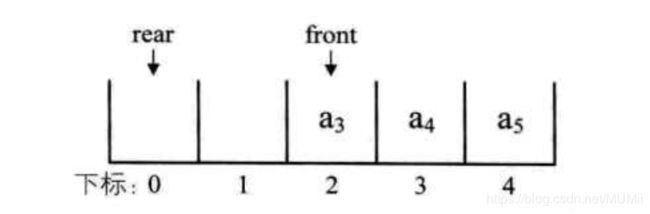
接着在入队a6,将其放置于下标为0处，rear指针指向下标为1处。若在入队a7，则rear指针就与front指针重合，同时指向下标为2的位置。但是该种方式无法判断队列究竟是空的还是满的，因为front等于rear时，队列既可是空队列也可是满队列。

让我们来继续优化
当队列为空时，条件就是front = rear，当队列为满时，我们修改其条件，保留一个元素空间。也就是说队列满时，数组中还有一个空闲单元。

此时判断队列是否满的条件是：(rear+1)%QueueSize == front

QueueSize：表示队列的最大尺寸

循环队列-实现

class MyCircularQueue {
    private int[] data;
    private int head;
    private int tail;
    private int size;

    /** 构造器，设置队列长度为 k. */
    public MyCircularQueue(int k) {
        data = new int[k];
        head = -1;
        tail = -1;
        size = k;
    }
    
    /** 向循环队列插入一个元素。如果成功插入则返回真 */
    public boolean enQueue(int value) {
        if (isFull() == true) {
            return false;
        }
        if (isEmpty() == true) {
            head = 0;
        }
        tail = (tail + 1) % size;
        data[tail] = value;
        return true;
    }
    
    /** 从循环队列中删除一个元素。如果成功删除则返回真 */
    public boolean deQueue() {
        if (isEmpty() == true) {
            return false;
        }
        if (head == tail) {
            head = -1;
            tail = -1;
            return true;
        }
        head = (head + 1) % size;
        return true;
    }
    
    /** 从队首获取元素。如果队列为空，返回 -1 */
    public int Front() {
        if (isEmpty() == true) {
            return -1;
        }
        return data[head];
    }
    
    /** 获取队尾元素。如果队列为空，返回 -1 */
    public int Rear() {
        if (isEmpty() == true) {
            return -1;
        }
        return data[tail];
    }
    
    /** 检查循环队列是否为空. */
    public boolean isEmpty() {
        return head == -1;
    }
    
    /** 检查循环队列是否已满 */
    public boolean isFull() {
        return ((tail + 1) % size) == head;
    }
}