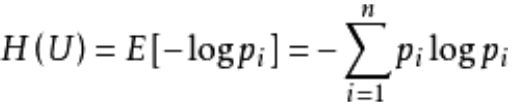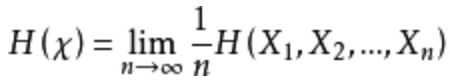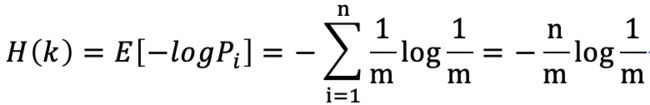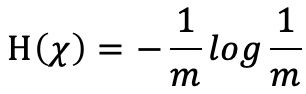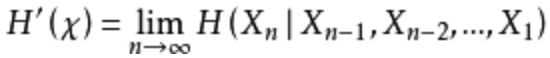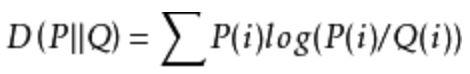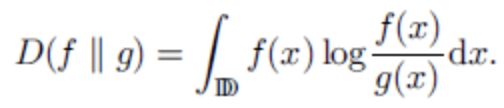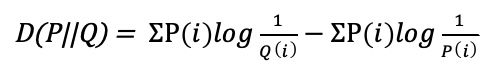直观理解-信息熵&KL Divergence
信息熵
简介
任何信息都存在冗余,冗余大小与信息中每个符号的出现概率或者说不确定性有关。
信息熵用于解决对信息的量化度量问题,描述信源的不确定度。
香农第一次用数学语言阐明了概率与信息冗余度的关系。
基本内容
通常一个信源发送出什么符号是不确定的,衡量它可以根据其出现的概率来度量,概率大,出现的机会多,不确定性小;反之不确定性大。
不确定函数f应该
1、满足概率P的减函数。
2、两个独立符号所产生的不确定性应该等于各个不确定性之和,即f(P1,P2)=f(P1)+f(P2),这称为可加性。
同时满足这两个条件的函数f为对数函数。
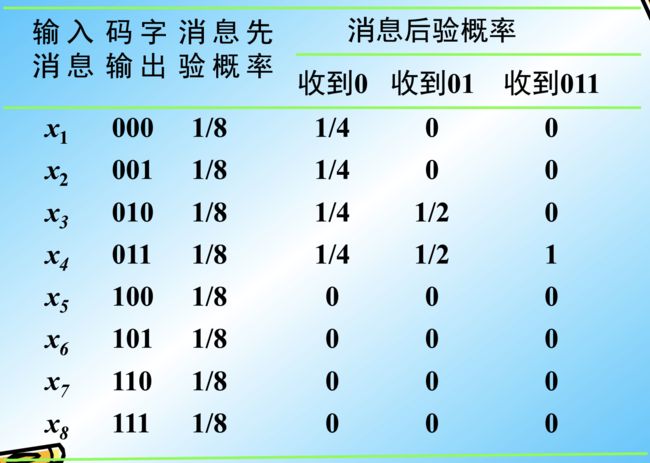
eg.
由例子:
-
当未接收到任何信息时,信息的不确定度为log(1/(1/8))=3bits
-
当收到一个0时候,已经确定了一个bit,那么只有可能在x1~x4中,此时不确定性变为log(1/(1/4))=2bits。3-2正好为1bit。
-
依此类推,当收到011时,已经可以完全确定为x4,此时信息的不确定性为0。
所以获取信息就是我们消除不确定性。
在信源中,考虑的不是某一个单一符号发生的不确定性,而是考虑这个信源所有可能发生情况的平均不确定性。若信源符号有n种取值:U1,U2,U3……Un对应概率为:P1,P2,P3……Pn,各种符号出现彼此独立。这时信源的平均不确定性应当为单个符号不确定性的统计平均值E,则称为信息熵。
式中对数一般取2为底,单位为比特。但是也可以取其他对数为底,采用其他相应的单位,他们之间可用换底公式转换。
举例
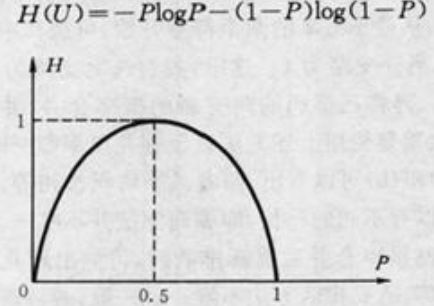
最简单的单符号信源仅取0和1两个元素,即二元信源,其概率为P和Q=1-P,该信源的熵如图。
直观理解
好比海上有有一座灯塔,但是灯塔上的灯由于电线接触不良,亮和不亮是随机的。如果灯塔上有人,就可以在灯灭的时候及时点亮。此时灯塔就是一个信源,会出现下面的情况:
1、灯塔一直亮就代表塔上有人,灯塔一直不亮就代表塔上没人。此时信息是确认的,所以信息熵为0.
2、灯塔亮的频率高,说明有人的概率高。灯塔不亮的概率高,说明没人的概率高。当亮和不亮的几率刚好都为0.5的时候,我们最难猜测灯塔上有没有人。所以此时灯塔这个信源传出的信息的不确定信是最高的,信息熵为1.
这与热力学的熵是一致的,熵越大,越混乱,不确定程度越高。
离散信源的信息熵特性
1、非负性:即收到一个信源符号所获的的信息量应为正值。
2、对称性:对称与P=0.5
3、确定性:H(1,0)=0,即P=0或P=1是确定状态,所得信息量为0
4、极值性:因H(U)是P上的上凸函数,且一阶导在P=0.5时等于0.所以P=0.5时H(U)最大。
(对于连续信源,香农给出了形式上类似于离散信源的连续熵Hc(U),虽然连续熵仍具有可加性,但不具有非负性。但是在表达信源差距时,仍然具有非负性,这与力学中势能的定义相仿。)
信息熵参考文献
熵率
引入背景
如果给定长度为n的随机变量序列,那么这个序列的熵随n如何增长?所以引入熵率。
定义
当以下极限存在时候,随机过程{Xi}的熵率定义为:
eg
打字机可以等可能输出m个字母,由此打字机产生长度为n的序列k。
则序列k的信息熵
熵率为
该打字机的熵率为常数(即单个字符的信息熵),所以没增加一个字符,他的熵增加量是恒定的。
(归纳:对于独立同分布的随机变量,熵率就等于其单个变量的熵)
条件熵
但是,对一些独立但非同分布的随机变量序列,因为对每个元素的熵是不相等的,所以极限不存在。
此时可以定义熵率的一个相关量(如果下列极限存在):
H和H‘这两个量反映了熵率概念的两个不同方面。第一个量指的是n个随机变量的每字符熵,第二个变量指在已知前面n-1随机变量的情况下最后一个随机变量的条件熵。
重要定理
定理1
对于平稳随机过程,H与H’均存在极限,并且相等。
定理2
对于平稳随机过程,H‘存在极限,并随n递减。
谱熵(Spectral Entropy)
简介
描述了功率谱和熵率之间的关系
实例
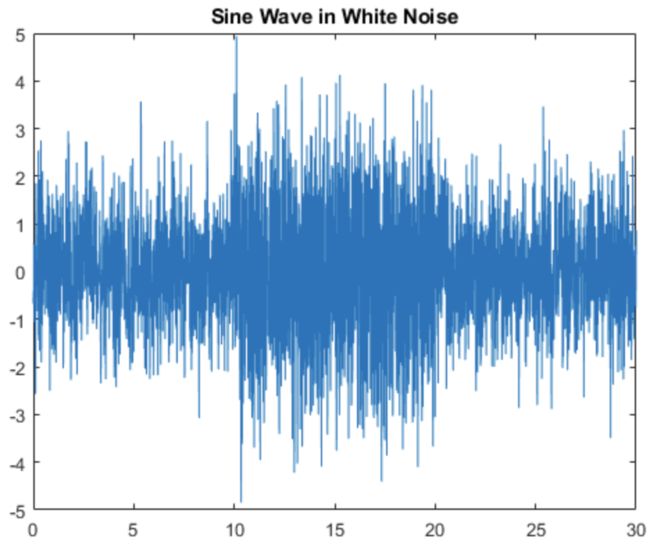
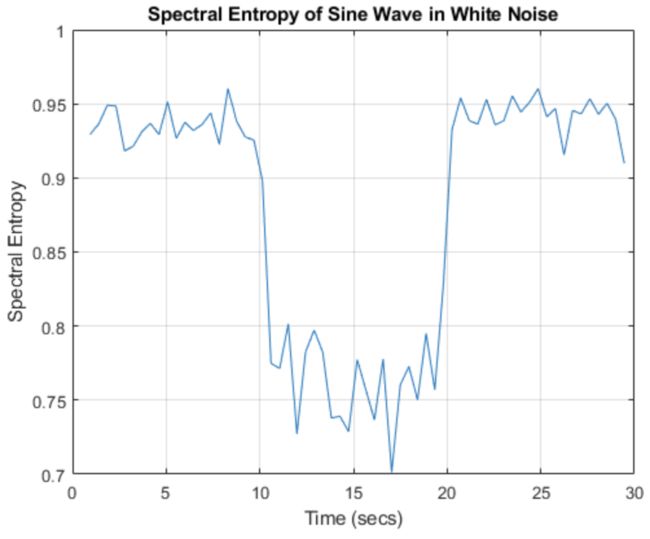
实例1 在白噪声中检测正弦信号
这是一段白噪声,在中间加入了正弦信号。
对这段信号计算spectral entropy(谱熵),可以容易发现,中间含有正弦信号的区域,谱熵明显降低。这是因为正弦信号的信息的出现使得这段信号的不确定性下降了。
参考资料:matlab求熵函数官方文档
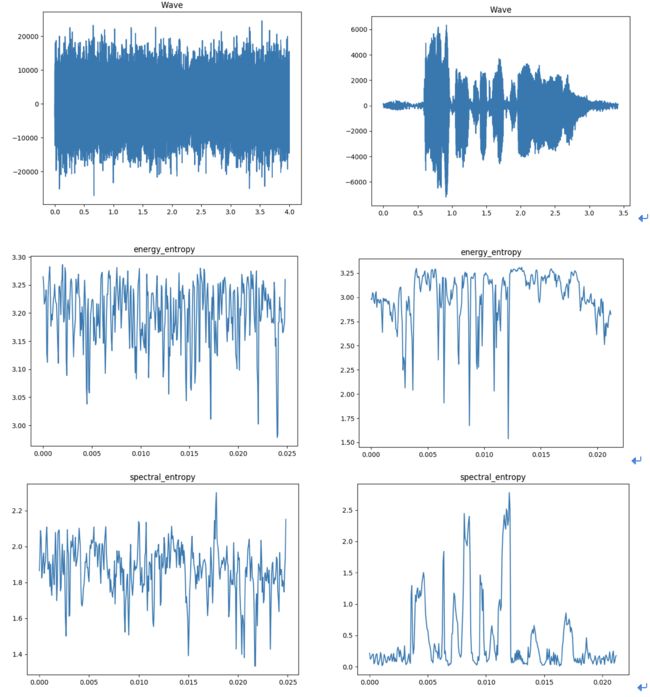
实例2 噪声与语音信号的能量熵与谱熵
可以看出,噪声的信息不确定性要明显高于语音信号。
KL Divergence
简介
在概率论或者信息论中,KL散度又称为相对熵(relative entropy),是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着它是非对称的,即D(P||Q) ≠ D(Q||P)。
特别的,在信息论中,D(P||Q)表示当用概率分布Q来拟合真实分布P时,会产生的信息损耗,其中P是真实分布,Q表示P的拟合分布。
有人将KL散度称为KL距离,但实际上,KL散度不满足距离的概念:
1、KL散度是非对称的。
2、KL散度不满足三角不等式。
定义式
离散型
连续型
性质
KLD是非负的。
直观理解
将离散型KLD公式展开
可以看到这是两个离散型的信息熵,而第一项用Q拟合P会产生信息损失,那么信息的不确定性会增大,从而信息熵就会增大。所以第一项大于第二项。整体KLD为正。
所以当KLD越小,信息不确定性(损失)越小,说明拟合程度越高。
参考资料-KL散度