2020 CCPC Wannafly Winter Camp Day1 (部分题解)
7-1 1A. 期望逆序对
按中点从小到大排序之后n^2求一遍答案。 赛后补题 by zx
#include
#include
#include
#include
#include
#define LL long long
#define PII pair
#define PLL pair
#define inf 0x3f3f3f3f
#define test freopen("in.txt","r",stdin);freopen("out.txt","w",stdout);
using namespace std;
int n;
const int maxn=5e3+5,mod=998244353;
PII p[maxn];
bool cmp(PII lhs,PII rhs)
{
return lhs.first+lhs.secondp[r].second)
{
tmp+=1ll*(p[l].second-p[r].second)*len2;
tmp+=1ll*(len2)*(len2-1)/2;
}
else if(p[l].second>p[r].first)
{
int len1=(p[l].second-p[l].first+1);
if(p[l].first>p[r].first) tmp+=1ll*len1*(p[l].first-p[r].first)+1ll*len1*(len1-1)/2;
else tmp+=1ll*(p[l].second-p[r].first)*(p[l].second-p[r].first+1)/2;
}
tmp%=mod;
res.first=tmp;
return res;
}
LL qpow(LL a,LL b)
{
LL res=1;
while(b)
{
if(b&1) res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
int main()
{
//test
scanf("%d",&n);
for(int i=0;i 7-2 1B. 密码学
签到题,solved by cyh
#include7-3 1C. 染色图
先康康 g ( n , k ) g(n,k) g(n,k)等于什么:n个图有k个颜色的话,给每个点分配颜色之后,每两个不同颜色的点连边,直觉告诉我们(事实上也可以证明),分配的越平均,边的数量越多。
令 x = ⌊ n k ⌋ , y = n m o d k = n − k x x = \lfloor\frac{n}{k}\rfloor, y=n\ mod\ k=n-kx x=⌊kn⌋,y=n mod k=n−kx
那么有 y y y种颜色染了 x + 1 x+1 x+1个点, k − y k-y k−y种颜色染了 x x x个点。
这种分配下可以连的边数为: ( k − y ) ∗ x ∗ ( n − x ) + k ∗ ( x + 1 ) ∗ ( n − x + 1 ) (k-y)*x*(n-x)+k*(x+1)*(n-x+1) (k−y)∗x∗(n−x)+k∗(x+1)∗(n−x+1)
化出来之后可得 g ( n , k ) = n 2 − n − 2 n x + ( x 2 + x ) k g(n,k)=n^2-n-2nx+(x^2+x)k g(n,k)=n2−n−2nx+(x2+x)k
因为要求 ∑ k = l r g ( n , k ) \sum_{k=l}^{r}g(n,k) ∑k=lrg(n,k),可以用分块处理这个式子。
值得注意的是不能用求两次前缀和然后相减的套路,会T。原因应该是因为除法分块前面密后面疏,而从1开始求前缀和每次都会从密到疏,而只扫一遍就很快,不过极端数据情况下他们的差别应该不会太大,而这道题这两种方法时间差距接近1000倍……
solve by wwb
#include
#define ll long long
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
using namespace std;
const ll mod = 998244353;
ll n;
ll sol(ll x, ll y){
ll l = x, r;
ll ans = 0;
while(l <= y){
r = n/(n/l);
if(r > y) r = y;
ll t = n/l;
//cout<<"t:"<>T;
ll l, r;
ll inv2 = (mod+1)/2;
//scanf("%lld%lld%lld", &n, &l, &r);
while(T--){
scanf("%lld%lld%lld", &n, &l, &r);
//ll ans = sol(r) - sol(l-1);
ll ans = sol(l, r);
ans %= mod;
ans = (ans + mod)%mod;
ans = (ans*inv2)%mod;
printf("%lld\n", ans);
// cout< 7-5 1E. 树与路径
很容易求得某个结点为根的时候的答案,所以想到用一个已经求得答案的点去更新其他点。先定一个结点为树根求得答案。然后在这颗有根树上:
考虑有一条路径是这样的,它们的lca为点f:
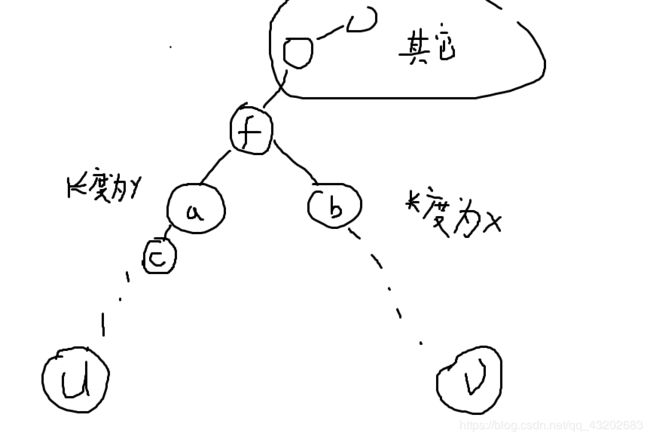
那么u->v这条路径给f贡献的答案为 A f = x y A_f=xy Af=xy
给结点a贡献的答案为 A a = ( y − 1 ) ( x + 1 ) A_a=(y-1)(x+1) Aa=(y−1)(x+1)
给结点c贡献的答案为 A c = ( y − 2 ) ( x + 2 ) A_c=(y-2)(x+2) Ac=(y−2)(x+2)
…
可以发现,
A a − A f = y − x − 1 , A c − A a = y − x − 3 , . . . A_a-A_f=y-x-1,\\A_c-A_a=y-x-3,\\... Aa−Af=y−x−1,Ac−Aa=y−x−3,...
从u到f这条路径上的点(不包括f),节点的答案和该节点父节点的答案的差值构成一个以-2为公差的等差数列。
每次来一个查询,我们在对应的两条链上加上相应的等差数列,最后每个节点和父节点的差值就都知道了。然后从根节点dfs一遍就可以得到所有答案。
这里使用树链剖分+线段树来维护链上的等差数列,复杂度 O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)。
因为在最后才查询,所以也可以差分来简单快捷的实现链上加等差数列的操作。
#include
#define ll long long
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
using namespace std;
const int maxn = 5e5 + 50;
int dfn[maxn], id[maxn], son[maxn], sz[maxn], fa[maxn], top[maxn], dep[maxn], idx = 0;
vector g[maxn];
int n, m;
ll ans[maxn];
void dfs1(int u, int f){
sz[u] = 1; fa[u] = f; dep[u] = dep[f] + 1;
for(int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
if(v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if(sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u){
dfn[++idx] = u; id[u] = idx;
if(son[u]) top[son[u]] = top[u], dfs2(son[u]);
for(int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
if(v == fa[u] || v == son[u]) continue;
top[v] = v;
dfs2(v);
}
}
int lca(int u, int v){
while(top[u] != top[v]){
if(dep[top[u]] > dep[top[v]]) swap(u, v);
v = fa[top[v]];
}if(dep[u] > dep[v]) swap(u, v);
return u;
}
void init(){
scanf("%d%d", &n, &m);
for(int i = 1; i< n; ++i){
int u, v;
scanf("%d%d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}
dfs1(1, 0); top[1] = 1; dfs2(1);
}
ll lza[maxn<<2], lzb[maxn<<2];
void down(int rt, int l, int r){
lza[rt<<1] += lza[rt];
lzb[rt<<1] += lzb[rt];
lza[rt<<1|1] += lza[rt] + (mid-l+1)*lzb[rt];
lzb[rt<<1|1] += lzb[rt];
lza[rt] = lzb[rt] = 0;
}
void update(int rt, int l, int r, int L, int R, ll a, ll b){
// cout<<"L:"< mid) {
if(L <= mid) update(rson, L, R, a+(mid-max(L, l)+1)*b, b);//attention
else update(rson, L, R, a, b);
}
return;
}
void Q(int u, int v){
int p = lca(u, v);
ll y = dep[u] - dep[p];
ll x = dep[v] - dep[p];
// cout<<"y:"< 7-6 1F. 乘法
想到去二分,这道题在思路上就基本上完成了大半了。然后在二分答案之后分类讨论正负号之后求比判定值小(或者大,取决于写法)的乘积的个数。我这里是分类讨论之后枚举a中的数字然后二分找对应的b中的位置来求的。0处理起来细节繁琐,wa六发之后重构把0单独考虑就好写一些了。
solved by wwb
#include
#define ll long long
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pb push_back
using namespace std;
ll n, m, k;
vector a1, b1, a2, b2;
ll za, zb;
ll check(ll x){
ll res = 0;
if(x < 0){
for(int i = 0; i < a1.size(); ++i){
ll t = x/a1[i];
if(t*a1[i] != x) t++;
res += b2.end() - lower_bound(b2.begin(), b2.end(), t);
}
for(int i = 0; i < b1.size(); ++i){
ll t = x/b1[i];
if(t*b1[i] != x) t++;
res += a2.end() - lower_bound(a2.begin(), a2.end(), t);
}
}else{
res += (ll)a1.size()*(ll)b2.size() + (ll)a2.size()*(ll)b1.size();
res += zb*(ll)(a1.size() + a2.size()) + za*(ll)(b1.size() + b2.size()) + za*zb;
if(x == 0) return res;
for(int i = 0; i < a1.size(); ++i){
ll t = x/a1[i];
if(t == 0) continue;
res += b1.end()-lower_bound(b1.begin(), b1.end(), t);
}
for(int i = 0; i < a2.size(); ++i){
ll t = x/a2[i];
if(t == 0) continue;
res += upper_bound(b2.begin(), b2.end(), t)-b2.begin();
}
}
return res;
}
int main()
{
//cout<<3/-5<>n>>m>>k;
k = n*m-k+1;
za = zb = 0;
for(int i = 0; i < n; ++i){
ll x; scanf("%lld", &x);
if(x < 0) a1.pb(x);
else if(x > 0) a2.pb(x);
else za++;
}
for(int i = 0; i < m; ++i){
ll x; scanf("%lld", &x);
if(x < 0) b1.pb(x);
else if(x > 0) b2.pb(x);
else zb++;
}
sort(a1.begin(), a1.end());
sort(a2.begin(), a2.end());
sort(b1.begin(), b1.end());
sort(b2.begin(), b2.end());
ll l = -1e13, r = 1e13;
ll ans;
while(l <= r){
if(check(mid) >= k) {
ans = mid;
r = mid-1;
}else l = mid+1;
}cout< 7-8 1H. 最大公约数
给n,k,要找一个y使得y与k的gcd与[1,n]内除k外所有数字不同。那么首先我们知道gcd(k,y)一定等于k,否则如果gcd(k,y)=x
import math
def isprime(n):
if n < 2:
return False
for i in range(2,int(math.sqrt(n))+1):
if n % i == 0:
return False
return True
T=int(input())
for t in range(1,T+1):
n,k=map(int,input().split(' '))
ans=k
i=2;
while i*k<=n :
if isprime(i):
ans=ans*i
i=i+1
print(ans)
7-9 1I. K小数查询
考虑分块,更新的时候整块更新,然后再暴力更新边缘的块。
每个块维护一个排好序的数组。
查询的时候二分答案,然后在每个完整块内用二分在排好序的数组上查询块内多少个数小于等于要check的值。不完整的块暴力处理。
这里分的块大小为 p = n l o g n p=\sqrt{nlogn} p=nlogn
查询复杂度 O ( n p l o g ( p ) + p ) O(\frac{n}{p}log(p)+p) O(pnlog(p)+p)
更新复杂度 O ( n p + p ∗ l o g p ) O(\frac{n}{p}+p*logp) O(pn+p∗logp)
赛后补题 by wwb
#include
#define lowbit(x) ((x)&(-(x)))
#define mid ((l+r)>>1)
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define pb push_back
using namespace std;
const int maxn = 8e4 + 50;
const int inf = 0x3f3f3f3f;
int p, u;
int n, m;
int a[maxn];
int lz[maxn];
int L[maxn], R[maxn];
vector v[10050];
int get_id(int pos){
return pos/p;
}
void update(int l, int r, int x){
int id = get_id(l);
if(L[id] < l){//第一块暴力拆解
v[id].clear();
for(int i = L[id]; i <= R[id]; ++i){
a[i] = min(a[i], lz[id]);
if(i >= l && i <= r){
a[i] = min(a[i], x);
}
v[id].pb(a[i]);
}
sort(v[id].begin(), v[id].end());
id++;
}
if(id >= u) return;
while(R[id] <= r && id < u){//中间的完整块
lz[id] = min(lz[id], x);
id++;
}
if(id >= u || L[id] > r) return;
v[id].clear();
for(int i = L[id]; i <= R[id]; ++i){
a[i] = min(a[i], lz[id]);
if(i >= l && i <= r){
a[i] = min(a[i], x);
}
v[id].pb(a[i]);
}
sort(v[id].begin(), v[id].end());
return;
}
int check(int lim, int l, int r){
int id = get_id(l);
int res = 0;
if(L[id] < l){
for(int i = l; i <= min(R[id], r); ++i){
a[i] = min(a[i], lz[id]);
if(a[i] <= lim) res++;
}
id++;
}
//cout<<"res:"<= u) return res;
while(R[id] <= r && id < u){//中间的完整块
if(lz[id] <= lim) res += (R[id]-L[id]+1);
else res += upper_bound(v[id].begin(), v[id].end(), lim) - v[id].begin();
id++;
}
//cout<<"res2:"<= u || L[id] > r) return res;
for(int i = L[id]; i <= r; ++i){
a[i] = min(a[i], lz[id]);
if(a[i] <= lim) res++;
}
//cout<<"res3:"<= k){
ans = mid;
r = mid-1;
}else l = mid+1;
}
return ans;
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 0; i < n; ++i) scanf("%d", &a[i]);
p = sqrt(n*log(n));
if(p > n) p = n;
u = (n-1)/p+1;// id < u
for(int id = 0; id < u; ++id) {
lz[id] = inf;
L[id] = id*p, R[id] = id*p+p-1;
if(id == u-1) R[id] = n-1;
for(int i = L[id]; i <= R[id]; ++i) v[id].pb(a[i]);
sort(v[id].begin(), v[id].end());
}
//cout<<"p:"<