Bit Fields
By AllEightUp | Published Apr 15 2013 09:42 PM in Game Programming
Peer Reviewed by (Josh Vega, Dragonsoulj, Michael Tanczos)
During a discussion on GameDev recently, I suggested someone use a bit field as a method to avoid having to deal with various masking and shift operations in a manual and potentially buggy manner. The suggestion was taken and then a snippet of the code was given; everything looked correct at first glance but in fact it was incorrect. In the process of updating my suggestion for the specific usage, I did a bit of Googling for something simple, only to find that the usage of bit fields and solid information on behavior is severely lacking. I hope to centralize some of the information and also give some examples of bit fields beyond the trivial examples I found in my searches.
The general definition of a bit field is the ability to access and manipulate multiple logical neighboring bits in memory in a clean and concise manner. While technically correct this leaves a lot to be desired and also does not supply a very good reason to ever use a bit field in order to simplify your code. Additionally, the C and C++ standards leave some wiggle room in the definitions so there is a small amount of per compiler information to be learned when using bit fields. The standard was left loose due to the fact that a primary usage of bit fields in C was to map between the language and underlying hardware control registers. This is beyond the scope here but in order for compilers to map to specific hardware, sometimes the rules of how bits were laid out needed to be tweaked from platform to platform. It is the same reason that an ‘int’ in C/C++ does not specify that it is 32 or 64 bits in length explicitly; int can be tweaked to the best fit for the CPU and architecture.
In order to avoid any bad assumptions, we are going to base all examples and explanations on the idea that the target platform is an Intel x86 instruction set CPU and the compiler is set up accordingly. So, given that clarification, our first example is the following:
What this example is doing is defining specific bits within the fundamental unsigned short to be presented to the programmer as named fields which can be accessed or modified. The ‘Count’ field is specified as being 8 bits wide and as such has a valid range of 0-255. The ‘Offset’ is 7 bits wide and of course ‘Inverted’ is 1 bit. Using the bit field is as simple as accessing members of a structure in a normal fashion:
Nothing particularly surprising, so what good does specifying this as a bit field do? For one thing, in this case: “sizeof( a )==2”. We have packed all three of the fields into a single unsigned short, so it is compressed. The same structure without the bit field specifications would be “sizeof( a )==6”, quite a savings. The benefit to the programmer is that because we know the limits of intended data, we can pack the data into a smaller space; this is often used in network transmissions, file storage and other areas where you want to minimize the size of data.
The example so far packs into a single unsigned short because the number of bits used in total is 16, which happens to match the number of bits within the fundamental type we specified: unsigned short. So, what happens when the specification bit count is more than 16? Let’s change the example to be:
Now the count of bits says we have 17. There are two primary side effects of this change, the first being that “sizeof( BitField )!=2”, it is instead now “sizeof( BitField )==4”. The compiler has added another unsigned short to the structure in order to contain all the bits we specified, so there are now 15 bits which are unused in this structure. The second side effect is that the ‘Origin’ field which replaced ‘Inverted’ is no longer where you may expect it in the binary data. Instead of splitting the 2 bits, both bits are placed in the new element added to the structure. This means that in the first 16 bit value the high bit is no longer used and that there are actually only 14 unused bits in the newly added element.
Given that the compiler avoids splitting fields over the fundamental type boundaries, what happens if you tried the following?
The compiler will likely give you a warning, if not an error, on the ‘: 17’ portion saying that the specified bit count exceeds the size of the underlying type. Normally this means that the field will end up being only 16 bits long and you are not getting the 17th bit allocated. So, if you attempt to use the entire 17 bits the top bit will be truncated.
What happens when you try to specify the type of single bit fields as a ‘bool’ in C++:
You will be in for an unpleasant surprise with this definition as the behavior in this case is compiler specific. The C++ standard supplies no rules to standardize the behavior here and as such we have an example of Visual Studio and GCC/Clang differences. I could find no documentation about Visual Studio's behavior here and can only write the observed result and the guessed rules which cause it. The size of this bit field is actually 12, Visual Studio seems to close the first int, open a bool type for the single bit then open another int for the last two fields. On the other hand, both GCC and Clang seem to be just fine with packing the bool into the int type and the size of the bit field remains 4 bytes.
Another variation of this, with a different result, could be the following:
If you report the size of this structure, you will get 4 bytes again on the three compilers. Visual Studio does not seem to care if the type is signed or unsigned in this case, it only cares that the fundamental type sizeof is the same.
To be safe, it is suggested not to mix the fundamental types or at least do some serious testing to guarantee the compiler behavior. This is not a compiler bug, the C++ standard does not specify anything of use in clarifying the behavior here, so it is open to interpretation.
A primary item which my searches failed to show initially was which fundamental types were allowed, most results just showed “unsigned” in examples. When the results were more specific, most of the documentation you find refers to the C99 standard which specifies that the fundamental types can be one of: _Byte, signed int and unsigned int. But what about the C++ standards? This actually took a little digging but the answer is that C++ greatly expanded the allowed types to be: any integral type or enumeration type. So, in C++, fundamental types such as ‘long long’ (64 bit integer on x86) can be used as the type.
The enumeration type is a bit beyond the intended scope but enumerations are considered to be a signed integer type unless you use C++11 class typing on the enumeration. How the compiler interprets mixing the enumeration into the bit field is implementation defined and as such you need to test your compiler behavior.
By these definitions the prior examples, in C99, would have been flagged as warnings or errors due to the use of unsigned short. Though, most compilers did support this and other variations.
Mapping the bit fields to their binary representations is a compiler specific item, so this section may need to be researched for your compiler. On most modern compilers though (MSVC, GNU and Clang targeting x86/x64 code as examples), the general rule is that the fields take bits from the fundamental type in the order you specify starting with the first field taking the lowest bits and continuing up till ending the bit field or moving to the next fundamental type. So, for instance, our original example will have the following binary representation:
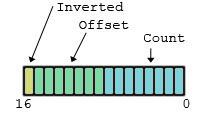
Packing bits tightly is only one of the abilities of a bit field. Additionally, you can insert padding and also control at what points a new fundamental type is allocated. We’ll use an example of mapping a hypothetical binary image format header to a bit field for easier manipulation and access. We’ll start with a textual description of the intentionally horrible image format header chunk:
Image Format:
Byte 0-1: Magic identifier: 0xf321
Byte 2: Version of format. Valid formats 0-5.
Byte 3: low nibble specifies x origin, high nibble specifies y origin. 0=top or left, 1=bottom or right.
Byte 4-7: Width of image. (Little endian.)
Byte 8-11: Height of image. (Little endian.)
Using bit fields we can define this as a structure which can be binary loaded and saved on a little endian CPU. The largest fundamental type described here is a 32 bit integer, so we want to end up with the width and height fields being represented as full integer values. Yet, at the same time we want to keep the bit counts we specify for the fields appropriate to the data ranges specified in the format. For instance, we know the valid formats are 0-5 so the first byte only has 3 bits of range involved. A naive method of mapping the description to a bit field would be to insert padding manually as follows:
Personally, I don’t like the unused ‘pad’ fields in my code, much less in an auto complete list if your editor supports such things. Additionally, I’d rather be explicit in expecting width to be in the next int as intended. So, we use unnamed fields in the definition to help out here:
This does exactly the same thing but now you don’t have to pepper the structure with ‘padx’ field names unless you have a specific purpose, in which case you could probably use a better name than ‘pad’. Say for instance, you expect to eventually allow more than 8 type versions and thus end up using some of the 5 padding bits. You could name the pad: “VersionReserved”. The name makes sense as it is reserved specifically for extension of the version field. But, assuming you don’t care about the bits for the time being, the unnamed field does the same job and doesn’t dirty up auto completions and such.
What exactly is the unnamed ‘0’ field though, 0 bits, huh? This is a special standards required behavior which tells the compiler to immediately allocate a new fundamental type for the next field to begin filling. While it is already implied that the 32 bit field will have to be placed in a new int since it won’t fit otherwise, this is an explicit hint for readability in this case.
So all the description is fine, but at this point you may be asking yourself, why would I ever bother with this? There are several cases where a bit field can be extremely valuable, either in simplification or in clearing up messy programming. I’ll give two examples in the following which could be used in today’s coding requirements.
Working with 16 bit colors can often cause a fair amount of headaches. You pass the color around as an uint16_t (unsigned short) but then need to manipulate the r, g and b components individually. Accessing the components individually involves masking out the relevant portions of the value and then shifting them into place for further work. So, for instance your color is probably packed as 5:6:5 such that there are 5 r and b bits and 6 g bits. Accessing the b bits is simple: “int b = color & 0x1f;”. Accessing r and g involve shifts, so for instance, to get the g you could use: “int g = (color>>5) & 0x3f;”. Replacing items in the colors is more complicated due to having to mask out the original value prior to inserting the new bits. Doing such accesses, even with helpers or macros is often error-prone so, in steps the bit field:
So the compiler does all the masking and shifting for you and makes the type a bit cleaner to use. Better yet, by using the bit field you are giving the compiler more opportunity to perform optimizations for you. Perhaps in a function where you extract the G twice, if you use shifts and masking yourself or a helper function, the compiler may not be able to recognize that they are both doing the same thing and eliminate one of the extractions. With the bit field, it is much more likely that the compiler will notice the duplication and remove it. But, considerably better, is that all the shifting and masking is handled by the compiler without hassles for the programmer.
Eventually, all programmers should probably understand the floating point format. But much as in the 16 bit color example, extracting and manipulating the bits in a float is both error-prone and often confusing. So, it is the bit field definition to the rescue once again:
Using this union allows you to write simplified code for several things. Duplicating some items in the standard libraries for instance, you could detect nan’s using the following code:
More important uses are beyond the scope of this article but an example would be implementing a tolerant equivalence check which scales with the magnitudes of the inputs. This is an important feature since the standard tolerance used by many programs is something like “abs( a-b ) > tolerance” which has to be specifically coded for the input data. If your values range from 1-100 the tolerances are likely in the ‘0.0001f’ range, but if your values are 0-1, the tolerance may need to be more like ‘0.00000001f’ to be useful. A more flexible tolerance is one which understands the binary representation and works as a percentage of difference instead of the fixed range used in the simple delta comparisons.
Hopefully you have a better understanding of bit fields, their possible uses and of course the idiosyncrasies of their implementations. Bringing all of the information into one place, with examples beyond the trivial, was the primary goal. Hopefully this short article will be a reasonable reference for people in the future.
15 April 2013: First pass clarification of binary representation.
13 April 2013: Initial release.
What Is A Bit Field
The general definition of a bit field is the ability to access and manipulate multiple logical neighboring bits in memory in a clean and concise manner. While technically correct this leaves a lot to be desired and also does not supply a very good reason to ever use a bit field in order to simplify your code. Additionally, the C and C++ standards leave some wiggle room in the definitions so there is a small amount of per compiler information to be learned when using bit fields. The standard was left loose due to the fact that a primary usage of bit fields in C was to map between the language and underlying hardware control registers. This is beyond the scope here but in order for compilers to map to specific hardware, sometimes the rules of how bits were laid out needed to be tweaked from platform to platform. It is the same reason that an ‘int’ in C/C++ does not specify that it is 32 or 64 bits in length explicitly; int can be tweaked to the best fit for the CPU and architecture.
In order to avoid any bad assumptions, we are going to base all examples and explanations on the idea that the target platform is an Intel x86 instruction set CPU and the compiler is set up accordingly. So, given that clarification, our first example is the following:
structBitField{ unsignedshort Count:8; unsignedshort Offset:7; unsignedshort Inverted:1;};
What this example is doing is defining specific bits within the fundamental unsigned short to be presented to the programmer as named fields which can be accessed or modified. The ‘Count’ field is specified as being 8 bits wide and as such has a valid range of 0-255. The ‘Offset’ is 7 bits wide and of course ‘Inverted’ is 1 bit. Using the bit field is as simple as accessing members of a structure in a normal fashion:
BitField a; a.Count=12; a.Offset=31; a.Inverted=0;
Nothing particularly surprising, so what good does specifying this as a bit field do? For one thing, in this case: “sizeof( a )==2”. We have packed all three of the fields into a single unsigned short, so it is compressed. The same structure without the bit field specifications would be “sizeof( a )==6”, quite a savings. The benefit to the programmer is that because we know the limits of intended data, we can pack the data into a smaller space; this is often used in network transmissions, file storage and other areas where you want to minimize the size of data.
Bit Field Overflow
The example so far packs into a single unsigned short because the number of bits used in total is 16, which happens to match the number of bits within the fundamental type we specified: unsigned short. So, what happens when the specification bit count is more than 16? Let’s change the example to be:
structBitField{ unsignedshort Count:8; unsignedshort Offset:7; unsignedshort Origin:2;};
Now the count of bits says we have 17. There are two primary side effects of this change, the first being that “sizeof( BitField )!=2”, it is instead now “sizeof( BitField )==4”. The compiler has added another unsigned short to the structure in order to contain all the bits we specified, so there are now 15 bits which are unused in this structure. The second side effect is that the ‘Origin’ field which replaced ‘Inverted’ is no longer where you may expect it in the binary data. Instead of splitting the 2 bits, both bits are placed in the new element added to the structure. This means that in the first 16 bit value the high bit is no longer used and that there are actually only 14 unused bits in the newly added element.
Given that the compiler avoids splitting fields over the fundamental type boundaries, what happens if you tried the following?
structBitField{ unsignedshort WhatsThis:17;};
The compiler will likely give you a warning, if not an error, on the ‘: 17’ portion saying that the specified bit count exceeds the size of the underlying type. Normally this means that the field will end up being only 16 bits long and you are not getting the 17th bit allocated. So, if you attempt to use the entire 17 bits the top bit will be truncated.
Mixing Types In a Bit Field
What happens when you try to specify the type of single bit fields as a ‘bool’ in C++:
structBitField{ int FirstField:8; bool SecondField:1; int ThirdField:8; int FourthField:8;};
You will be in for an unpleasant surprise with this definition as the behavior in this case is compiler specific. The C++ standard supplies no rules to standardize the behavior here and as such we have an example of Visual Studio and GCC/Clang differences. I could find no documentation about Visual Studio's behavior here and can only write the observed result and the guessed rules which cause it. The size of this bit field is actually 12, Visual Studio seems to close the first int, open a bool type for the single bit then open another int for the last two fields. On the other hand, both GCC and Clang seem to be just fine with packing the bool into the int type and the size of the bit field remains 4 bytes.
Another variation of this, with a different result, could be the following:
structBitField{ int FirstField:8; unsignedintSecondField:8; int ThirdField:8; int FourthField:8;};
If you report the size of this structure, you will get 4 bytes again on the three compilers. Visual Studio does not seem to care if the type is signed or unsigned in this case, it only cares that the fundamental type sizeof is the same.
To be safe, it is suggested not to mix the fundamental types or at least do some serious testing to guarantee the compiler behavior. This is not a compiler bug, the C++ standard does not specify anything of use in clarifying the behavior here, so it is open to interpretation.
The Allowed Fundamental Types
A primary item which my searches failed to show initially was which fundamental types were allowed, most results just showed “unsigned” in examples. When the results were more specific, most of the documentation you find refers to the C99 standard which specifies that the fundamental types can be one of: _Byte, signed int and unsigned int. But what about the C++ standards? This actually took a little digging but the answer is that C++ greatly expanded the allowed types to be: any integral type or enumeration type. So, in C++, fundamental types such as ‘long long’ (64 bit integer on x86) can be used as the type.
The enumeration type is a bit beyond the intended scope but enumerations are considered to be a signed integer type unless you use C++11 class typing on the enumeration. How the compiler interprets mixing the enumeration into the bit field is implementation defined and as such you need to test your compiler behavior.
By these definitions the prior examples, in C99, would have been flagged as warnings or errors due to the use of unsigned short. Though, most compilers did support this and other variations.
Bit Field Binary Representation
Mapping the bit fields to their binary representations is a compiler specific item, so this section may need to be researched for your compiler. On most modern compilers though (MSVC, GNU and Clang targeting x86/x64 code as examples), the general rule is that the fields take bits from the fundamental type in the order you specify starting with the first field taking the lowest bits and continuing up till ending the bit field or moving to the next fundamental type. So, for instance, our original example will have the following binary representation:
structBitField{ unsignedshort Count:8; unsignedshort Offset:7; unsignedshort Inverted:1;};

Fine Grained Bit Field Control
Packing bits tightly is only one of the abilities of a bit field. Additionally, you can insert padding and also control at what points a new fundamental type is allocated. We’ll use an example of mapping a hypothetical binary image format header to a bit field for easier manipulation and access. We’ll start with a textual description of the intentionally horrible image format header chunk:
Image Format:
Byte 0-1: Magic identifier: 0xf321
Byte 2: Version of format. Valid formats 0-5.
Byte 3: low nibble specifies x origin, high nibble specifies y origin. 0=top or left, 1=bottom or right.
Byte 4-7: Width of image. (Little endian.)
Byte 8-11: Height of image. (Little endian.)
Using bit fields we can define this as a structure which can be binary loaded and saved on a little endian CPU. The largest fundamental type described here is a 32 bit integer, so we want to end up with the width and height fields being represented as full integer values. Yet, at the same time we want to keep the bit counts we specify for the fields appropriate to the data ranges specified in the format. For instance, we know the valid formats are 0-5 so the first byte only has 3 bits of range involved. A naive method of mapping the description to a bit field would be to insert padding manually as follows:
structHeader{ int Magic :16; int Version :3; int pad0 :5; // Padding to next byte. int YOrigin :1; int pad1 :3; // Padding to next nibble. int XOrigin :1; int Width :32; // Will be in the next 'int' automatically since it won't fit in the prior one. int Height :32; // Next int again.};
Personally, I don’t like the unused ‘pad’ fields in my code, much less in an auto complete list if your editor supports such things. Additionally, I’d rather be explicit in expecting width to be in the next int as intended. So, we use unnamed fields in the definition to help out here:
structHeader{ int Magic :16; int Version :3; int :5; // Padding to next byte. int YOrigin :1; int :3; // Padding to next nibble. int XOrigin :1; int :0; // Explicitly tell the compiler to allocate a new integer. int Width :32; // Will be in the next 'int' automatically since it won't fit in the prior one. int Height :32; // Next int again.};
This does exactly the same thing but now you don’t have to pepper the structure with ‘padx’ field names unless you have a specific purpose, in which case you could probably use a better name than ‘pad’. Say for instance, you expect to eventually allow more than 8 type versions and thus end up using some of the 5 padding bits. You could name the pad: “VersionReserved”. The name makes sense as it is reserved specifically for extension of the version field. But, assuming you don’t care about the bits for the time being, the unnamed field does the same job and doesn’t dirty up auto completions and such.
What exactly is the unnamed ‘0’ field though, 0 bits, huh? This is a special standards required behavior which tells the compiler to immediately allocate a new fundamental type for the next field to begin filling. While it is already implied that the 32 bit field will have to be placed in a new int since it won’t fit otherwise, this is an explicit hint for readability in this case.
Real World Examples
So all the description is fine, but at this point you may be asking yourself, why would I ever bother with this? There are several cases where a bit field can be extremely valuable, either in simplification or in clearing up messy programming. I’ll give two examples in the following which could be used in today’s coding requirements.
Working With 16 Bit Colors
Working with 16 bit colors can often cause a fair amount of headaches. You pass the color around as an uint16_t (unsigned short) but then need to manipulate the r, g and b components individually. Accessing the components individually involves masking out the relevant portions of the value and then shifting them into place for further work. So, for instance your color is probably packed as 5:6:5 such that there are 5 r and b bits and 6 g bits. Accessing the b bits is simple: “int b = color & 0x1f;”. Accessing r and g involve shifts, so for instance, to get the g you could use: “int g = (color>>5) & 0x3f;”. Replacing items in the colors is more complicated due to having to mask out the original value prior to inserting the new bits. Doing such accesses, even with helpers or macros is often error-prone so, in steps the bit field:
typedefuint16_t ColorRGB565_t;unionColorRGB565{ ColorRGB565_t Composite; struct { ColorRGB565_t B :5; ColorRGB565_t G :6; ColorRGB565_t R :5; };};
So the compiler does all the masking and shifting for you and makes the type a bit cleaner to use. Better yet, by using the bit field you are giving the compiler more opportunity to perform optimizations for you. Perhaps in a function where you extract the G twice, if you use shifts and masking yourself or a helper function, the compiler may not be able to recognize that they are both doing the same thing and eliminate one of the extractions. With the bit field, it is much more likely that the compiler will notice the duplication and remove it. But, considerably better, is that all the shifting and masking is handled by the compiler without hassles for the programmer.
Working With IEEE 754 Floating Points
Eventually, all programmers should probably understand the floating point format. But much as in the 16 bit color example, extracting and manipulating the bits in a float is both error-prone and often confusing. So, it is the bit field definition to the rescue once again:
typedefuint32_t FloatBinaryRep_t;unionFloatBinaryRep{ float Value; struct { FloatBinaryRep_t Mantissa :23; FloatBinaryRep_t Exponent :8; FloatBinaryRep_t Sign :1; };};
Using this union allows you to write simplified code for several things. Duplicating some items in the standard libraries for instance, you could detect nan’s using the following code:
boolIsNan(float f ){ FloatBinaryRep_t fbr; fbr.Value= f; if( fbr.Exponent=0xFF&& fbr.Mantissa!=0) returntrue; returnfalse;}
More important uses are beyond the scope of this article but an example would be implementing a tolerant equivalence check which scales with the magnitudes of the inputs. This is an important feature since the standard tolerance used by many programs is something like “abs( a-b ) > tolerance” which has to be specifically coded for the input data. If your values range from 1-100 the tolerances are likely in the ‘0.0001f’ range, but if your values are 0-1, the tolerance may need to be more like ‘0.00000001f’ to be useful. A more flexible tolerance is one which understands the binary representation and works as a percentage of difference instead of the fixed range used in the simple delta comparisons.
Conclusion
Hopefully you have a better understanding of bit fields, their possible uses and of course the idiosyncrasies of their implementations. Bringing all of the information into one place, with examples beyond the trivial, was the primary goal. Hopefully this short article will be a reasonable reference for people in the future.
Article Update Log
16 April 2013: Rewrite of mixing types. Tracked down a recent C++ standard, this is completely compiler specific and my testbed did not flag the problem due to a bug in my testbed.15 April 2013: First pass clarification of binary representation.
13 April 2013: Initial release.
License
GDOL (Gamedev.net Open License)