2019独角兽企业重金招聘Python工程师标准>>> ![]()
用一句话简单概括一下线性回归:
线性回归是要求一个函数,通过这个函数来预测一个值。
举个例子,比如你要去银行贷款,那银行肯定不能随便给你钱吧。假设,银行会根据3个指标来决定带给你的额度:工资,年龄,房产,分别设为x1x1,x2x2,x3x3,这些就是我们的特征,再设Y为银行借给我们的钱。于是,可以得到:
Y=θ0+θ1x1+θ2x2+θ3x3Y=θ0+θ1x1+θ2x2+θ3x3
.
其中,thetaithetai就是这个线性回归模型的参数了,分别表示同特征对贷款额度的影响程度,比如theta1=10,theta2=100,theta3=1000theta1=10,theta2=100,theta3=1000,那所表明的意思就是房产占的比重最大,年龄其次。theta0theta0叫做偏置项,可以理解成根据贷款之前银行偏于借的多还是借的少,这个跟每个去银行借款的个人没有关系。
线性回归就是找到最合适的一条线(可以想象一个高维),来最好的拟合我们的数据点。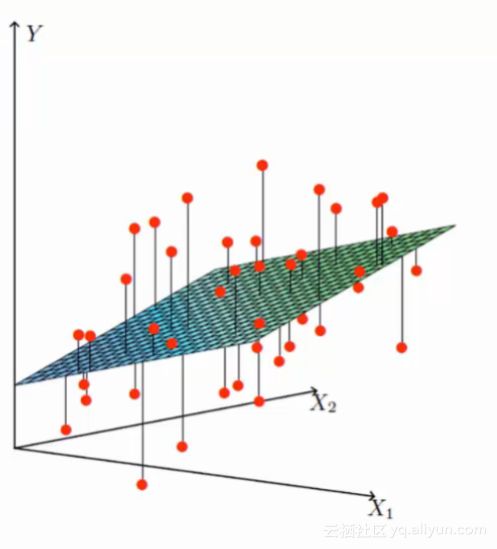
拟合的平面:hθ(x)=θ0+θ1x1+θ2x2+θ3x3hθ(x)=θ0+θ1x1+θ2x2+θ3x3.
整合一下:htheta(x)=sumni=0thetaixi=thetaTxhtheta(x)=sumi=0nthetaixi=thetaTx(其中,x0=1x0=1)
真实值和预测值之间肯定是要存在误差的,我们用εε表示。
对于每个样本:y(i)=θTx(i)+ε(i)y(i)=θTx(i)+ε(i).
误差varepsilon(i)varepsilon(i)是独立并且具有相同分布,根据大数定理,服从均值为0,方差为theta2theta2的高斯(正态)分布。
独立可以这么理解,小明和小红一起贷款,他俩是没关系的。同分布的意思可以可解为他俩都是来的一家银行贷款的,都服从这家银行的规则。正态分布,银行可能多给也可能少,但是绝大多数情况下这个浮动不会太大,极小情况下浮动会比较大,但属于正常情况。
数学分析:
预测值和误差:y(i)=θTxi+ε(i)y(i)=θTxi+ε(i) (1)
由于误差服从正态分布:p(ε(i))=12π√σexp(−(ε(i))22σ2)p(ε(i))=12πσexp(−(ε(i))22σ2) (2)
将(1)带入(2)中:p(y(i)|x(i);θ)=12π√σexp(−(y(i)−θTx(i))22σ2)p(y(i)|x(i);θ)=12πσexp(−(y(i)−θTx(i))22σ2)
因为我们要跟银行贷款,但不知道银行能给我们多少额度,肯定的银行不会告诉你这些参数,于是我们就要通过似然函数来求参数。
似然函数,之前说贝叶斯的时候理论讲的很清楚了。今天又看见一个特别好的CSDN博客,但是公式是用照片传上来的,我把公式重新编辑了一下,转载来**白水东城-最大似然估计学习总结------MadTurtle(转载)了( ̄︶ ̄)↗
似然函数:L(θ)=∏mi=1p(yi|xi;θ)=∏mi=112π√σexp(−(y(i)−θTx(i))22σ2)L(θ)=∏i=1mp(yi|xi;θ)=∏i=1m12πσexp(−(y(i)−θTx(i))22σ2)
这里简单解释一下似然函数的意思,似然是知道了大概是啥分布,但参数不知道,我们根据结果去求什么样的参数能使得到这个结果的概率最大。又因为要对每一个样本都成立,所以所求到的参数不光是使小王在银行取钱符合正态分布,也要使对于小明一样,所以就要把每一个结果(也就是y(i)y(i))在这个参数下的概率都是最大,因此连乘。
对数似然: logL(θ)=log∏mi=112π√σexp(−(y(i)−θTx(i))22σ2)logL(θ)=log∏i=1m12πσexp(−(y(i)−θTx(i))22σ2)
化简得:mlog12π√σ−12σ2∑mi=1(y(i)−θTx(i))2mlog12πσ−12σ2∑i=1m(y(i)−θTx(i))2
最后我们当然要求最大似然,因此即求:
J(θ)=∑i=1m(y(i)−θTx(i))2J(θ)=∑i=1m(y(i)−θTx(i))2
的最小值。上式不正就是最小二乘吗?数学原理原来是这样~~
下面就是求使上式(最小二乘,也就是能拟合的平面)最小的θθ值了。
目标函数:J(θ)=∑mi=1(hθ(x(i))−y(i))2=(Xθ−y)T(Xθ−y)J(θ)=∑i=1m(hθ(x(i))−y(i))2=(Xθ−y)T(Xθ−y) (加粗的使表示矩阵或向量)
对thetatheta求偏导:triangledownthetaJ(theta)=0triangledownthetaJ(theta)=0
得:θ=(XTX)−1XTy
阅读原文http://click.aliyun.com/m/41274/