LeetCode-栈篇

439.三元表达式解析器

给定一个以字符串表示的任意嵌套的三元表达式，计算表达式的值。你可以假定给定的表达式始终都是有效的并且只包含数字 0-9, ?, :, T 和 F (T 和 F 分别表示真和假）。

示例:

输入： “T?2:3”
输出： “2”
解释： 如果条件为真，结果为 2；否则，结果为 3。

输入： “F?1:T?4:5”
输出： “4”
解释： 条件表达式自右向左结合。使用括号的话，相当于：
  “(F ? 1 : (T ? 4 : 5))”         “(F ? 1 : (T ? 4 : 5))”
-> “(F ? 1 : 4)”            -> “(T ? 4 : 5)”
-> “4”               -> “4”

思路:
利用栈,反方向输入字符串,当遇到?的时候,先往前读取T/F, 然后从栈中取出true和false的结果, 然后根据读取的T/F重新选择压入结果

 string parseTernary(string expression) {
        stack<char> stack;
        for (int i = expression.size() - 1 ; i >= 0; i--) {
            // 找到?
            if (expression[i] != '?') {
                stack.push(expression[i]);
                continue;
            }
            // 读取T或F
            char flag = expression[i-1];
            // 因为已经读取的T/F所以要向前移
            i--;
            // 取出T的结果
            char trueResult = stack.top();
            // 退出两个,到 :
            stack.pop();
            stack.pop();
            // 读取F的结果
            char falseResult = stack.top();
            stack.pop();
            // 判断 重新压入栈
            if (flag == 'T') {
                stack.push(trueResult);
            } else {
                stack.push(falseResult);
            }

        }
        string ans;
        ans += stack.top();
        return ans;
    }

255. 验证前序遍历序列二叉搜索树

给定一个整数数组，你需要验证它是否是一个二叉搜索树正确的先序遍历序列。你可以假定该序列中的数都是不相同的。

      5
    /   \
   2    6
  /   \
 1   3
示例:

输入: [5,2,6,1,3]
输出: false

输入: [5,2,1,3,6]
输出: true

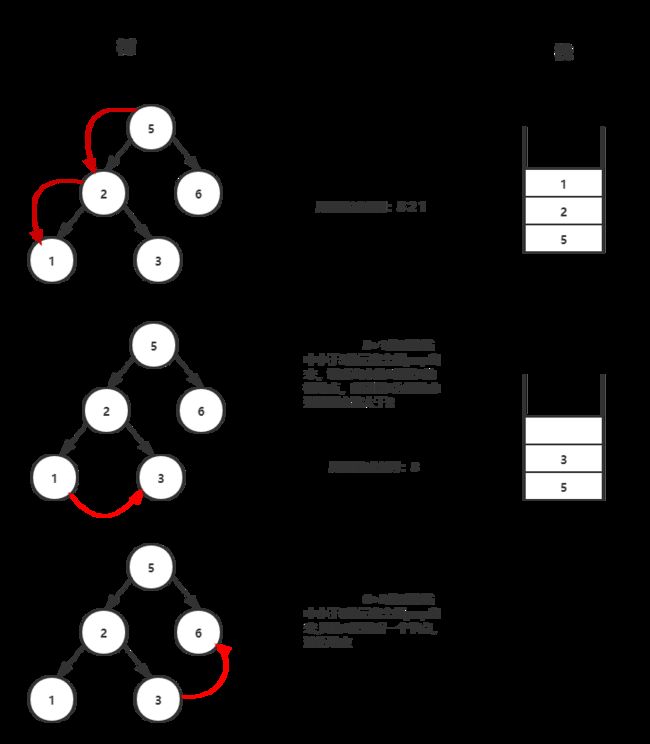
思路:
因为是二叉搜索树,所以左子树都比右子树大
先序遍历: root->左子树->右子树, 所以先是递减然后递增
利用单调栈原理,让这个栈是递减的, 当遇到新的元素比栈顶大的时候,先记录栈顶元素root, 然后逐渐pop元素,直到大于这个元素的栈顶
当发现这个元素 > root的时候 return false, 因为元素大于栈顶的时候是右子树, 而root则是右子树的节点, 必须是 root < 这个元素
继续进栈

bool verifyPreorder(vector<int>& preorder) {
        stack<int> stack;
        int root = INT_MIN;
        for (int i = 0; i < preorder.size(); ++i) {
            while (!stack.empty() && preorder[i] > stack.top()) {
                // 当pop完后root记录的是右子树的结点
                root = stack.top();
                stack.pop();
            }
             //待入栈的是右子树的,所以必须要大于结点 否则false
            if (preorder[i] < root) {
                return false;
            }  
            stack.push(preorder[i]);
        }
        return true;
    }

20.有效括号

给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串，判断字符串是否有效。
有效字符串需满足：左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。注意空字符串可被认为是有效字符串。

示例 2:
输入: “()[]{}”
输出: true

示例 3:
输入: “(]”
输出: false

思路
利用栈,首先遍历字符串 遇到(、[、{的直接将)、]、}入栈
遇到)、]、}的与栈顶比较,如果不同则是false

bool isValid(string s) {
        if (s.size() % 2 != 0) return false;
        stack<char> stack;
        for (int i = 0 ; i < s.size(); i++) {
            if (s[i] == '(') {
                stack.push(')');
            } else if (s[i] == '[') {
                stack.push(']');
            } else if (s[i] == '{') {
                stack.push('}');
            }
            if ((s[i] == ')' || s[i] == '}' || s[i] == ']')) {
                if (stack.empty() || s[i] != stack.top()) {
                    return false;
                }
                stack.pop();
            } 
        }
        return stack.empty();
    }

二叉树前中后序迭代遍历

给定一个二叉树，返回它的中序 遍历。
示例:
输入: [1,null,2,3]
      1
        \
        2
        /
      3
输出: [1,3,2]

144.二叉树前序遍历

思路
方法1
遍历root~root->left, 沿路添加到vector中,当root变成null的时候退出
栈顶拿出top元素,然后root=top->right从右子树重新开始
方法2
先进root节点,然后先right进栈后left进栈

//方法1 
vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode *> s;
        vector<int> res;
        while (!s.empty() || root) {
            while (root) {
            	// 先加入vector中
                res.push_back(root->val);
                s.push(root);
                root = root->left;
            }
            TreeNode *top = s.top();
            s.pop();
            if (top->right) {
                root = top->right;
            }
        }
        return res;
    }
//方法2
vector<int> preorderTraversal(TreeNode* root) {
    vector<int> ans;
    if(root==NULL) return ans;
    stack<TreeNode*> s;
    s.push(root);
    while(!s.empty()){
        TreeNode* top=s.top();
        s.pop();
        ans.push_back(top->val);
        // 反方向进栈
        if(top->right) s.push(top->right);
        if(top->left) s.push(top->left);
    }
    return ans;
}

94.利用栈实现二叉树中序

思路
先root~root->left开始压入栈中直到root是null
取出栈顶top,加入vector中,判断top是否有右子树,有则cur指针指向right

vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode *> s;
        while (root != nullptr || !s.empty()) {
        	// 收集所有左元素
            while(root != nullptr){
                s.push(root);
                root = root->left;
            }
            //取出栈顶元素
            TreeNode * top = s.top();
            res.push_back(top->val);
            s.pop();
            //如果有右子树,就改变root指向,从右子树重新开始
            if (top->right != nullptr) {
                root = top->right;
            }    
        }
        return res;
    }

145.二叉树的后序遍历

思路
与前序相反,利用栈先进right,后进left

vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode *> st;
        if(!root) return res;
        st.push(root);
        while (!st.empty()) {
            TreeNode * top = st.top();
            st.pop();
            res.push_back(top->val);
            if (top->left) st.push(top->left);
            if (top->right) st.push(top->right);
        }
        //反转一下
        reverse(res.begin(),res.end());
        return res;
    }

103.二叉树的锯齿形层次遍历

给定一个二叉树，返回其节点值的锯齿形层次遍历。Z字形遍历
例如：
给定二叉树 [3,9,20,null,null,15,7],

     3
    /  \
   9    20
  /      \
15       7
返回锯齿形层次遍历如下：
[
  [3],
  [20,9],
  [15,7]
]

思路
分奇偶层
方法1:利用双栈
奇数层: 栈1进行pop, pop出的元素先添加到vector中然后先左元素,然后右元素压入栈2
偶数层: 栈2进行pop,pop出的元素添加到vector中然后先右元素,然后左元素压入栈1

方法2:利用双端队列deque
奇数层: 从队列front拿出元素,然后左元素到右元素添加到尾部
偶数层: 从队列尾部拿元素,右元素到左元素添加到队列头

//利用双栈
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (!root) return res;
        stack<TreeNode*> left,right;
        left.push(root);
        while (!left.empty() || !right.empty()) {
        	// 左栈非空
             if (!left.empty()) {
                res.push_back(vector<int>());
                while (!left.empty()) {
                  TreeNode * top = left.top();
                  left.pop();
                  res.back().push_back(top->val);
                  // 左到右添加到栈2
                  if(top->left) right.push(top->left);
                  if(top->right) right.push(top->right);  
                 }
             }
             // 右栈非空
             if(!right.empty()) {
                res.push_back(vector<int>());
                while (!right.empty()) {
                 TreeNode * top = right.top();
                  right.pop();
                  res.back().push_back(top->val);
                  // 右到左添加到栈1
                  if(top->right) left.push(top->right);  
                  if(top->left) left.push(top->left); 
                 }
             }
        }
        return res;
    }

-----------------------------------------------------------------
// 利用双端队列
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        vector<vector<int>> res;
        deque<TreeNode *> queue;
        if (!root) return res;
        queue.push_back(root);
        int lev = 1;
        while (!queue.empty()) {
            int size = queue.size();
            res.push_back(vector<int>());
            while (size--) {
            	// 奇数层
                if (lev % 2 == 1) {
                    TreeNode * n = queue.front();
                    // 从队列头开始取
                    queue.pop_front();
                    res.back().push_back(n->val);
                    // 左到右添加到队列尾
                    if (n->left) queue.push_back(n->left);
                    if (n->right) queue.push_back(n->right);
                } else {
                    TreeNode * n = queue.back();
                    // 从队列尾开始取
                    queue.pop_back();
                    res.back().push_back(n->val);
                    // 右到左添加到队列首
                    if (n->right) queue.push_front(n->right);
                    if (n->left) queue.push_front(n->left);
                }
            }
            lev++;
        }

        return res;
}

150.逆波兰表达式求值

有效的运算符包括 +, -, *, / 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
说明：
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：
输入: [“2”, “1”, “+”, “3”, “"]
输出: 9
解释: ((2 + 1) * 3) = 9

示例 2:
输入: [“10”, “6”, “9”, “3”, “+”, “-11”, "”, “/”, “*”, “17”, “+”, “5”, “+”]
输出: 22
解释:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

思路
方法1 :利用栈,当遇到+、-、*、/后就从栈退两个,相加后压回栈
方法2 :利用数组来代替栈,遇到+、-、*、/ 就对index-2和index-1进行操作

//栈
int evalRPN(vector<string>& tokens) {
    stack<int> st;
    int left,right;
    for (string str : tokens) {
        char sc = str[0];
        // 可能会有-10这样的数, 取第二个
        if (str.size() > 1) sc = str[1];
        switch (sc) {
            case '+':
                right = st.top();
                st.pop();
                left = st.top();
                st.pop();
                st.push(left+right);
            break;
            case '-':
                right = st.top();
                st.pop();
                left = st.top();
                st.pop();
                st.push(left-right);
                break;
            case '*':
                right = st.top();
                st.pop();
                left = st.top();
                st.pop();
                st.push(left*right);
                break;
            case '/':
                right = st.top();
                st.pop();
                left = st.top();
                st.pop();
                st.push(left/right);
                break;
            default:
                st.push(atoi(str.c_str()));
                break;
        }
    }
    return st.top();
}

//数组
int evalRPN(vector<string>& tokens) {
		vector<int> stack(tokens.size() / 2 + 1,0);
        int index = 0;
        for (string str : tokens) {
            char s = str[0];
            if (str.size() >= 2) s = str[1];
            switch (s) {
                case '+':
                    stack[index - 2] += stack[index - 1];
                    index--;
                    break;
                case '-':
                    stack[index - 2] -= stack[index - 1];
                    index--;
                    break;
                case '*':
                    stack[index - 2] *= stack[index - 1];
                    index--;
                    break;
                case '/':
                    stack[index - 2] /= stack[index - 1];
                    index--;
                    break;
                default:
                    stack[index++] = atoi(str.c_str());
                    break;
            }
        }
        return stack[0];
}

772.基本计算器III

实现一个基本的计算器来计算简单的表达式字符串。
表达式字符串可以包含左括号 ( 和右括号 )，加号 + 和减号 -，非负 整数和空格 表达式字符串只包含非负整数， +, -, *, / 操作符，左括号 ( ，右括号 )和空格 。整数除法需要向下截断。
你可以假定给定的字符串总是有效的。所有的中间结果的范围为 [-2147483648, 2147483647]。

一些例子：
“1 + 1” = 2
" 6-4 / 2 " = 4
“2*(5+52)/3+(6/2+8)" = 21
"(2+6 3+5- (3*14/7+2)*5)+3”=-12

思路
递归+栈
先对()里面字符串提取,然后递归,首先找到()下标
之后对正数直接压栈,负数-num压栈, *、/则提取栈顶元素与当前数计算,然后出栈顶,进计算后的数
循环计算栈所有元素和

int calculate(string s) {
        long int num = 0,  res = 0;
        stack<long> st;
        // 默认第一个先用+
        char ch = '+';
        for (int i = 0 ; i < s.size(); i++) {
            if (s[i] >= '0' && s[i] <= '9') {
                num = num * 10 + s[i] - '0';
            } else if (s[i] == '(') {
                int j = i;
                int cnt = 0;
                for (; i < s.size(); i++) {
                    // 寻找配对的() 
                    if (s[i] == '(') cnt++;
                    if (s[i] == ')') cnt--;
                    // 当( 数量和 ) 相同的时候,进入递归
                    if (cnt == 0) {
                        // 将() 部分的形成新的字符串
                        num = calculate(s.substr( j + 1,i - j - 1));
                        break;
                    }

                }

            }
            // ASCII码中+-*/都小于 '0'
            //如 1+2+  这样判断是遇到第二个+号,而ch记录的是前一个+号
            if ((s[i] < '0' && s[i] != ' ') || i == s.size() - 1) {
                if (ch == '+') {
                    st.push(num);
                } else if (ch == '-') {
                    st.push(-num);
                } else if (ch == '*' || ch == '/') {
                    long int top = (ch == '*') ? st.top() * num : st.top() / num;
                    st.pop();
                    st.push(top);
                }
                // 变成第二个操作符
                ch = s[i];
                num = 0;
            }
        }

        while (!st.empty()) {
            num += st.top();
            st.pop();
        }
        return num;
    }

42.接雨水

定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

思路
利用单调递减栈, 当出现比栈顶低的柱子就进栈,当出现比栈顶更高的柱子的时候, 先进行第一次出栈得到底部高度h,再出栈一次得到left, 然后取两个柱子更低的那个作为H, 雨水就是 (H-h) * (right_index - left_index - 1)
逐层逐层计算

class Column {
public:
	  int index;
	  int height;   
	  Column (int i = 0, int h = 0) : index(i),height(h){}
};
int trap(vector<int>& height) {
   int res = 0;
   stack<Column> st;
   for (int i = 0 ; i < height.size(); i++) {
   	   // 利用循环 一层一层计算 如 2 1 0 1 3
   	   // 0->1的时候就计算1次了,此时栈有21 
   	   //当出现3的时候以1为底2~3之间进行计算,只计算一层
       while (!st.empty() && height[i] > st.top().height) {
         // 获得底高
          Column cur = st.top();
          st.pop();
          if (st.empty()) break;
          // cur的上一个更高的柱子
          Column left = st.top();
          int r = i;
          int h = min(height[r],left.height) - cur.height;
          res += (r - left.index - 1) * h; 
       } 
       // 加入栈
        st.push(Column(i,height[i]));
   }
   return res;
}

84.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。


示例:
输入: [2,1,5,6,2,3]
输出: 10

思路
利用单调栈, 单调递增
当遇到 > 栈顶的元素直接进栈
当遇到 < 栈顶的元素,逐渐退栈直到栈顶 < 新元素
维持单调递增栈
在退栈过程中叶逐渐计算面积

 int largestRectangleArea(vector<int>& heights){
    int ans = 0;
    stack<int> st;
    // 构造递增栈 开头添加0 ,形成递增
    heights.insert(heights.begin(), 0);
    // 结尾添加0,用于结算
    heights.push_back(0);
    for (int i = 0; i < heights.size(); i++)
    {
        // 当有元素比栈顶低的时候, 逐渐退栈
       while (!st.empty() && heights[st.top()] > heights[i]) {
          // 获取当前栈顶的index
            int curH = heights[st.top()];
            //退了
            st.pop();
            // 这个left实际就是上一个max值的index
            int left = st.top() + 1;
            int right = i - 1;
            // 计算宽度
            int len = right - left + 1;
            ans = max(ans, len  * curH );
       }
       st.push(i);
    }
    return ans;
}

173.二叉搜索树迭代器

实现一个二叉搜索树迭代器。你将使用二叉搜索树的根节点初始化迭代器。调用 next() 将返回二叉搜索树中的下一个最小的数。

BSTIterator iterator = new BSTIterator(root);
iterator.next(); // 返回 3
iterator.next(); // 返回 7
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 9
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 15
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 20
iterator.hasNext(); // 返回 false

class BSTIterator {
public:
    stack<TreeNode *> st;
    BSTIterator(TreeNode* root) {
        TreeNode *node = root;
        get_nodes(node,st);
    }
    // 左子树全部进栈
    void get_nodes(TreeNode * root,stack<TreeNode *> & st) {
        while (root) {
            st.push(root);
            root = root->left;
        }
    }
    /** @return the next smallest number */
    int next() {
        TreeNode* now = st.top();
        st.pop();
        int ans = now -> val; // 若有右子树，压入栈内
        if(now -> right)  {
            now = now->right;
            // 右节点进入,收集左节点
            get_nodes(now,st);
        }
        return ans;
    }

    /** @return whether we have a next smallest number */
    bool hasNext() {
        return !st.empty();
    }
};

1063.有效子数组的数目

给定一个整数数组 A，返回满足下面条件的 非空、连续 子数组的数目：
子数组中，最左侧的元素不大于其他元素。
示例 1：

输入：[1,4,2,5,3]
输出：11
解释：有 11 个有效子数组，分别是：[1],[4],[2],[5],[3],[1,4],[2,5],[1,4,2],[2,5,3],[1,4,2,5],[1,4,2,5,3] 。

思路
利用单调栈,当出现新元素比栈顶小的时候,根据条件最左侧元素不大于其他元素,那么栈顶index到新元素index - 1距离就是一个有效子数组数目

int validSubarrays(vector<int>& nums) {
        if (nums.size() < 2) return nums.size();
        int res = 0;
        stack<int> st;
        int N = nums.size();
        for (int i = 0; i < N; ++i) {
            // 如果栈顶 > nums[i] 由于最左侧不大于其他数
            //那么区间就是 栈顶index ~ i-1 
            while (!st.empty() && nums[st.top()] > nums[i]) {
                res += i - st.top();
                st.pop();
            }
            st.push(i);
        }
        // 栈中剩余元素都是递增的,那么到尾部之间的元素都是栈顶最小
        // 所以栈顶到尾的数量就是该区间子数组数量
        while (!st.empty()) {
            res += N - st.top();
            st.pop();
        }
        return res;
}