LeetCode-排序篇

1086.前五科的平均分数

给你一个不同学生的分数列表，请按 学生的 id 顺序 返回每个学生最高的五科 成绩的 平均分。对于每条 items[i] 记录， items[i][0] 为学生的 id，items[i][1] 为学生的分数。平均分请采用整数除法计算。

思路
先按学号从小到大排序,学号相同则按分数大到小排序

static bool compare(vector<int> &a, vector<int> &b) {
        if(a[0] < b[0])
            return true;
        if(a[0] > b[0])
            return false;
        return a[1] > b[1];
    }
    vector<vector<int>> highFive(vector<vector<int>>& items) {
        sort(items.begin(), items.end(), compare);
        vector<vector<int>> ans;
        int cout = 0;
        int sum = 0;
        for (int i = 0 ; i < items.size(); i++) {
            if (cout < 5) {
                sum += items[i][1];
                cout++;
            }
            if ( i == (items.size() - 1) || items[i][0] != items[i+1][0] ) {
                vector<int> vt ;
                vt.push_back(items[i-1][0]);
                vt.push_back(sum / cout);
                ans.push_back(vt);
                cout = 0;
                sum = 0;
            }
        }
        return ans;
    }

252.会议室

给定一个会议时间安排的数组，每个会议时间都会包括开始和结束的时间 [[s1,e1],[s2,e2],…] (si < ei)，请你判断一个人是否能够参加这里面的全部会议。
示例 1:
输入: [[0,30],[5,10],[15,20]]
输出: false
示例 2:
输入: [[7,10],[2,4]]
输出: true

思路
首先根据[0]值从小到大排序
然后如果第二个值的[0] < 第一个值的[1] 则表示冲突

static bool compare(vector<int> &a, vector<int> &b) {
        if (a[0] > b[0]) return false;
        return true;
    }
    bool canAttendMeetings(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end(), compare);
        for (int i = 1; i < intervals.size(); i++) {
            if (intervals[i-1][1] > intervals[i][0]) return false;
        }

        return true;
    }

253.会议室II

给定一个会议时间安排的数组，每个会议时间都会包括开始和结束的时间 [[s1,e1],[s2,e2],…] (si < ei)，为避免会议冲突，同时要考虑充分利用会议室资源，请你计算至少需要多少间会议室，才能满足这些会议安排。
示例 1:
输入: [[0, 30],[5, 10],[15, 20]]
输出: 2
示例 2:
输入: [[7,10],[2,4]]
输出: 1

思路
首先根据[0]进行从小到大排序,然后按[1]进入小顶堆
此时小顶堆上的[1]是结束时间最短的
然后新元素的开始时间[0]与小顶堆堆顶比较,如果是大于小顶堆,那么就pop堆顶,新元素进堆,因为开始时间>结束时间所以可以视为是同个会议室
计算堆里元素即为会议室个数

static bool cmp(vector<int>a, vector<int> b){
        return a[0] < b[0];
}
int minMeetingRooms(vector<vector<int>>& intervals) {
        if(intervals.size() == 0 || intervals[0].size() == 0)
            return 0;
        sort(intervals.begin(), intervals.end(), cmp);
        // greater表示是小顶堆
        priority_queue<int, vector<int>, greater<int>> occupied;   
        for(auto meet:intervals){
            // 堆顶是结束时间最前的
            // 新元素的开始时间 > 堆顶结束时间就说明这两个可以同个会议室
            if(!occupied.empty() && occupied.top() <= meet[0]) {
                occupied.pop();
            }  
            occupied.push(meet[1]);  //当前会议结束时间入队
        }
        return occupied.size();
}

280.摆动排序

给你一个无序的数组 nums, 将该数字 原地 重排后使得 nums[0] <= nums[1] >= nums[2] <= nums[3]…。

示例:
输入: nums = [3,5,2,1,6,4]
输出: 一个可能的解答是 [3,5,1,6,2,4]

思路
1:先排序,然后根据下标偶数的时候与后面一个换一下
2:不需要先排序,下标奇数的时候判断时候>=下一个,如果不是就互换

void swap(vector<int>& nums,int i,int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
    void wiggleSort(vector<int>& nums) {
        for (int i = 1; i < nums.size(); i++) {
            //偶数的时候,如果大于后者,那么就需要换
            // 奇数的时候,如果小于后者,那么就需要换
            if ((i % 2 == 0 && nums[i] > nums[i - 1]) || (i % 2 == 1 && nums[i] < nums[i - 1])) {
                swap(nums,i,i - 1);
            }
        }
    }

324.摆动排序II

给定一个无序的数组 nums，将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。

示例 1:
输入: nums = [1, 5, 1, 1, 6, 4]
输出: 一个可能的答案是 [1, 4, 1, 5, 1, 6]
示例 2:
输入: nums = [1, 3, 2, 2, 3, 1]
输出: 一个可能的答案是 [2, 3, 1, 3, 1, 2]

思路
先进行排序,然后将数组分两部分,根据index的奇偶,在偶数的时候从前部分最后一个放数组[0]位置,奇数就后半部分最后一个放数组[1]
这样就能变成 [0]<[1]>[2]<[3]

void wiggleSort(vector<int>& nums) {
        int size = nums.size();
        vector<int> tmp(nums);
         //size+1原因是前部分较小,数量比后半段多1个情况下可以放两边
         // 如果后半段多的话放不了
         //如12121, 1有3个,2有2个. 11122则mid要[2]才可以
        int end = size-1, mid = (size + 1) / 2 - 1;
        sort(tmp.begin(), tmp.end());
        for (int i = 0; i < size; ++i) {
            nums[i] = i % 2 == 0 ? tmp[mid--] : tmp[end--];
        }
    }

1057.校园自行车分配

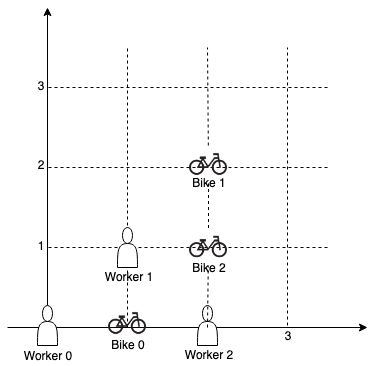
在由 2D 网格表示的校园里有 n 位工人（worker）和 m 辆自行车（bike），n <= m。
所有工人和自行车的位置都用网格上的 2D 坐标表示。
我们需要为每位工人分配一辆自行车。在所有可用的自行车和工人中，我们选取彼此之间曼哈顿距离最短的工人自行车对 (worker, bike) ，并将其中的自行车分配給工人。如果有多个 (worker, bike) 对之间的曼哈顿距离相同，那么我们选择工人索引最小的那对。类似地，如果有多种不同的分配方法，则选择自行车索引最小的一对。不断重复这一过程，直到所有工人都分配到自行车为止。
给定两点 p1 和 p2 之间的
曼哈顿距离为 Manhattan(p1, p2) = |p1.x - p2.x| + |p1.y - p2.y|。
返回长度为 n 的向量 ans，其中 a[i] 是第 i 位工人分配到的自行车的索引（从 0 开始）。

示例

输入：workers = [[0,0],[1,1],[2,0]], bikes = [[1,0],[2,2],[2,1]]
输出：[0,2,1]
解释：
工人 0 首先分配到自行车 0 。工人 1 和工人 2 与自行车 2 距离相同，因此工人 1 分配到自行车 2，工人 2 将分配到自行车 1 。因此输出为 [0,2,1]。

思路
首先计算每个worker到bike的距离d,然后将d为key,worker_id和bike_id存到Map中
然后遍历这个Map,遍历是从0开始的,所以是距离最短的先

vector<int> assignBikes(vector<vector<int>>& workers, vector<vector<int>>& bikes) {
        vector<int> ans(workers.size());
        //key是d
        //pair:worker_id , bike_id
        map<int, vector<pair<int, int>>> distMap;
        vector<bool> wUsed(workers.size(), false);
        vector<bool> bUsed(bikes.size(), false);

        for (int wIdx = 0; wIdx < workers.size(); ++wIdx) {
            for (int bIdx = 0; bIdx < bikes.size(); ++bIdx) {
            // 计算距离
                int d = abs(workers[wIdx][0] - bikes[bIdx][0]) + abs(workers[wIdx][1] - bikes[bIdx][1]);
                distMap[d].push_back({wIdx, bIdx});
            }
        }

        for (auto it = distMap.begin(); it != distMap.end(); ++it) {
            for (auto p : it->second) {
                int worker = p.first;
                int bike = p.second;
                if (wUsed[worker] || bUsed[bike])
                    continue;
                ans[worker] = bike;
                wUsed[worker] = true;
                bUsed[bike] = true;
            }
        }

        return ans;
    }

1244.力扣排行榜

请你帮忙来设计这个 Leaderboard 类，使得它有如下 3 个函数：
addScore(playerId, score)：
假如参赛者已经在排行榜上，就给他的当前得分增加 score 点分值并更新排行。
假如该参赛者不在排行榜上，就把他添加到榜单上，并且将分数设置为 score。
top(K)：返回前 K 名参赛者的 得分总和。
reset(playerId)：将指定参赛者的成绩清零。题目保证在调用此函数前，该参赛者已有成绩，并且在榜单上。
请注意，在初始状态下，排行榜是空的。

输入：
[“Leaderboard”,“addScore”,“addScore”,“addScore”,“addScore”,“addScore”,“top”,“reset”,“reset”,“addScore”,“top”]
[[],[1,73],[2,56],[3,39],[4,51],[5,4],[1],[1],[2],[2,51],[3]]
输出：
[null,null,null,null,null,null,73,null,null,null,141]

解释：
Leaderboard leaderboard = new Leaderboard ();
leaderboard.addScore(1,73); // leaderboard = [[1,73]];
leaderboard.addScore(2,56); // leaderboard = [[1,73],[2,56]];
leaderboard.addScore(3,39); // leaderboard = [[1,73],[2,56],[3,39]];
leaderboard.addScore(4,51); // leaderboard = [[1,73],[2,56],[3,39],[4,51]];
leaderboard.addScore(5,4); // leaderboard = [[1,73],[2,56],[3,39],[4,51],[5,4]];
leaderboard.top(1); // returns 73;
leaderboard.reset(1); // leaderboard = [[2,56],[3,39],[4,51],[5,4]];
leaderboard.reset(2); // leaderboard = [[3,39],[4,51],[5,4]];
leaderboard.addScore(2,51); // leaderboard = [[2,51],[3,39],[4,51],[5,4]];
leaderboard.top(3); // returns 141 = 51 + 51 + 39;

提示：
1 <= playerId, K <= 10000
题目保证 K 小于或等于当前参赛者的数量
1 <= score <= 100
最多进行 1000 次函数调用

class Leaderboard {
private:
	//一种Set,里面内容时有序的且可以重复
    multiset<int> rank;
    //判断
    array<int, 10001> record{};
public:
    Leaderboard() {
    }
    void addScore(int playerId, int score) {
    // 引用修改
       auto &num = record[playerId];
       if (num == 0) {
           rank.emplace(score);
       } else {
           rank.erase(rank.find(num));
           rank.emplace(score + num);
       }
       num += score;
    }
    int top(int K) {
        int ans = 0;
        auto it = --rank.end();
        while(K--) {
            ans += *it;
            it--;
        }
        return ans;
    }
    void reset(int playerId) {
        auto & num = record[playerId];
        rank.erase(rank.find(num));
        num = 0;

    }

};

56.合并区间

给出一个区间的集合，请合并所有重叠的区间。

示例 1:
输入: [[1,3],[2,6],[8,10],[15,18]]输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

思路
先排序,按照[0]从小到大
然后判断左边元素[1]和右边元素[0]谁大,左边大则判断左边元素[1]和右边元素[1]谁大,
如果左边元素[1] < 右边元素[0],就是新元素

 static bool cmp(const vector<int> &a,const vector<int> & b) {
    if (a[0] < b[0]) return true;
    else if (a[0] > b[0]) return false;
    return a[1] < b[1];
}
vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> ans;
        sort(intervals.begin(),intervals.end(),cmp);
        for (int i = 0 ; i < intervals.size(); ) {
            auto it = intervals[i];
            int j = i + 1;
            for (; j < intervals.size(); j++) {
                auto m = intervals[j];
                // 此时两个区间不可合并
                if (it[1] < m[0]) break;
                // 判断第二个元素[1]是否>第一个元素[1]
                if (it[1] < m[1]) {
                    it[1] = m[1];
                }
            }
            // 加入
            ans.push_back(it);
            i = j;
        }
        return ans;
 }

179.最大数

给定一组非负整数，重新排列它们的顺序使之组成一个最大的整数。

示例 1:
输入: [10,2]
输出: 210
示例 2:
输入: [3,30,34,5,9]
输出: 9534330

思路
转换为字符串进行排序

static bool cmp(int a,int b) {
        string A = to_string(a);
        string B = to_string(b);
        // 看哪种排列大
        return (A + B) > (B + A);
    }
    string largestNumber(vector<int>& nums) {
        string ans;
        // 直接进行排列
        sort(nums.begin(),nums.end(), cmp);
        for (int n : nums) {
            ans += to_string(n);
        }
        if (atoi(ans.c_str()) == 0) {
            ans = ("0");
        }
        return ans;
    }

57.插入区间

给出一个无重叠的 ，按照区间起始端点排序的区间列表。
在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

示例 1:
输入: intervals = [[1,3],[6,9]], newInterval = [2,5]
输出: [[1,5],[6,9]]
示例 2:
输入: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出: [[1,2],[3,10],[12,16]]
解释: 这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。

思路
首先寻找与newInterval冲突的区间,如果冲突了先把newInterval添加进去
从冲突的i开始,将后面的区间与result最后一个区间比对,如果冲突就修改

vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
        vector<vector<int>> result;
    	int i;
		// 寻找冲突区间,如果冲突,那么把newInterval加入
    	for (i = 0; i < intervals.size(); ++i) {
			// newInterval起始 > intervals末
    		if (newInterval[0] > intervals[i][1]) {
    			result.push_back(intervals[i]);
    		} else {
    			break;
    		}
    	}
		// 加入冲突的
    	result.push_back(newInterval);
		// 循环合并,从上面冲突的i开始
    	for (; i < intervals.size(); ++i) {
    		// 没冲突
    		if (result.back()[1] < intervals[i][0]) {
    			result.push_back(intervals[i]);
    		} // 冲突了,重新构造区间
    		else {
				result.back()[0] = min(result.back()[0], intervals[i][0]);
				result.back()[1] = max(result.back()[1], intervals[i][1]);
    		}
    	}
    	
	return result;
    }

349.两个数组交集

给定两个数组，编写一个函数来计算它们的交集。

示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [9,4]

思路
创建一个Map,将nums1数据复制进Map中
遍历nums2, 如果map中找得到,那么删除 并将该数添加到ans中

vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
   		//map是红黑树,查找是二分, unordered_set是hash,查找O(1)
        unordered_set<int> m(nums1.begin(), nums1.end());   ////将第一个数组的元素建立一个unordered_set
        vector<int> res;  //建立关于结果的vector

        for(int a:nums2)
        {
            if(m.erase(a))    //既查找了m中是否存在a,又完成了删除a的工作，避免后续过程重复元素
            {
               res.push_back(a);  //在vector res的末尾加入a
            }
        }
        return res;
    }

350.两个数组的交集II

给定两个数组，编写一个函数来计算它们的交集。

示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]

思路
使用unordered_set将nums1元素为key,value为0添加
当nums1重复的key,那么就value++
之后从nums2位key取, 有则value–

vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        unordered_map<int,int> m1;
        vector<int> ans;
        for (int num : nums1) {
            m1[num]++;
        }
        for (int num : nums2) {
            if (m1[num] > 0) {
                ans.push_back(num);
                m1[num]--;
            }    
        }
        return ans;
    }

75.颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
注意:
不能使用代码库中的排序函数来解决这道题。
示例:
输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]

思路
1.直接计算0,1,2出现次数,然后遍历一遍
2.双指针,分为left,right。left是等于0的,left-right是等于1的, 大于right是为2的

//方法1,计算0,1,2次数
void sortColors(vector<int>& nums) {
        vector<int> m(3);
        for (int nm : nums) {
            m[nm]++;
        } 
        int index = 0;
        for (int i = 0; i < 3; i++) {
            while (m[i]--) nums[index++] = i;
        }
    } 
// 双指针
void sortColors(vector<int>& nums) {
       int left = 0;
       int right = nums.size() - 1;
       // i > right即可停止
       for (int i = 0 ; i <= right; i++) {
           if (nums[i] == 0) swap(nums[left++],nums[i]);
           if (nums[i] == 2) swap(nums[right--], nums[i--]);//让i减1,之后for会+1
       }
}

147.对链表进行插入排序

示例 1：
输入: 4->2->1->3
输出: 1->2->3->4
示例 2：
输入: -1->5->3->4->0
输出: -1->0->3->4->5

    ListNode* insertionSortList(ListNode* head) {
        if(!head||!head->next)
            return head;
        // 创建临时头
        ListNode * temp = new ListNode(-1);
        temp -> next = head;
        // 创建双指针
        ListNode * pre = head;
        ListNode * next_node = head->next; 

        while(next_node){
            //如果出现降序
            if(next_node->val < pre->val){
                ListNode * cur = temp;
                // 从头寻找那个降序的前一个节点
                while(cur->next &&  cur->next->val < next_node->val){
                    cur = cur->next;
                }
                pre->next = next_node->next;
                next_node->next = cur->next;
                //cur是原next_node的上上个节点
                cur->next = next_node;
                // pre指针没有变,改变next_node
                next_node = pre->next;
            }else{
                pre = pre->next;
                next_node = pre->next;
            }
        }
        return temp->next;
    }

148.排列链表

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5

思路
先两个两个的 merge，完成一趟后，再 4 个4个的 merge，直到结束。举个简单的例子：[4,3,1,7,8,9,2,11,5,6].
step=1: (3->4)->(1->7)->(8->9)->(2->11)->(5->6)
step=2: (1->3->4->7)->(2->8->9->11)->(5->6)
step=4: (1->2->3->4->7->8->9->11)->5->6
step=8: (1->2->3->4->5->6->7->8->9->11)
操作链表的3个技巧
1.虚拟头节点,自己新声明一个头结点
2.merge合并两个List
3.cut将链表切掉前 n 个节点，并返回后半部分的链表头

ListNode* sortList(ListNode* head) {
        ListNode temp(0);
        temp.next = head;
        int len = 0;
        while (head) {
            len++;
            head = head->next;
        }
        for (int size = 1; size < len; size *= 2) {
            // 开始节点
            ListNode *start = temp.next;
            //用来连接已经排序好的
            ListNode *tail = &temp;
            while (start) {
                ListNode *l1 = start;
                ListNode *l2 = cut(start, size); // l1->@->@  l2->@->@->@...
                // start是l2断开的后一个节点开始
                start = cut(l2,size); // l1->@->@  l2->@->@    start->@->@.....
                //将排好序的串联起来
                tail->next = merge(l1, l2); // tail->l1->l2
                //寻找尾部,然后接着串联排好序的
                while(tail->next) tail = tail->next; // l1->l2->tail->null
            }
        }
        return temp.next;
    }
    
    //从head开始到n切断,返回切断后一个节点
    ListNode* cut(ListNode* head, int n) {
        auto pre = head;
        while (--n && pre) pre = pre->next;
        if (pre == nullptr) return pre;
        auto next = pre->next;
        pre->next = nullptr;
        return next;
    }
    //从小到大合并链表
    ListNode* merge(ListNode* l1, ListNode* l2) {
        ListNode head(0);
        auto temp = &head;
        while (l1 && l2) {
            if (l1->val > l2->val) {
                temp->next = l2;
                temp = l2;
                l2 = l2->next;
            } else {
                temp->next = l1;
                temp = l1;
                l1 = l1->next;
            }
        }
        temp->next = l1 ? l1 : l2;
        return head.next;
    }

220.存在重复元素III

给定一个整数数组，判断数组中是否有两个不同的索引 i 和 j，使得 nums [i] 和 nums [j] 的差的绝对值最大为 t，并且 i 和 j 之间的差的绝对值最大为 ķ。

示例 1:
输入: nums = [1,2,3,1], k = 3, t = 0
输出: true
示例 2:
输入: nums = [1,0,1,1], k = 1, t = 2
输出: true
示例 3:
输入: nums = [1,5,9,1,5,9], k = 2, t = 3
输出: false

思路
利用set底层是自平衡二叉查找树,支持在 O(h) = O(log n)时间内完成 插入，搜索，删除 操作
set中lower_bound(value)函数可以返回第一个 >= value元素的迭代器,

bool containsNearbyAlmostDuplicate(vector<int>& nums, int k, int t) {
	set<double> _set;
	for (int i = 0; i < nums.size(); ++i) 
	{   
        //lower_bound >=  这个参数 如果有则返回一个迭代器
        //使用double是因为用long存在转换风险
        // 寻找 >= nums[i] - t
		auto s = _set.lower_bound((double)nums[i] - (double)t);
		//找到 >= 的了 然后判断是不是在<= t范围内
		if (s != _set.end() && *s <= (double)nums[i] + (double)t) 
		{
			return true;
		}
		//加入元素
		_set.insert(nums[i]);
        // 保证下标在k范围内,那么元素个数不能大于k
		if (_set.size() > k) 
		{
			_set.erase(nums[i - k]);
		}
	}
	return false;
}

164.最大间距

给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。
如果数组元素个数小于 2，则返回 0。

示例 1:
输入: [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。
示例 2:
输入: [10]
输出: 0
解释: 数组元素个数小于 2，因此返回 0。

方法1思路 桶排序
计算相邻桶间max和min的差值

桶宽度桶的范围由max、min、数组长度决定,而相邻元素间隔最小值是由max-min/间隔数 决定, 如[2,4,6,8,10] 最小的间隔是(10-2)/4 == 2 , 排除这种平均情况的话 相邻元素间距是ans >= 2,这样的话我们不需要考虑桶内宽度是否就是答案,因为这是最小的情况

桶个数=(max-min)/桶宽度 + 1
为什么+1呢
还是举上面的例子，[2,4,6,8], 桶的长度 = (8 - 2) / (4 - 1) = 2
桶的个数 = (8 - 2) / 2 = 3
已知一个元素，需要定位到桶的时候，一般是 (当前元素 - 最小值) / 桶长度
这里其实利用了整数除不尽向下取整的性质
但是上面的例子，如果当前元素是 8 的话 (8 - 2) / 2 = 3，对应到 3 号桶
如果当前元素是 2 的话 (2 - 2) / 2 = 0，对应到 0 号桶
你会发现我们有 0,1,2,3 号桶，实际用到的桶是 4 个，而不是 3 个

 class Bucket {
    public:
        int max = INT_MIN;
        int min = INT_MAX;
    };
    int maximumGap(vector<int>& nums) {
        if (nums.size() < 2) return 0;
        //获取vector中最大最小值
        auto minmax = minmax_element(nums.begin(), nums.end());
        int min = *minmax.first;
        int max = *minmax.second;
        //元素都相等的情况
        if (max == min) return 0;
        //计算桶宽度, (最大-最小)/间隔数
        int bucket_len = (max - min) / (nums.size() - 1);
        //排除0的情况
        bucket_len = std::max(1,bucket_len);
        //桶个数 (最大-最小) / 桶宽度 + 1
        int bucket_nums = (max - min) / bucket_len + 1;
        vector<Bucket> buckets(bucket_nums);
        //将元素放进对应的桶中
        for (int nm : nums) {
            int index = (nm - min) / bucket_len;
            buckets.at(index).max = std::max(buckets.at(index).max, nm);
            buckets.at(index).min = std::min(buckets.at(index).min, nm);
        }
        int leftMax = buckets[0].max;
        int ans = 0;
        for (int i = 1 ; i < bucket_nums; i++) {
            //跳过空桶, 右桶.min - 左桶.max 就是间距
            if (buckets[i].min != INT_MAX) {
                ans = std::max(ans,buckets[i].min - leftMax);
                leftMax = buckets[i].max;
            }
        }
        return ans;
    }

方法二思路 计数排序 leetcode时间太长 过不了,也是一种解法

//计数排序
int maximumGap(vector<int>& nums) {
        if (nums.size() < 2) return 0;
        //寻找max和min
        auto minmax = minmax_element(nums.begin(), nums.end());
        int min = *minmax.first;
        int max = *minmax.second;
        if (max == min) return 0;
        //创建一个新数组
        vector<int> vts(max- min + 1);
        for (int n : nums) {
        	//每个元素-min后的index都会在vts数组范围内
            vts[n - min]++;
        }
        int left = -1;
        int ans = INT_MIN;
        for (int i = 0; i < vts.size(); i++) {
            if (vts[i] != 0) {
                if (left != -1) {
                	//计算间隔长度
                     ans = std::max(ans,i - left);
                } 
                left = i;
            }
            
        }
        return ans;
    }

快排

//最坏情况是O(n²) 升序或降序  
void QuickSort(vector<int> &nums, int low, int high) {
    if (low >= high) return ;
    int left = low;
    int right = high;
    int key = nums[left];
    while (left < right ) {
        // 右往左找第一个小于key的
        while (left < right && nums[right] >= key) right--;
        if (left < right) {
            // 小于key的赋给左边
            nums[left] = nums[right];
            left++;
        }
        //左往右找第一个大于key的
        while (left < right && nums[left] <= key) left++;
        if (left < right) {
            // 大于key的赋给右边
            nums[right] = nums[left];
            right--;
        }
    }
    nums[left] = key;
    //递归左半部分和右半部分
    QuickSort(nums, low, left - 1);
    QuickSort(nums, left + 1, high);
}

堆排

void MakeHeap(vector<int> &nums, int root,int len) {
    int left = root * 2 + 1;
    int max = left;
    if (left < len) {
        int right = left + 1;
        // 左右子树比较
        if (right < len && nums[right] > nums[left]) {
            max = right;
        }
        if (nums[root] < nums[max]) {
            swap(nums, root, max);
            //继续向下递归
            MakeHeap(nums, max, len);
        }
    }
}
void HeapSort(vector<int> &nums,int len){
    //从一半开始,向0调整
    for (int i = len / 2; i >= 0; i--) {
        MakeHeap(nums, i, len);
    }
    //将堆顶向后移,同时减少长度
    for (int i = len - 1; i > 0; i--) {
        swap(nums, 0 , i);
        MakeHeap(nums, 0, i);
    }
}

归并

void Merge(vector<int> &nums, int left, int mid, int right) {
    vector<int> temps;
    int low = left;
    int i = left;
    int j = mid + 1;
    while (i <= mid && j <= right) {
        if (nums[i] < nums[j]) {
            temps.push_back(nums[i++])  ;
        } else {
            temps.push_back(nums[j++])  ;
        }
    }
    while (i <= mid) temps.push_back(nums[i++]);
    while (j <= right) temps.push_back(nums[j++]);
    for (int i = 0 ; i < temps.size(); i++) {
        nums[low++] = temps[i];
    }
}
void MergeSort(vector<int> &nums, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2 ;
        //切成一个一个后排序
        MergeSort(nums, left, mid);
        MergeSort(nums, mid + 1, right);
        Merge(nums,left, mid, right);
    }
}