Gabor滤波器进行纹理分割
Texture-Segmentation-using-Gabor-FiltersGabor
推荐一个对Gabor特征总结很全面的文章：http://mengqi92.github.io/2015/10/11/gabor/
代码地址：https://github.com/mortezamg63/Texture-Segmentation-using-Gabor-Filters
The texture segmentation algorithm in this project involves the following three steps:
• Decomposition of the input image using a filter bank,
• Feature extraction,
• Clustering.
该项目中的纹理分割算法包括以下三个步骤：
•使用滤波器组分解输入图像，
• 特征提取，
•聚类。
1- Filter Bank
We present the channels with a bank of two-dimensional Gabor filters. A two-dimensional Gabor function consists of a sinusoidal plane wave of some frequency and orientation, modulated by a two-dimensional Gaussian [3]. The Gabor filter in the spatial domain is given by
我们使用一组二维Gabor滤波器来呈现通道。二维Gabor函数由一些频率和方向的正弦平面波组成，由二维高斯[3]调制。空间域中的Gabor滤波器由下式给出
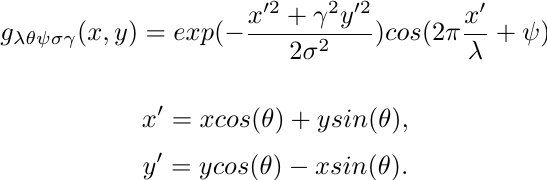
In this equation, λ represents the wavelength of the cosine factor, θ represents the orientation of the normal to the parallel stripes of a Gabor function in degrees, ψ is the phase offset in degrees, and γ is the spatial aspect ratio and specifies the elliptically of the support of the Gabor function, and σ is the standard deviation of the Gaussian determines the (linear) size of the receptive field.
在该等式中，λ表示余弦因子的波长，θ表示以度为单位的Gabor函数的平行条纹的法线方向，ψ是以度为单位的相位偏移，γ是空间宽高比并且指定椭圆形Gabor函数的支持，σ是高斯的标准偏差决定了感受野的（线性）大小。
The parameter λ is the wavelength and f = 1/λ is the spatial frequency of the cosine factor. The ratio σ/λ determines the spatial frequency bandwidth of simple cells and thus the number of parallel excitatory and inhibitory stripe zones which can be observed in their receptive fields. The half-response spatial frequency bandwidth b (in octaves) and the ratio σ/λ are related as follows:
参数λ是波长，f = 1 /λ是余弦因子的空间频率。比率σ/λ决定了简单细胞的空间频率带宽，从而确定了在其感受野中可以观察到的平行兴奋和抑制条带区域的数量。半响应空间频率带宽b（以八度为单位）和比率σ/λ如下相关：
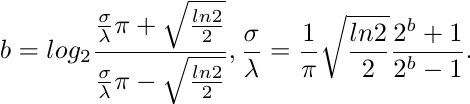
ψ = 0◦ and ψ = 90◦ returns the real part and the imaginary part of Gabor filter respectively. The real part of Gabor filter is an even-symmetric filter, and the property satisfies the requirement proposed by Malik [1]. Therefore, we use the real part of Gabor.
ψ= 0°和ψ= 90°分别返回Gabor滤波器的实部和虚部。Gabor滤波器的实部是偶对称滤波器，其性质满足Malik [1]提出的要求。因此，我们使用Gabor的真实部分。Choice of Filter Parameters
We use orientation separation angles of 30◦ as recommended in [4], that is:
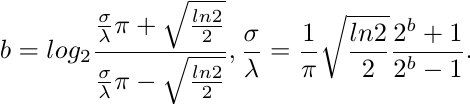
and following values of frequencies as recommended in [6]
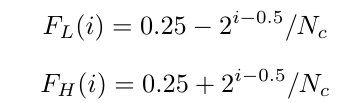
where 
, Nc is the width of image which is a power of 2. Note that 
and .
2- Feature Extraction
Jain [2] suggested to use a nonlinear sigmoidal function,
which saturates the output of the filters. Jain [2] also suggested to compute the average absolute deviation (AAD) for each filtered image. We use Gaussian smoothing function which is given by
它使滤波器的输出饱和。Jain [2]还建议计算每个滤波图像的平均绝对偏差（AAD）。我们使用由下式给出的高斯平滑函数
where σ is the standard deviation which determines the (linear) size of the receptive field (window size).
其中σ是确定感受野（窗口大小）的（线性）大小的标准偏差。
We choose 
where
is the scale parameter of Gabor filter given by (2) as similar to the recommendation, 
, by [6]
.3- Clustering
The final step is to cluster the pixels into a number of clusters representing the texture regions. Although Jain used CLUSTER algorithm [2], we use the k-means algorithm. The algorithm of k-means is as follows:
’ 1. Initialize centroids of K-clusters randomly.’
’ 2. Assign each sample to the nearest centroid.’
’ 3. Calculate centroids (means) of K-clusters.’
’ 4. If centroids are unchanged, done. Otherwise, go to step 2.’
Furthermore, we include the spatial coordinates of the pixels as two additional features to take into account the spatial adjacency information in the clustering process as proposed by [2].
最后一步是将像素聚类成表示纹理区域的多个聚类。虽然Jain使用CLUSTER算法[2]，但我们使用k-means算法。k-means的算法如下：
'1.随机初始化K-cluster的质心。
'2.将每个样本分配到最近的质心。
'3.计算K-cluster的质心（均值）。
'4.如果质心不变，那就完成了。否则，请转到步骤2。
此外，我们将像素的空间坐标作为两个附加特征包括在内，以考虑[2]中提出的聚类过程中的空间邻接信息。
4- Results
The multi-channel image segmentation system mentioned above was implemented and tested against a textured image from the Brodatz album [5]. The number of clusters is considered 5.
Also, the result is shown in another image as follow.
Bibliography
[1] Perona and Malik, ”Preattentive texture discrimination with early vision mechanisms,” J. Opt. Soc. Am. A, Vol. 7, No. 5, May 1990.
[2] A. K. Jain, F. Farrokhnia, ”Unsupervised texture segmentation using Gabor filters,” Pattern Recogni- tion, vol. 24, no. 12, pp.1167-1186, 1991.
[3] J.G. Daugman: ”Uncertainty relations for resolution in space, spatial frequency, and orientation opti- mized by two-dimensional visual cortical filters”, Journal of the Optical Society of America A, 1985, vol. 2, pp. 1160-1169.
[4] D. Clausi, M. Ed Jernigan, ”Designing Gabor filters for optimal texture separability,” Pattern Recogni- tion, vol. 33, pp. 1835-1849, 2000.
[5] P. Drodatz, ”Textures: A Photographic Album for Artists and Designers,” ”’Dover”’, New York, 1966.
[6] Jianguo Zhang, Tieniu Tan, Li Ma, ”Invariant texture segmentation via circular gabor filter”, Proceedings of the 16th IAPR International Conference on Pattern Recognition (ICPR), Vol II, pp. 901-904,2002.