2019寒假集训第五场（新生场）中石油补题和题解

这场比赛本来我都出去了，然后看到老师发消息又回来了= = 然后做着做着正好mhr大佬在外面有一些事情突然没法比赛，于是就帮他交了两道题看看对不对，便于之后补题，然后还真都对了，下面是题目和解析：

问题 A: 水题大战

题目描述

小Q最近正在给一个比赛出题目，他认为第一题应该是老少皆宜的。于是，他出了一个题目，然后让n个人来评价这个题目。
每个人会对这个题目做出评价，有难和简单两种，1表示难，0表示简单。如果所有人都认为这个题目简单，那么这个题目就是简单的，否则这个题目就是难的。

输入

输入第一行是一个正整数T，表示数据的组数。
接下来对于每组数据，先输入一个正整数n，表示参与评价的人的数量，接下来一行有n个整数，每个整数都是0或者1，表示对当前题目的评价。

输出

输出共T行，每行一个答案。如果该题简单，就输出EASY，否则输出HARD。

样例输入
复制样例数据 2
3
0 0 1
1
0

样例输出
HARD
EASY

提示

样例共有2组数据：
第一组数据n是3,2个人认为是简单，1个人认为是难，所以是HARD。
第二组数据n是1，这唯一的一个人认为是简单的，所以是EASY。

对于40%的数据，T=1,1≤n≤5。
对于100%的数据，1≤T≤10,1≤n≤100。

题如其名，是一道彻头彻尾的水题，只要拿一个开关判断是不是只有0就行了 代码：

#include
using namespace std;
int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  int t;
  cin>>t;
  while(t--)
  {
    int f=0;
    int n;
    cin>>n;
    int a;
    for(int i=0;i<n;i++)
    {
      cin>>a;
      if(a==1)
      f=1;
    }
    if(f)
    cout<<"HARD"<<"\n";
    else
    cout<<"EASY"<<"\n";
  }
}

问题 B: 学生分组

题目描述

在小Q的大学里，有n个学生，其中n一定是偶数。每个学生有一定的编程能力，第i个学生的能力是ai。
学校里的老师希望把学生组成n/2个队伍， 每个队伍里面有2个学生，每个学生只能属于一个队伍。两个学生可以组队，当且仅当他们的能力是相同的，否则他们就不能理解对方。
由于开始的时候， 学生的能力参差不齐，可能无法顺利组队。但是学生可以通过做题来提高自己的能力，每做一题，能力就可以提高1 。
学校的老师希望计算出这些学生最少需要做多少题，才能顺利的组队。

输入

输入的第一行是一个正整数n，表示学生的数量，保证n一定是偶数。
接下来一行有n个正整数，第i个整数ai表示第i个学生当前的编程能力。

输出

输出只有一行一个整数，表示所有学生最少需要做的总题数，才能使得顺利组队。

样例输入
复制样例数据 6
5 10 2 3 14 5

样例输出
5

提示

样例中，第3个人和第4个人组队，第1个人和第6个人组队，第2个人和第5个人组队，然后第3个人做1题，第2个人做4题，总共做5题，他们就能顺利组队了。

对于50%的数据，1≤n≤1000，所有学生的能力最多只有2种不同的取值。
对于100%的数据，1≤n≤100000，1≤ai≤100。

典型的贪心题目，要想得到两两之间的最小差和，只需要排序然后两两相减，这样两数之间的差就是最小的了 代码：

#include
using namespace std;
int a[100010];
int main()
{
  int n;
  cin>>n;
  for(int i=0;i<n;i++)
  cin>>a[i];
  sort(a,a+n);
  int ans=0;
  for(int i=0;i<n;i++)
  {
    if(i%2!=0)
    {
      ans+=a[i]-a[i-1];
    }
  }
  cout<<ans;
}

问题 C: 变换高度

题目描述

小Q是一个牛逼的少年，他段近无聊的在纸上画了n个塔.第i个塔的高度是hi。他会对塔进行一种操作，操作定义为在某个高度H的时候，如果第i个塔的高度高于H，我们必须把这个培的高度变成H. 这样一次操作的代价是从所有塔里面移除的1×1方块的总和。如果一次操作的代价小于等于k，那么我们就称这个操作为友好操作（k≥n）。
现在请你计算最少需要多少次友好操作，才能使得所有的塔的高度都变成相同。显然，这个肯定有答案．下面图可以参考（样例1 ) :

输入

输入第－行是两个整数n和k， 表示塔的数量和操作相关的系数k。
第二行有n个空格隔开的整数h1,h2,…hn。

输出

输出只有一个整数，表示最少需要的友好操作的数量，使得每个塔的高度都相同。

样例输入
复制样例数据 5 5
3 1 2 2 4

样例输出
2

提示

样例如图所示，需要2个友好操作，第1次设定H为2，代价为3，第2次设定H为1，代价为4。

对于50%的数据，1≤n≤2000，hi≤2000。
对于100%的数据，1≤n≤2×105，n≤k≤109，hi≤2×105

这道题看起来和中石油第一次的修建高楼挺像的，但是仔细一想还是有区别，这道题是mhr大佬在外面做的然后托我提交的，然后赛后我又打了一次换了一下格式，大体的思路是这样的：设置一个ans1数组，用来存取当前输入的高楼的高度的数量，就相当于记录了那个高度一层的数量，然后记录一下最大值和最小值，从最大值开始循环，相当于从最高的那层楼的高度开始循环，用sum加上当前高度的数量，如果数量小于k的话就说明h可以从这个地方往上截，但是这不一定是最优解，因为要找的是最少的截取次数，所以继续往下找，如果加上以后sum大于k，就从这一层开始取h，然后ans++，最后不要忘了把sum归零以后再加上之前加不上的这一层，如果这一层小于k的话就得再截取一次，ans++，如果大于的话就满足条件了，不用再加了

帮忙提交的代码：

#include 
using namespace std;
int bk[666666];
int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  int n,k,maxn=-1,minn=999999999,ans=0,sum=0;
  cin>>n>>k;
  for(int i=0;i<n;i++)
  {
    int t;
    cin>>t;
    maxn=max(maxn,t);
    minn=min(minn,t);
    bk[t]++;
  }
  for(int i=maxn;i>=minn;i--)
  {
    if(bk[i]==n)
    {
      if(sum)
      ans++;
      break;
    }
    if(sum+bk[i]<=k)
    sum+=bk[i];
    else
    {
      ans++;
      sum=0;
      if(sum+bk[i]<=k)
      sum+=bk[i];
    }
    bk[i-1]+=bk[i];
    bk[i]=0;
    //cout<
  }
  cout<<ans;
}
 

按着思路换了个形式的代码：

#include 
using namespace std;
int ans1[300000];
int sum;
int n;
int k;
int maxn=-9999999;
int minn=9999999;
int ans;
void init()
{
  cin>>n>>k;
}
void solve()
{
  for(int i=0;i<n;i++)
  {
    int num;
    cin>>num;
    maxn=max(maxn,num);
    minn=min(minn,num);
    ans1[num]++;
  }
  for(int i=maxn;i>=minn;i--)
  {
    if(ans1[i]==n)
    {
      if(sum)
      ans++;
      break;
    }
    if(sum+ans1[i]<=k)
    sum+=ans1[i];
    else
    {
      ans++;
      sum=0;
      if(sum+ans1[i]<=k)
      sum+=ans1[i];
    }
    ans1[i-1]+=ans1[i];
    ans1[i]=0;
  }
  cout<<ans;
}
int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  init();
  solve();
}

问题 D: 统计序列

题目描述

有一天， 小Q想起了一个统计公式， 定义一个长度为m的序列，我们可以得到V,V的计算如下：

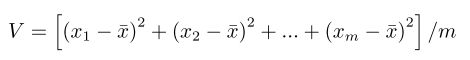
其中：

现在给你n个整数，需要从中选出m个数，使得他们构成的序列的V值最小。
为了方便，你只需要输出最小的V值乘以m2的值，可以证明这是一个整数。

输入

输入第一行两个正整数n和m。接下来n行，每行一个正整数，表示给你的n个数。

输出

输出一个整数表示答案，保证答案不超过int64.

样例输入
复制样例数据 5 3
1
2
3
4
5

样例输出
6

提示

比如选择了1,2,3这3个数，平均数是2，所以V值是，乘上m2后就变成了6。
对于20%的数据，1≤m≤n≤10。
对于50%的数据，1≤m≤n≤1000。
对于100%的数据，1≤m≤n≤100000，给定的n个数的范围是0到104。

此处无声胜有声（待解决2333）

问题 E: 统计字数

题目描述

大家都知道Word是一个强大的文字处理软件，具有丰富的字数统计功能。

小明听说你学习了程序设计，想请你帮他制作一个简易统计字数的软件，现在给定小明书写的一段文字，请你统计出文字中，英文字母数量，数字字符数量。

输入

第一行包含一个字符串包含英文字母和数字，以及一些常见标点符号，不包含中文。

输出

两个整数，中间用空格分隔，分别表示英文字母数量和数字字符数量。

样例输入
复制样例数据 2018YuyaoProgrammingContest.

样例输出
23 4

提示

对于60%的数据，这段文字中的长度不超过200。
对于100%的数据，文字长度不超过1000。
另有50%的数据，不包含空格字符。

emmm这题可以说是水题了把，注意输入的时候得输入一行，用getline(cin,a);，统计的时候注意一下用isalpha 和 isdigit函数就行了 代码：

#include
using namespace std;
int main()
{
  string a;
  getline(cin,a);
  int b=0;
  int c=0;
  for(int i=0;i<a.size();i++)
  {
    if(isalpha(a[i]))
    b++;
    else if(isdigit(a[i]))
    c++;
  }
  cout<<b<<" "<<c;
}

问题 F: 整数拆分

题目描述

小明最近在学习整数拆分，他在草稿纸上随手写下了一串数字，仅包含“0”~“9”这十种数字，长度不超过9。
现在你可以在这串数字中选出任意一个子串（不能为空，可以是原串），不能以数字“0”开始。小明想要知道，这些可能的子串构成的数，有多少个比他心目中的幸运数字x更大。
注：子串只要在原串中的起始或者终止位置不同，就认为是不同的子串；子串和x都是十进制的。

输入

第一行输入一个数字串S，仅包含数字“0”~“9”这十种数字，长度不超过9。
第二行包含一个整数x，表示小明的幸运数字。

输出

有多少个非“0”开始的子串，表示成十进制数后比x更大。

样例输入
复制样例数据 1023
12

样例输出
3

提示

子串“23”、“102”和子串“1023”，都要比12更大。

对于50%的数据，S的第一个字母不超过“2”。
对于100%的数据，S仅包含数字“0”~“9”这十种数字，1<=S的长度<=9；0<=x<=777444111。

这道题由于是连续的字串，所以直接暴力枚举就可以解决，用stringstream从string类型转化成long long int 类型，与输入的b比较一下，如果比他大答案加1就行了 代码：

#include 
using namespace std;
int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  string a;
  cin>>a;
  int b;
  long long sum=0;
  cin>>b;
  for(int i=0;i<a.size();i++)
  {
    string c="";
    if(a[i]=='0')
    continue;
    for(int j=i;j<a.size();j++)
    {
      c+=a[j];
      stringstream s;
      s<<c;
      long long ans;
      s>>ans;
      if(ans>b)
      sum++;
    }
  }
  cout<<sum;
}

问题 G: 真假鉴定

题目描述

有n堆硬币依次排列，每一堆有a_i个。每堆硬币全是真币或全是假币，真币每个重5克，假币每个重4克。你有一台电子天平，可以从每堆硬币中挑出若干个进行一次称量（也可以一个都不选）。现在你想要知道，若要确定前1,2,……,n堆硬币的真假，至少要称量几次。

输入

第一行一个整数n，表示硬币的堆数。
接下来一行n个整数a_i，表示每堆硬币的数量。

输出

n行，每行一个整数，第i行表示想要确定前i堆硬币的真假至少要称量几次。

样例输入
复制样例数据 3
2 3 4

样例输出
1
1
1

提示

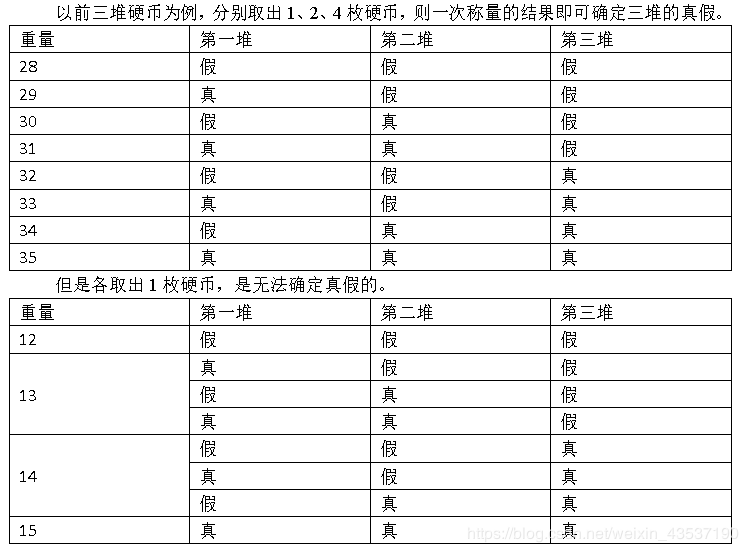
对于10%的数据，n≤1
对于30%的数据，n≤2
对于60%的数据，n≤100
对于80%的数据，n≤1000
对于100%的数据，n≤10^5，a_i≤109
存在10%的数据，a_i=1

这题也是mhr大佬让我帮忙交的，说是随便水一下没想到直接对了，只能说太强了。按图索骥的话思路是这样的：只要满足每次能从钱堆里拿出来的钱数量不一样就能判断，如果不能判断的话需要ans++多判断一次，达到钱数不相等的条件最简单的实现就是让sum每次加一，于是就有了以下代码，但是感觉有点贪心的意思2333 ：

#include 
using namespace std;
int num[666666];
int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0);
  cout.tie(0);
  int n,sum=1,ans=1;
  cin>>n;
  for(int i=0;i<n;i++)
  cin>>num[i];
  for(int i=0;i<n;i++)
  {
    if(num[i]>=sum)
    cout<<ans<<"\n",sum++;
    else
    {
      ans++;
      cout<<ans<<"\n";
    }
  }
}

问题 H: 最大公约数

题目描述

给定n个正整数，a_1,a_2,…,a_n,求最少删去几个数，使得删去后这些数的最大公约数比原先的所有数的最大公约数大。

输入

第一行一个整数n，第二行n个正整数，a_1,a_2,…,a_n。

输出

一个数，表示最少删去的个数，若无论怎么删都不会比原来的大，输出-1。

样例输入
复制样例数据 3
1 2 4

样例输出
1

提示

删去1这个数，最大公约数从1变到2。
对于30%的数据，n<=15
对于50%的数据，n,a_i<=1000
对于100%的数据，n<=300,000，a_i<=1.5*10^7

此处无声胜有声（待解决2333）

总结：第一题那么水看完题目就开始疯狂写没想到还是没有抢到一血。。看来水题还得加快码速啊！