数据结构精录&总结Episode.8 数据结构入门之查找（基于Visual C++）

最近两天魅族17手机发布，罗永浩老师又要开始直播带货了。但是一改往日的自信，罗永浩老师对于本次魅族17发布会的态度不甚悲观。其中他在微博上的回复提到，魅族17发布会看不看都无所谓，因为首先是可以看回放，其次是大家口头支持一波实际上还是都买Iphone去了。

有点酸，但是支持国货当然更不应该停留在言论上。2020Q1季度的财报显示，手机成交额/成交量仍然是Iphone11占领头衔，除次以外小米Redmi系列勉强上榜，诸如华为等国内一众呼声很高的企业连影子都没有。

再过两天博主也决定要将自己的Iphone更换成华为P40 Pro了，不管曾经这些公司怎么样，做了什么，支持国货总是有利无弊的。尤其是在当前疫情期间国际经济等等形势都不景气的情况下。

---

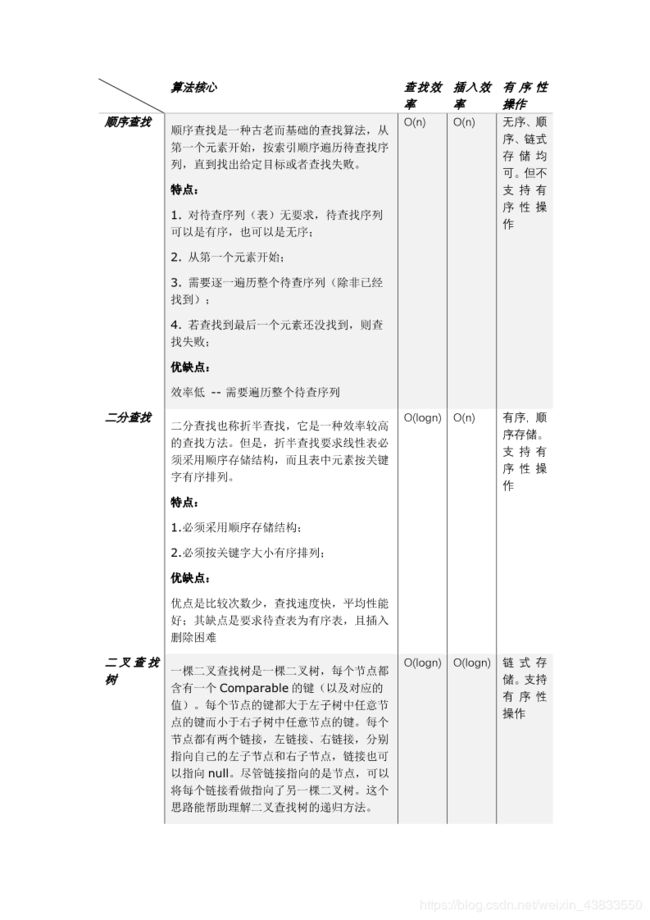
查找算法，总结起来分为线性表查找、树表查找和散列表查找三大类，其中线性表查找分为顺序查找和折半查找，树表查找分为二叉查找树与平衡二叉查找树。实际上树表查找中还有许许多多的子分支如红黑树，这些对于非计算机专业的同学来说仅需了解，故次从略。以下是博主自行编写的的查找算法总结表。

---

上述总结对应的代码如下，具体解释等已嵌入注释中。

// 第八章 查找.cpp : 此文件不包含 "main" 函数。程序执行将分别在下述的各个cpp中。编写—JoeyBG，算法尚有不足之处，敬请谅解。
//

/*
#include 
#include
#include
#include
using namespace std;
*/

// 运行程序: Ctrl + F5 或调试 >“开始执行(不调试)”菜单
// 调试程序: F5 或调试 >“开始调试”菜单
// 入门使用技巧: 
//   1. 使用解决方案资源管理器窗口添加/管理文件
//   2. 使用团队资源管理器窗口连接到源代码管理
//   3. 使用输出窗口查看生成输出和其他消息
//   4. 使用错误列表窗口查看错误
//   5. 转到“项目”>“添加新项”以创建新的代码文件，或转到“项目”>“添加现有项”以将现有代码文件添加到项目
//   6. 将来，若要再次打开此项目，请转到“文件”>“打开”>“项目”并选择 .sln 文件

//顺序查找
#include
using namespace std;
#define Maxsize 100

int SqSearch(int r[],int n,int x)//顺序查找
{
	for(int i=0;i>n;
    cout<<"请依次n个元素："<>r[i];
        r2[i+1]=r[i];//r2[]数组0空间未用，做监视哨
    }
    cout<>x;
    //i=SqSearch(r,n,x);
//    if(i==-1)
//      cout<<"该数列中没有要查找的元素"<

//折半查找
#include
#include //排序sort函数需要该头文件
#include
using namespace std;
const int M=100;
int x,n,i;
int s[M];

int BinarySearch(int s[],int n,int x)//二分查找非递归算法
{
   int low=0,high=n-1;  //low指向有序数组的第一个元素，high指向有序数组的最后一个元素
   while(low<=high)
   {
       int middle=(low+high)/2;  //middle为查找范围的中间值
       if(x==s[middle])  //x等于查找范围的中间值，算法结束
          return middle;
       else if(x>s[middle]) //x大于查找范围的中间元素，则从左半部分查找
              low=middle+1;
            else            //x小于查找范围的中间元素，则从右半部分查找
              high=middle-1;
    }
    return -1;
}

int recursionBS (int s[],int x,int low,int high) //二分查找递归算法
{
    //low指向数组的第一个元素，high指向数组的最后一个元素
    if(low>high)              //递归结束条件
        return -1;
    int middle=(low+high)/2;  //计算middle值(查找范围的中间值)
    if(x==s[middle])          //x等于s[middle]，查找成功，算法结束
        return middle;
    else if(x>n;
    cout<<"请依次输入数列中的元素：";
    for(i=0;i>s[i];
    sort(s,s+n); //二分查找的序列必须是有序的，如果无序需要先排序
    cout<<"排序后的数组为：";
    for(i=0;i>x;
    //i=BinarySearch(s,n,x);
    i=recursionBS(s,x,0,n-1);
    if(i==-1)
		cout<<"该数列中没有要查找的元素"<

//二叉查找树
#include
using namespace std;
#define ENDFLAG -1
typedef int ElemType;

typedef struct BSTNode{
	ElemType data;	//结点数据域
	BSTNode *lchild,*rchild;	//左右孩子指针
}BSTNode,*BSTree;

BSTree SearchBST(BSTree T,ElemType key)//二叉排序树的递归查找
{
    //若查找成功，则返回指向该数据元素结点的指针，否则返回空指针
    if((!T)|| key==T->data)
        return T;
    else if (keydata)
            return SearchBST(T->lchild,key);//在左子树中继续查找
        else
            return SearchBST(T->rchild,key); //在右子树中继续查找
}

void InsertBST(BSTree &T,ElemType e)//二叉排序树的插入
{
    //当二叉排序树T中不存在关键字等于e的数据元素时，则插入该元素
    if(!T)
    {
        BSTree S=new BSTNode; //生成新结点
        S->data=e;             //新结点S的数据域置为e
        S->lchild=S->rchild=NULL;//新结点S作为叶子结点
        T=S;            		//把新结点S链接到已找到的插入位置
    }
    else if(edata)
            InsertBST(T->lchild,e );//插入左子树
        else if(e>T->data)
            InsertBST(T->rchild,e);//插入右子树
}

void CreateBST(BSTree &T )//二叉排序树的创建
{
    //依次读入一个关键字为key的结点，将此结点插入二叉排序树T中
    T=NULL;
    ElemType e;
    cin>>e;
    while(e!=ENDFLAG)//ENDFLAG为自定义常量，作为输入结束标志
    {
        InsertBST(T,e);  //插入二叉排序树T中
        cin>>e;
    }
}

void DeleteBST(BSTree &T,char key)
{
  //从二叉排序树T中删除关键字等于key的结点
    BSTree p=T;BSTree f=NULL;
    BSTree q;
    BSTree s;
    if(!T) return; //树为空则返回
    while(p)//查找
    {
        if(p->data==key) break;  //找到关键字等于key的结点p，结束循环
        f=p;                //f为p的双亲
        if (p->data>key)
            p=p->lchild; //在p的左子树中继续查找
        else
            p=p->rchild; //在p的右子树中继续查找
    }
    if(!p) return; //找不到被删结点则返回
    //三种情况：p左右子树均不空、无右子树、无左子树
    if((p->lchild)&&(p->rchild))//被删结点p左右子树均不空
    {
        q=p;
        s=p->lchild;
        while(s->rchild)//在p的左子树中继续查找其前驱结点，即最右下结点
        {
            q=s;
            s=s->rchild;
        }
        p->data=s->data;  //s的值赋值给被删结点p,然后删除s结点
        if(q!=p)
            q->rchild=s->lchild; //重接q的右子树
        else
            q->lchild=s->lchild; //重接q的左子树
        delete s;
    }
    else
    {
        if(!p->rchild)//被删结点p无右子树，只需重接其左子树
        {
            q=p;
            p=p->lchild;
        }
        else if(!p->lchild)//被删结点p无左子树，只需重接其右子树
        {
             q=p;
             p=p->rchild;
        }
        /*――――――――――将p所指的子树挂接到其双亲结点f相应的位置――――――――*/
        if(!f)
            T=p;  //被删结点为根结点
        else if(q==f->lchild)
                f->lchild=p; //挂接到f的左子树位置
            else
                f->rchild=p;//挂接到f的右子树位置
        delete q;
	}
}

void InOrderTraverse(BSTree &T)//中序遍历
{
    if(T)
	{
        InOrderTraverse(T->lchild);
        cout<data<<"\t";
        InOrderTraverse(T->rchild);
	}
}

int main()
{
	BSTree T;
	cout<<"请输入一些整型数，-1结束"<>key;
	BSTree result=SearchBST(T,key);
	if(result)
        cout<<"找到"<>key;
	DeleteBST(T,key);
	cout<<"当前有序二叉树中序遍历结果为"<

//平衡二叉查找树
#include
#include
#include
using namespace std;

typedef struct AVLNode{
   int data;
   int height;
   struct AVLNode *lchild;
   struct AVLNode *rchild;
}*AVLTree;

AVLTree Empty(AVLTree &T)//删除树
{
    if(T==NULL) return NULL;
    Empty(T->lchild);
    Empty(T->rchild);
    delete T;
    return NULL;
}

inline int Height(AVLTree T)//计算高度
{
    if(T==NULL) return 0;
    return T->height;
}

void updateHeight(AVLTree &T)
{
     T->height=max(Height(T->lchild),Height(T->rchild))+1;
}

AVLTree LL_Rotation(AVLTree &T)//LL旋转
{
    AVLTree temp=T->lchild;
    T->lchild=temp->rchild;
    temp->rchild=T;
    updateHeight(T);//更新高度
    updateHeight(temp);
    return temp;
}

AVLTree RR_Rotation(AVLTree &T)//RR旋转
{
    AVLTree temp=T->rchild;
    T->rchild=temp->lchild;
    temp->lchild=T;
    updateHeight(T);//更新高度
    updateHeight(temp);
    return temp;
}

AVLTree LR_Rotation(AVLTree &T)//LR旋转
{
     T->lchild=RR_Rotation(T->lchild);
     return LL_Rotation(T);
}

AVLTree RL_Rotation(AVLTree &T)//RL旋转
{
    T->rchild=LL_Rotation(T->rchild);
    return RR_Rotation(T);
}

AVLTree Insert(AVLTree &T,int x)
{
    if(T==NULL) //如果为空，创建新结点
    {
        T=new AVLNode;
        T->lchild=T->rchild=NULL;
        T->data=x;
        T->height=1;
        return T;
     }
    if(T->data==x) return T;//查找成功，什么也不做，查找失败时才插入
    if(xdata)//插入到左子树
    {
        T->lchild=Insert(T->lchild,x);//注意插入后饭后结果挂接到T->lchild
        if(Height(T->lchild)-Height(T->rchild)==2)//插入后看是否平衡，如果不平衡显然是插入的那一边高度大
        {                                         //沿着高度大的那条路径判断
            if(xlchild->data)//判断是LL还是LR,即插入的是lchild节点的lchild 还是rchild
                T=LL_Rotation(T);
            else
                T=LR_Rotation(T);
        }
    }
    else//插入到右子树
    {
        T->rchild=Insert(T->rchild,x);
        if(Height(T->rchild)-Height(T->lchild)==2)
        {
            if(x>T->rchild->data)
                T=RR_Rotation(T);
            else
                T=RL_Rotation(T);
        }
    }
    updateHeight(T);
    return T;
}

AVLTree adjust(AVLTree &T)//删除结点后，需要判断是否还是平衡，如果不平衡，就要调整
{
    if(T==NULL) return NULL;
    if(Height(T->lchild)-Height(T->rchild)==2)//沿着高度大的那条路径判断
    {
        if(Height(T->lchild->lchild)>=Height(T->lchild->rchild))
            T=LL_Rotation(T);
        else
            T=LR_Rotation(T);
    }
    if(Height(T->rchild)-Height(T->lchild)==2)//沿着高度大的那条路径判断
    {
        if(Height(T->rchild->rchild)>=Height(T->rchild->lchild))
            T=RR_Rotation(T);
        else
            T=RL_Rotation(T);
    }
    updateHeight(T);
    return T;
}

AVLTree Delete(AVLTree &T,int x)
{
    if(T==NULL) return NULL;
    if(T->data==x)//如果找到删除节点
    {
        if(T->rchild==NULL)//如果该节点的右孩子为NULL,那么直接删除
        {
            AVLTree temp=T;
            T=T->lchild;
            delete temp;
        }
        else//否则，将其右子树的最左孩子作为这个节点，并且递归删除这个节点的值
        {
           AVLTree temp;
           temp=T->rchild;
           while(temp->lchild)
              temp=temp->lchild;
           T->data=temp->data;
           T->rchild=Delete(T->rchild,T->data);
           updateHeight(T);
        }
        return T;
    }

    if(T->data>x)//调节删除节点后可能涉及的节点
        T->lchild=Delete(T->lchild,x);
    if(T->datarchild=Delete(T->rchild,x);
    updateHeight(T);
	T=adjust(T);
    return T;
}

void Preorder(AVLTree T)//前序遍历方便看树的结果
{
    if(T==NULL) return ;
    cout<data<<"\t"<height<lchild);
    Preorder(T->rchild);
}

 void Inorder(AVLTree T)//中序遍历方便看树的结果
{
    if(T==NULL) return ;
    Inorder(T->lchild);
    cout<data<<"\t"<height<rchild);
}

 void Posorder(AVLTree T)//后序遍历方便看树的结果
{
    if(T==NULL) return ;
    Posorder(T->lchild);
    Posorder(T->rchild);
    cout<data<<"\t"<height<>n;
    for(int i=0;i>x;
        T=Insert(T,x);
    }
    return T;
}
int main()
{
    int x;
    AVLTree root=NULL;
    root=Empty(root);
    CreateAVL(root);
    show(root);
    cin>>x;
    root=Delete(root,x);
    show(root);
    return 0;
}

//散列表
#include
#include
#include
using namespace std;

#define m 15//哈希表的表长
#define NULLKEY 0//单元为空的标记

int HT[m],HC[m];

int H(int key)//哈希函数
{
	return key%13;
}

int Linedetect(int HT[],int H0,int key,int &cnt)
{
    int Hi;
    for(int i=1;i>x;//14 36 42 38 40 15 19 12 51 65 34 25
		if(!InsertHash(HT,x))
		{
		    cout<<"创建哈希表失败！"<>x;
	int result=SearchHash(HT,x);
	if(result!=-1)
		cout<<"在第"<

/*
参考资料：
1、陈小玉：趣学数据结构，人民邮电出版社，2019.09
*/

---

由于查找章节北理乐学平台是没有给出具体的代码练习题的，仅有知识点考核的选择题，在仔细阅读了上述总结的概念和代码后，正确回答它们不难，此略。