数据结构复习之简答题
（1）设待排序的关键字序列为{12，2，16，30，28，10，16*，20，6，18}，试分别写出使用以下排序方法，每趟排序结束后关键字序列的状态。
① 直接插入排序
② 折半插入排序
③ 希尔排序（增量选取5，3，1）
④ 冒泡排序
⑤ 快速排序
⑥ 简单选择排序
⑦ 堆排序
⑧ 二路归并排序
①直接插入排序
② 折半插入排序
折半插入排序在直接插入排序的基础上，在查询插入位置的时候采用的是折半查找，所以平均所需的查找比较的时间复杂度要更小，但是排序的过程和直接插入一样。
② 折半插入排序 排序过程同①
③ 希尔排序（增量选取5，3，1）
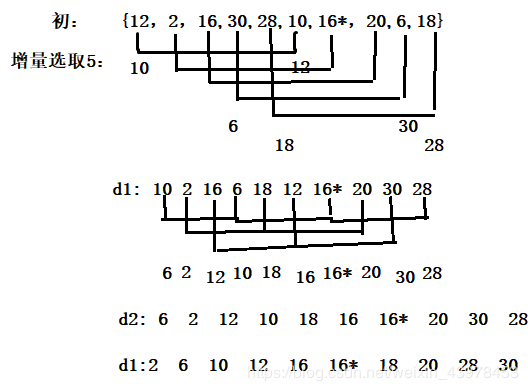④ 冒泡排序
⑤ 快速排序
12 [6 2 10] 12 [28 30 16* 20 16 18]
6 [2] 6 [10] 12 [28 30 16* 20 16 18 ]
28 2 6 10 12 [18 16 16* 20 ] 28 [30 ]
18 2 6 10 12 [16* 16] 18 [20] 28 30
16* 2 6 10 12 16* [16] 18 20 28 30
左子序列递归深度为1，右子序列递归深度为3
⑥ 简单选择排序
将最小的选出来放在前面
2 [12 16 30 28 10 16* 20 6 18]
2 6 [16 30 28 10 16* 20 12 18]
2 6 10 [30 28 16 16* 20 12 18]
2 6 10 12 [28 16 16* 20 30 18]
2 6 10 12 16 [28 16* 20 30 18]
2 6 10 12 16 16* [28 20 30 18]
2 6 10 12 16 16* 18 [20 30 28]
2 6 10 12 16 16* 18 20 [28 30]
2 6 10 12 16 16* 18 20 28 [30]
⑧ 二路归并排序
[2 12] [16 30] [10 28] [16 * 20] [6 18]
[2 12 16 30] [10 16* 20 28] [ 6 18 ]
[2 10 12 16 16* 20 28 30] [6 18]
2 6 10 12 16 16* 18 20 28 30
（2）假定对有序表：（3，4，5，7，24，30，42，54，63，72，87，95）进行折半查找，试回答下列问题：
① 画出描述折半查找过程的判定树；
② 若查找元素54，需依次与哪些元素比较？
③ 若查找元素90，需依次与哪些元素比较？
④ 假定每个元素的查找概率相等，求查找成功时的平均查找长度。
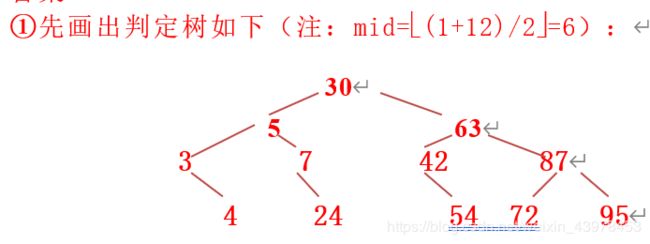②查找元素54，需依次与30, 63, 42, 54 元素比较；
③查找元素90，需依次与30, 63,87, 95元素比较
查找成功的平均查找长度为：
A S L = 1 12 ( 1 ∗ 1 + 2 ∗ 2 + 3 ∗ 4 + 4 ∗ 5 ) = 37 12 ASL=\frac{1}{12}(1*1+2*2+3*4+4*5)=\frac{37}{12} ASL=121(1∗1+2∗2+3∗4+4∗5)=1237
(3)在一棵空的二叉排序树中依次插入关键字序列为12，7，17，11，16，2，13，9，21，4，请画出所得到的二叉排序树。
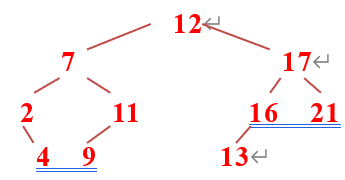
验算方法： 用中序遍历应得到排序结果：2,4,7,9,11,12,13,16,17,21
（4）设哈希表的地址范围为0～17，哈希函数为：H（key）=key%16。用线性探测法处理冲突，输入关键字序列：（10，24，32，17，31，30，46，47，40，63，49），构造哈希表，试回答下列问题：
① 画出哈希表的示意图；
② 若查找关键字63，需要依次与哪些关键字进行比较？
③ 若查找关键字60，需要依次与哪些关键字比较？
④ 假定每个关键字的查找概率相等，求查找成功时的平均查找长度。
②查找63,首先要与H(63)=63%16=15号单元内容比较，即63与31比较 ,不匹配;
然后顺移，与46,47,32,17,63相比，一共比较了6次！
③查找60,首先要与H(60)=60%16=12号单元内容比较，但因为12号单元为空（应当有空标记），所以应当只比较这一次即可。
ASL=1/11（6＋2＋3×3+6）＝23/11
（5）设哈希函数H（K）=3 K mod 11，哈希地址空间为0～10，对关键字序列（32，13，49，24，38，21，4，12），按下述两种解决冲突的方法构造哈希表，并分别求出等概率下查找成功时和查找失败时的平均查找长度ASLsucc和ASLunsucc。
① 线性探测法；
② 链地址法。
①：
ASLsucc =（1+1+1+2+1+2+1+2）/8=11/8
ASLunsucc=（1+2+1+8+7+6+5+4+3+2+1）/11=40/11
②：
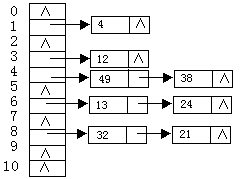
ASLsucc =（15+23）/8=11/8
ASLunsucc=（1+2+1+2+3+1+3+1+3+1+1）/11=19/11
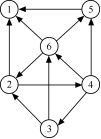
（6）已知图6.32所示的有向图，请给出：
① 每个顶点的入度和出度；
② 邻接矩阵；
③ 邻接表；
④ 逆邻接表。
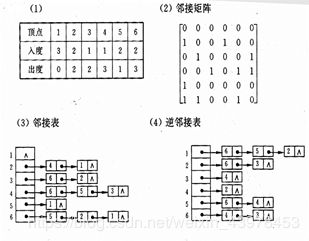
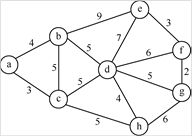
（7）已知如图6.33所示的无向网，请给出：
① 邻接矩阵；
② 邻接表；
③ 最小生成树
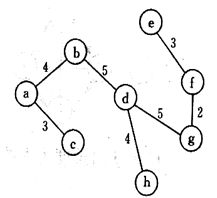
答案：省略邻接矩阵和邻接表
最小生成树：
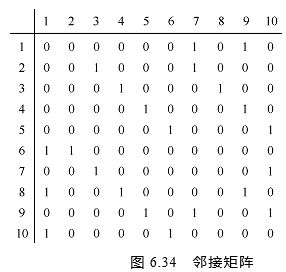
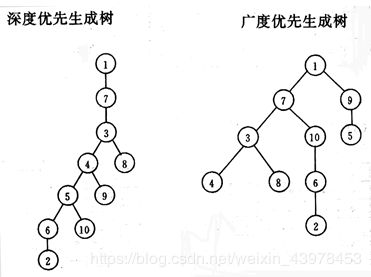
（8）已知图的邻接矩阵如图6.34所示。试分别画出自顶点1出发进行遍历所得的深度优先生成树和广度优先生成树。
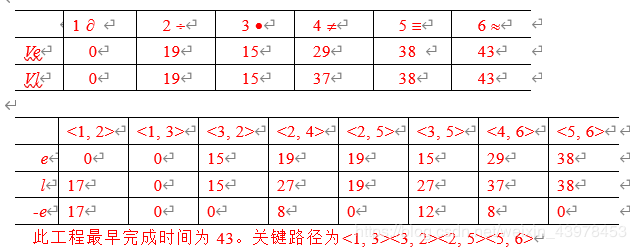
（9）试对图6.36所示的AOE-网：
① 求这个工程最早可能在什么时间结束；
② 求每个活动的最早开始时间和最迟开始时间；
③ 确定哪些活动是关键活动
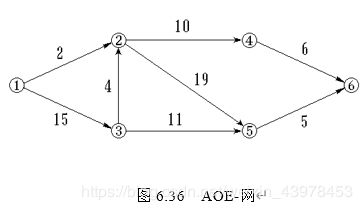
按拓扑有序的顺序计算各个顶点的最早可能开始时间Ve和最迟允许开始时间Vl。然后再计算各个活动的最早可能开始时间e和最迟允许开始时间l，根据l - e = 0? 来确定关键活动，从而确定关键路径。
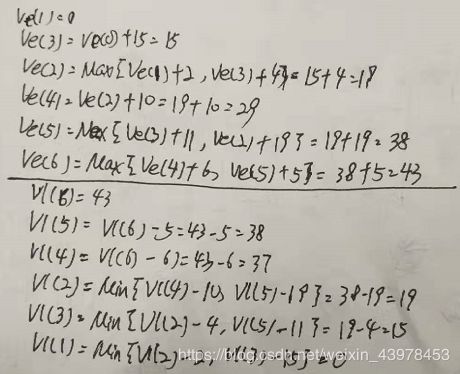
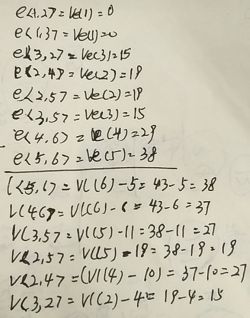
（10）试找出满足下列条件的二叉树
① 先序序列与后序序列相同 ②中序序列与后序序列相同
③ 先序序列与中序序列相同 ④中序序列与层次遍历序列相同
答案：
① 或为空树，或为只有根结点的二叉树
② 或为空树，或为任一结点至多只有左子树的二叉树．
③ 或为空树，或为任一结点至多只有右子树的二叉树．
④ 或为空树，或为任一结点至多只有右子树的二叉树
（11）设一棵二叉树的先序序列： A B D F C E G H ，中序序列： B F D A G E H C
①画出这棵二叉树。
②画出这棵二叉树的后序线索树。
③将这棵二叉树转换成对应的树（或森林）。
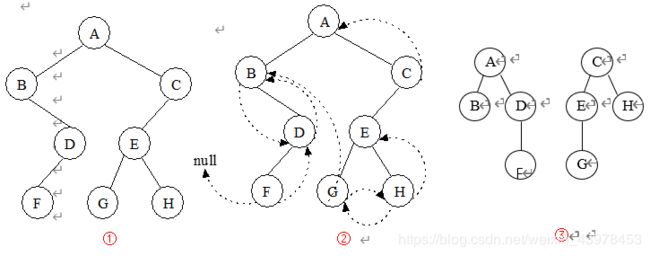
注意：树转换成二叉树的规则是左子树指向自己的孩子，右子树指向自己的兄弟
（12）假设用于通信的电文仅由8个字母组成，字母在电文中出现的频率分别为0.07，0.19，0.02，0.06，0.32，0.03，0.21，0.10。
① 试为这8个字母设计赫夫曼编码。
② 试设计另一种由二进制表示的等长编码方案。
③ 对于上述实例，比较两种方案的优缺点。
答案：方案1；哈夫曼编码
先将概率放大100倍，以方便构造哈夫曼树。
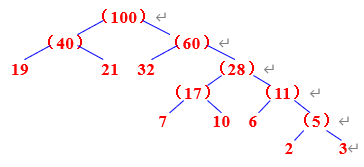
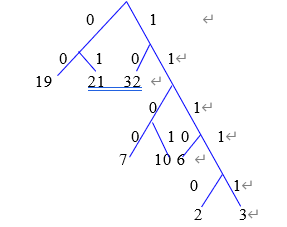
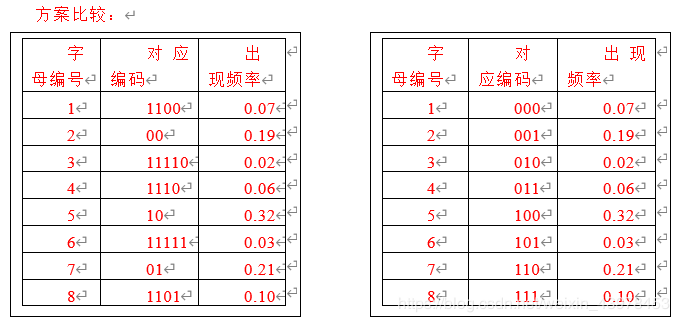方案1的WPL＝2(0.19+0.32+0.21)+4(0.07+0.06+0.10)+5(0.02+0.03)=1.44+0.92+0.25=2.61
方案2的WPL＝3(0.19+0.32+0.21+0.07+0.06+0.10+0.02+0.03)=3
结论：哈夫曼编码优于等长二进制编码
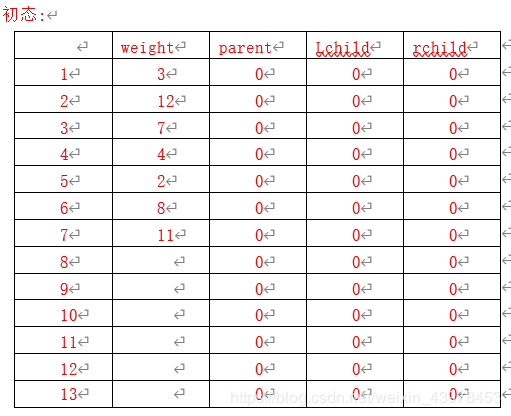
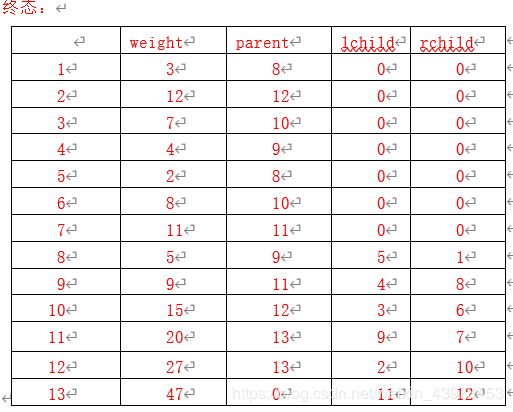
（13）已知下列字符A、B、C、D、E、F、G的权值分别为3、12、7、4、2、8，11，试填写出其对应哈夫曼树HT的存储结构的初态和终态。
（14）数组A中，每个元素A[i,j]的长度均为32个二进位,行下标从-1到9，列下标从1到11，从首地址S开始连续存放主存储器中，主存储器字长为16位。求：
① 存放该数组所需多少单元？
② 存放数组第4列所有元素至少需多少单元？
③ 数组按行存放时，元素A[7,4]的起始地址是多少？
④ 数组按列存放时，元素A[4,7]的起始地址是多少？
答案：每个元素32个二进制位，主存字长16位，故每个元素占2个字长，行下标可平移至1到11。
（1） 11 ∗ 11 ∗ 2 = 242 11*11*2=242 11∗11∗2=242
（2）11*2=22
（3）s+182 （4）s+142