八十四、Python | Leetcode回溯算法系列

@Author：Runsen
@Date：2020/7/7

人生最重要的不是所站的位置，而是内心所朝的方向。只要我在每篇博文中写得自己体会，修炼身心；在每天的不断重复学习中，耐住寂寞，练就真功，不畏艰难，奋勇前行，不忘初心，砥砺前行，人生定会有所收获，不留遗憾 （作者：Runsen ）

作者介绍：Runsen目前大三下学期，专业化学工程与工艺，大学沉迷日语，Python， Java和一系列数据分析软件。导致翘课严重，专业排名中下。.在大学60%的时间，都在CSDN。决定今天比昨天要更加努力。

前面文章，点击下面链接

我的Python教程，不断整理，反复学习

今天高考，当年我就是一个辣鸡，现在还是一个辣鸡，祝高考的个个清华北大
。辣鸡的我决定继续更新Python教程，今天就开始了八十四、Python | Leetcode回溯算法系列。

回溯算法

回溯算法(Backtracking Algorithm)，实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。(上述定义来自百度百科)

基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。

八皇后问题就是回溯算法的典型

假设有一个8X8的棋盘，要放8个棋子（皇后）每个棋子所在行，列，对角线不能有棋子

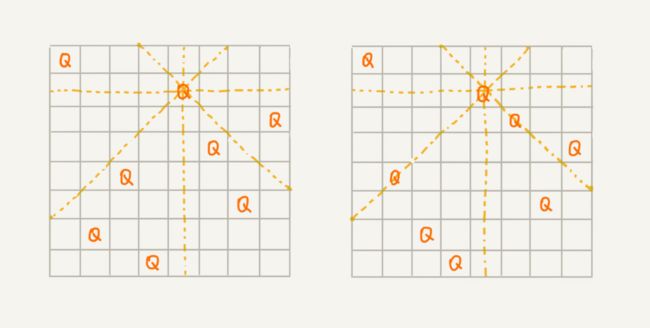
第一步按照第一行放一个皇后，然后第二行符合要求放第2个皇后，如果没有位置符合要求，那么就要改变第一个皇后的位置，重新放第2个皇后的位置，直到找到符合条件的位置就可以了。

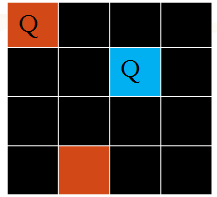
我们首先将问题简化为四皇后问题，并用回溯法来找到他们的解。目的是在4x4的棋盘上，使得4个皇后不能在同行同列以及同斜线上。

首先尝试将皇后放入第一个格子，被涂黑的地方是不能放皇后

第二行的皇后只能放在第三格或第四格，比方我们放第三格，则：

可以看到再难以放下第三个皇后，此时我们就要用到回溯算法了。我们把第二个皇后更改位置，此时我们能放下第三枚皇后了。

虽然是能放置第三个皇后，但是第四个皇后又无路可走了。返回上层调用（3号皇后），而3号也别无可去，继续回溯上层调用（2号），2号已然无路可去，继续回溯上层（1号），于是1号皇后改变位置如下，继续回溯。

上述就是回溯算法的过程，根据这个算法，最终能够把四位皇后放在4x4的棋盘里。也能用同样的方法解决了八皇后问题甚至N皇后问题。

Leetcode第51题，面试题 08.12：八皇后

#设计一种算法，打印 N 皇后在 N × N 棋盘上的各种摆法，其中每个皇后都不同行、不同列，也不在对角线上。这里的“对角线”指的是所有的对角线，不只是平分整个棋盘的那两条对角线。 
# 注意：本题相对原题做了扩展 
# 示例: 
#  输入：4
# 输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
# 解释: 4 皇后问题存在如下两个不同的解法。
#[
# [".Q..",  // 解法 1
#  "...Q",
#  "Q...",
#  "..Q."],
#
# ["..Q.",  // 解法 2
#  "Q...",
#  "...Q",
#  ".Q.."]
#]
# 
# Related Topics 回溯算法

在此之前写过练习、Python的八皇后（四十），因此不写题解，具体代码如下。

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        res = []
        s = "." * n
        def backtrack(i, tmp,col,z_diagonal,f_diagonal):
            if i == n:
                res.append(tmp)
                return 
            for j in range(n):
                if j not in col and i + j not in  z_diagonal and i - j not in f_diagonal:
                    backtrack(i+1,tmp + [s[:j] + "Q" + s[j+1:]], col | {j}, z_diagonal |{i + j} , f_diagonal |{i - j}  ) 
            
        backtrack(0,[],set(),set(),set())    
        return res

Leetcode第46题，全排列

#给定一个 没有重复 数字的序列，返回其所有可能的全排列。 
# 示例: 
# 输入: [1,2,3]
#输出:
#[
#  [1,2,3],
#  [1,3,2],
#  [2,1,3],
#  [2,3,1],
#  [3,1,2],
#  [3,2,1]
#] 
# Related Topics 回溯算法

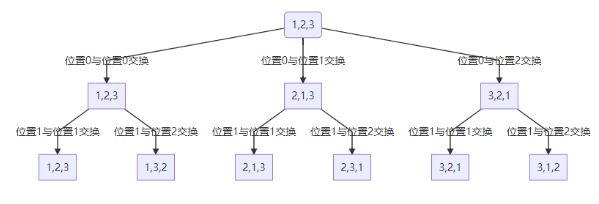
具体来说，假设我们已经填到第index个位置，那么nums[] 数组中[0, index - 1]是已填过的数的集合，[index - 1, length - 1] 是待填的数的集合。我们肯定是尝试用[0, index - 1]里的数去填第index个数，假设待填的数的下标为i，那么填完以后我们将第i个数和第index个数交换，即能使得在填第index + 1个数的时候nums[] 数组的[0, index]部分为已填过的数，[index + 1, n - 1]为待填的数，回溯的时候交换回来即能完成撤销操作。

具体来说，假设我们已经填到第index个位置，那么nums[] 数组中[0, index - 1]是已填过的数的集合，[index - 1, length - 1] 是待填的数的集合。我们肯定是尝试用[0, index - 1]里的数去填第index个数，假设待填的数的下标为i，那么填完以后我们将第i个数和第index个数交换，即能使得在填第index + 1个数的时候nums[] 数组的[0, index]部分为已填过的数，[index + 1, n - 1]为待填的数，回溯的时候交换回来即能完成撤销操作。

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        """itertools库内置了这个函数"""
        return itertools.permutations(nums)
    
    def permute2(self, nums: List[int]) -> List[List[int]]:
        """自己写回溯法"""
        res = []
        def _backtrace(nums, pre_list):
            if len(nums) <= 0:
                res.append(pre_list)
            else:
                for i in nums:
                    # 注意copy一份新的调用，否则无法正常循环
                    p_list = pre_list.copy()
                    p_list.append(i)
                    left_nums = nums.copy()
                    left_nums.remove(i)
                    _backtrace(left_nums, p_list)
        _backtrace(nums, [])
        return res

class Solution:
    def __init__(self):
        self.res = []

    def permute(self, nums: List[int]) -> List[List[int]]:
        self.back_trace(nums, [])
        return self.res

    def back_trace(self, nums, tmp):
        if not nums:
            self.res.append(tmp)
        else:
            for i in range(len(nums)):
                self.back_trace(nums[:i] + nums[i + 1:], tmp + [nums[i]])

Leetcode第39题，组合总和

#给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 
# candidates 中的数字可以无限制重复被选取。 
# 说明： 
# 所有数字（包括 target）都是正整数。 
# 解集不能包含重复的组合。 
# 示例 1: 
# 输入: candidates = [2,3,6,7], target = 7,
#所求解集为:
#[
#  [7],
#  [2,2,3]
#]
# 示例 2: 
# 输入: candidates = [2,3,5], target = 8,
#所求解集为:
#[
#  [2,2,2,2],
#  [2,3,3],
#  [3,5]
#] 
# Related Topics 数组 回溯算法

首先对candidates排序

若candidates为空，则返回[]

回溯函数helper()，传入参数：下一加和索引i，当前已加和数组tmp，下一目标target

若target==0，说明当前和满足条件，将当前加和数组tmp加入res，并return。

因为已经将candidates排序，所以当下一目标小于下一待加和数时，return。

并且当下一待加和索引i==n时，return。为了防止数组越界，将条件i==n放在target

因为可重复调用元素，所以helper(i,tmp+[candidates[i],target-candidates[i]]继续重复调用自身。

调用数组中下一元素，寻找新答案。helper(i+1,tmp,target])。执行helper(0,[],target)并返回resres

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        if(not candidates):
            return []
        n=len(candidates)
        res=[]
        candidates.sort()
        def helper(i,tmp,target):
            if(target==0):
                res.append(tmp)
                return
            if(i==n or target<candidates[i]):
                return
            helper(i,tmp+[candidates[i]],target-candidates[i])
            helper(i+1,tmp,target)
        helper(0,[],target)
        return res