Python实现排队论——多坑位仿真（未使用仿真库，纯手写仿真）
Python实现排队论-多坑位厕所
在一次偶然机会，接触到运筹学的排队论问题，于是简单尝试了一下硬撸代码，纯手打仿真，没有使用仿真库。建议大家可以学习Simpy库，用以仿真。
一、案例:主要是基于“蒙特卡罗思想”，求解"单坑位"排队等待时间问题
场景：厕所排队问题
1、两场电影结束时间相隔较长，互不影响；
2、每场电影结束之后会有20个人想上厕所；
3、这20个人会在0到10分钟之内全部到达厕所；
4、每个人上厕所时间在1-3分钟之间
首先模拟最简单的情况，也就是厕所只有一个位置，不考虑两人共用的情况则每人必须等上一人出恭完毕方可进行。
分析：对于每个人都有如下几个参数：
到达时间 / 等待时间 / 开始上厕所时间 / 结束时间
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author:Dang
'''
Part1 设置随机值
'''
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
arrivingtime = np.random.uniform(0,10,size = 20)
arrivingtime.sort()
workingtime = np.random.uniform(1,3,size = 20)
# np.random.uniform 随机数：均匀分布的样本值
startingtime = [0 for i in range(20)]
finishtime = [0 for i in range(20)]
waitingtime = [0 for i in range(20)]
emptytime = [0 for i in range(20)]
# 开始时间都是0
print('arrivingtime\n',arrivingtime,'\n')
print('workingtime\n',workingtime,'\n')
print('startingtime\n',startingtime,'\n')
print('finishtime\n',finishtime,'\n')
print('waitingtime\n',waitingtime,'\n')
print('emptytime\n',emptytime,'\n')
'''
Part2 第一人上厕所时间
'''
startingtime[0] = arrivingtime[0]
# 第一个人之前没有人，所以开始时间 = 到达时间
finishtime[0] = startingtime[0] + workingtime[0]
# 第一个人完成时间 = 开始时间 + “工作”时间
waitingtime[0] = startingtime[0]-arrivingtime[0]
# 第一个人不用等待
print(startingtime[0])
print(finishtime[0])
print(waitingtime[0])
'''
Part3 第二人之后
'''
for i in range(1,len(arrivingtime)):
if finishtime[i-1] > arrivingtime[i]:
startingtime[i] = finishtime[i-1]
else:
startingtime[i] = arrivingtime[i]
emptytime[i] = arrivingtime[i] - finishtime[i-1]
# 判断：如果下一个人在上一个人完成之前到达，则 开始时间 = 上一个人完成时间，
# 否则 开始时间 = 到达时间，且存在空闲时间 = 到达时间 - 上一个人完成时间
finishtime[i] = startingtime[i] + workingtime[i]
waitingtime[i] = startingtime[i] - arrivingtime[i]
print('第%d个人：到达时间 开始时间 “工作”时间 完成时间 等待时间\n' %i,
arrivingtime[i],
startingtime[i],
workingtime[i],
finishtime[i],
waitingtime[i],
'\n')
print('arerage waiting time is %f' %np.mean(waitingtime))
"""
数据统计
"""
sns.set(style = 'ticks',context = "notebook")
fig = plt.figure(figsize = (8,6))
arrivingtime, = plt.plot(arrivingtime,label = 'arrivingtime')
startingtime, = plt.plot(startingtime,label = 'startingtime')
workingtime, = plt.plot(workingtime,label = 'workingtime')
finishtime, = plt.plot(finishtime,label = 'finishtime')
waitingtime, = plt.plot(waitingtime,label = 'waitingtime')
plt.title(("Queuing problem random simulation experiment").title())
plt.xlabel("Arriving Time(min)")
plt.ylabel("Total Time(min)")
plt.legend(handles=[arrivingtime,startingtime,workingtime,finishtime,waitingtime],
loc = 'upper left')
plt.show()
输出结果如下：
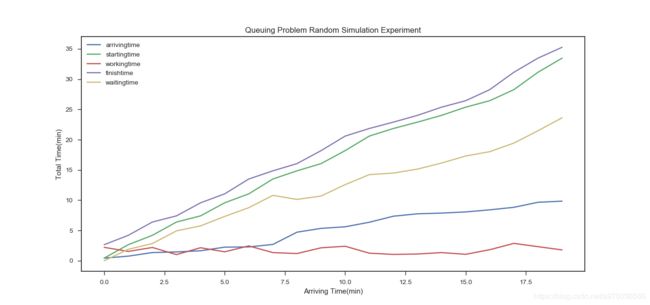以上为该网站内容：(https://www.cnblogs.com/yimengtianya1/p/8946338.html.
下文为我于上文基础上，继续推广到多坑位。
二、案例:主要是基于“蒙特卡罗思想”，求解"多坑位"排队等待时间问题
于一案例的基础假设上：
1.每个人不会插队
2.只有一条排队等待队列
3.不分男女厕所
4.假设从排队等待队列到坑位不需要花费时间
5.排队过程中不会有人放弃进入该厕所
6.排队讲究先来后到
7.每个人严格要求排队时间上厕所，忍耐时间无穷。
# -*- coding:utf-8 -*-
# Author:Xiangyang He
# Coding time: 10h
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns #用于合并绘图
#定义函数
class P(): #建立要上厕所的人对象
def __init__(self,Num,A,WK,WT,ET,FS,ST,R):
self.Num = Num #编号
self.A = A #到达时间 时间点
self.WT = WT #等待时间 时间长度
self.WK = WK #“工作”时间 时间长度
self.ET = ET #厕所无人空白时间 时间长度
self.FS = FS #完成工作时间 时间点
self.ST = ST #开始工作时间 时间点
self.R = R #剩余时间 时间长度
def toilet_which(toilet): #返回厕所队列中等待时间最短的索引
lt = []
for i in toilet:
lt.append(i.R)
return lt.index(min(lt))
def toilet_minus_test(toilet,m): #
h = []
for i in range(M):
if toilet[i] != None:
h.append(toilet[i].R-m)
if min(h)<=0:
return True
else:
return False
def toilet_None(toilet):
return [i for i,x in enumerate(toilet) if x == None ]
def toilet_0(toilet,m):
return [i for i,x in enumerate(toilet) if x != None and x.R <= m ]
def Nature_minus(x,y): #自然数集中的减法
if x>y:
return x-y
else:
return 0
#
N = 200 # item数量
M = 12 # 系统中处理item的个数
K = 30
np.random.seed(2333)
WK = np.random.uniform(10,5,size = N) #工作时间随机生成
A = np.random.uniform(0,K,size = N) #item到达时间随机生成
A.sort()
y = []
for i in range(0,N-1):
y.append(A[i+1]-A[i])
y = np.array(y)
Queue = [P(i,A[i],WK[i],0,0,0,0,0) for i in range(N)] #初始化Queue
#对toilet初始化
Queue[0].ST = Queue[0].A
Queue[0].WT = 0
Queue[0].ET = Queue[0].A
Queue[0].R = Queue[0].WK
toilet = [Queue[0]] + [None for i in range(M-1)]
lt = [] #等待的队伍
for k in range(1,N): #item陆续进入处理器与等待队伍
m = y[k-1]
if toilet_minus_test(toilet,m):
#print("toilet",toilet,end="")
s = list(set((toilet_None(toilet) + toilet_0(toilet,m))))
#print("这是关于A的Num",Queue[k].Num,"时刻为",Queue[k].A)
if len(lt) == 0:
print("1,1",Queue[k].Num)
v = s[0]
for i in range(M):
if i == v and toilet[v] == None:
Queue[k].ET = Queue[k].A
Queue[k].ST = Queue[k].A
toilet[v] = Queue[k]
if i == v and toilet[v] != None:
Queue[k].ET = m-toilet[v].R
Queue[k].ST = Queue[k].A
Queue[k].R = Queue[k].WK
toilet[v].FS = toilet[v].ST + toilet[v].WK
toilet[v].R = 0
toilet[v] = Queue[k]
if i != v:
if toilet[i]!=None:
toilet[i].R = Nature_minus(toilet[i].R,m)
if toilet[i].R == 0:
toilet[i].FS = toilet[i].ST + toilet[i].WK
toilet[i] = None
else:
lt.append(Queue[k])
#print("1,0apend",Queue[k].Num)
for i in range(M):
if i in s :
if len(lt) > 1:
toilet[i].FS = toilet[i].ST + toilet[i].WK
#print("前lt",lt[0].Num)
r = lt.pop(0)
#print("s",s)
#print("后lt",lt[0])
#print("第{}号厕所的{}完成".format(i,toilet[i].Num))
#print("取出",r.Num,"进入{}厕所".format(i))
r.ST = toilet[i].FS
r.ET = 0
r.R = r.WK - (m-toilet[i].R)
toilet[i].R = 0
toilet[i] = r
#if k == 10:
#print("ST",toilet[i].ST,toilet[i].Num,k)
if len(lt) == 1:
toilet[i].FS = toilet[i].ST + toilet[i].WK
toilet[i].R = 0
e = lt.pop(0)
e.ST = e.A
e.R = e.WK
toilet[i] = e
if len(lt) == 0:
toilet[i].FS = toilet[i].ST + toilet[i].WK
toilet[i].R = 0
toilet[i] = None
else:
toilet[i].R = Nature_minus(toilet[i].R,m)
else:
B = None in toilet
#if k ==2 :
#L = toilet[2]
#K = B
#print(toilet[2])
if B:
#print("0,1",Queue[k].Num)
v = toilet_None(toilet)
for i in range(M):
if i == v[0]:
Queue[k].ST = Queue[k].A
Queue[k].ET = 0
Queue[k].R = Queue[k].WK
toilet[i] = Queue[k]
#if k==2:
#print("asjdhaskjdhasd")
if i not in v:
toilet[i].R = Nature_minus(toilet[i].R,m)
else:
#print("0,0",Queue[k].Num)
for i in range(M):
toilet[i].R = Nature_minus(toilet[i].R,m)
lt.append(Queue[k])
#print("append",Queue[k].Num)
#for i in range(M):
# if toilet[i] != None:
#print("Num,",toilet[i].Num,"R",toilet[i].R)
#print("m",m)
while len(lt)!=0: #item已经到达，进入等待队伍
#print("lt的长度",len(lt))
v = toilet_which(toilet)
x = toilet[v].R
for i in range(M):
if i == v:
#print(toilet[v].Num,"在",v,"号厕所拉完",end="")
toilet[v].FS = toilet[v].ST + toilet[v].WK
toilet[v].R = 0
r = lt.pop(0)
#print(r.Num,"进入{}号厕所".format(v))
r.ST = toilet[v].FS
r.ET = 0
r.R = r.WK
toilet[v] = r
else:
toilet[i].R = Nature_minus(toilet[i].R,x)
for i in range(M): #处理器中剩下的工作
toilet[i].FS = toilet[i].ST + toilet[i].WK
toilet[i].R = 0
#print(toilet[i].Num,"在",i,"号厕所拉完",end="")
A = []
ST = []
WK = []
FS = []
WT= []
for i in range(N):
A.append(Queue[i].A)
ST.append(Queue[i].ST)
WK.append(Queue[i].WK)
FS.append(Queue[i].FS)
WT.append(Queue[i].WT)
A = np.array(A)
ST = np.array(ST)
WK = np.array(WK)
FS = np.array(FS)
WT = np.array(WT)
WT = ST - A
sns.set(style = "ticks", context = "notebook")
fig = plt.figure(figsize = (8,6))
arrivingtime, = plt.plot(A,label = "arrivingtime")
startingtime, = plt.plot(ST,label = 'startingtime')
workingtime, = plt.plot(WK,label = 'workingtime')
finishtime, = plt.plot(FS,label = 'finishtime')
waitingtime, = plt.plot(WT,label = 'waitingtime')
plt.title(("Queuing problem random simulation experiment about {} people to {} toilets".format(N,M)).title())
plt.xlabel("Arriving Time(min)")
plt.ylabel("Total Time(min)")
plt.legend(handles=[arrivingtime,startingtime,workingtime,finishtime,waitingtime],
loc = 'upper left')
plt.show()
print("{}个厕所{}分钟，对于{}人，平均每人等待{}分钟".format(M,K,N,np.mean(WT)))
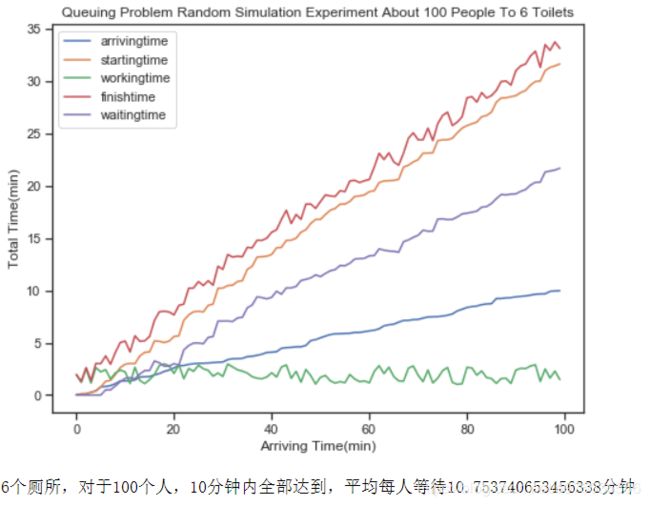
N = 100 # 需要上厕所的人数
M = 6 # 坑位
K = 10 #K分钟内所有人到达厕所
图像如下:
N = 100 # 需要上厕所的人数
M = 2 # 坑位
K = 10 #K分钟内所有人到达厕所
图像如下:
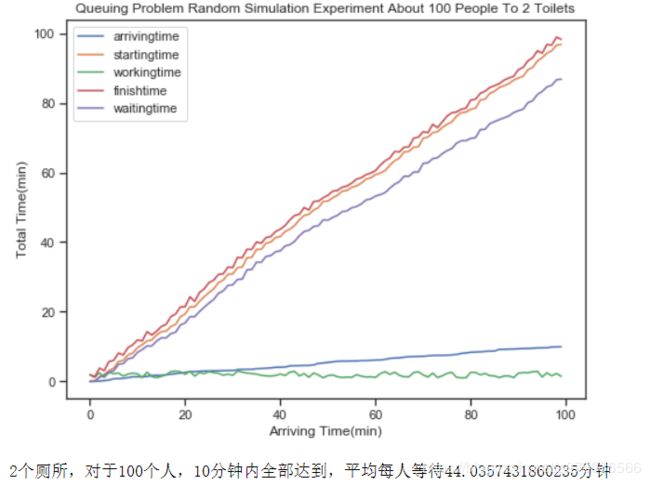可见，坑位增多可以显著减少平均等待时间。
以上是对于排队论的简单认识与实现，需要改进的地方有：
1.考虑残疾人与幼儿坑位，拟用增加一个单坑位代码，最后数据合并。
2.考虑特殊情况需要插队，拟用在对象中加入需要插队的反应器。
3.考虑男女厕所 ，拟用双等待队列。
4.考虑等待时间过长，有人放弃在此处上厕所，拟用在对象中加入放弃上厕所的反应器。
以上是我的拙见，coding过程中修改了四次，应该将算法考虑完善，再考虑完整coding。最后如果要使用大规模的仿真，建议大家学习Simpy库。