Octave常用操作(一)
笔记可能有点多,给自己提个醒,想到功能但想不起函数的时候直接用ctrl+F吧
目录
- 基础语法
- 在交互式中
- Octave中的变量
- Octave中的矩阵
- Octave中的help
- Octave中的移动数据
- Octave中的矩阵索引
- Octave中的数据计算
基础语法
% 注释
1/0 真/假
== 逻辑等于
~= 逻辑不等于
&& 逻辑与
|| 逻辑或
xor(1,0) 逻辑异或
在交互式中
PS1('>>'); 修改命令提示符
【注意】键入
a=3回车后下面会打印出a=3,如果不想让它打印就在语句后面加分号a=3;
Octave中的变量
>> a=pi; %pi表示圆周率,是个常量
>> a %输出打印a变量
a = 3.1416
>>
>> disp(a) %也可以这样输出
3.1416
>>
>> disp(sprintf('2 decimals: %0.2f', a)) %sprintf()生成一个字符串,格式的语法和C语言一样
2 decimals: 3.14
>>
>> format long %让字符串显示更长的位数
>> a
a = 3.14159265358979
>>
>> format short %让字符串显示较短的位数
>> a
a = 3.1416
>>
>> a^3 %a 的三次方
ans = 31.006
>>
Octave中的矩阵
>> A = [1 2; 3 4; 5 6] %空格分隔每行的元素,分号换行
A =
1 2
3 4
5 6
>>
>> v = 1:0.1:2 %定义一组数值v,从1到2,步长为0.1
v =
Columns 1 through 5:
1.0000 1.1000 1.2000 1.3000 1.4000
Columns 6 through 10:
1.5000 1.6000 1.7000 1.8000 1.9000
Column 11:
2.0000
>>
>> v = 1:6 %定义一组数值v,从1到6,步长默认为1
v =
1 2 3 4 5 6
>>
>> ones(2,3)
ans =
1 1 1
1 1 1
>>
>> C = 2*ones(2,3)
C =
2 2 2
2 2 2
>>
>> w = zeros(1,3)
w =
0 0 0
>>
>> eye(4) %生成一个4*4的单位矩阵
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>>
>> w = rand(1,3) %定义一个0到1的随机数的1*3矩阵
w =
0.89323 0.89065 0.59428
>>
>> w = randn(1,3) %得到3个随机数字,但它们服从正态分布,均值为0,标准差或者方差都为1
w =
0.27854 -0.12413 -1.07588
>>
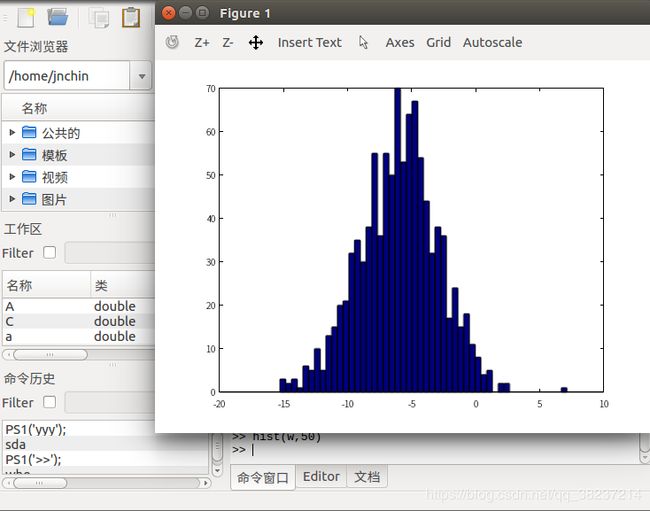
>> w = -6 + sqrt(10)*(randn(1,1000)); %设计一个更大的服从正态分布的一组数
>> hist(w,50) %将这组数用直方图画出来,50表示柱子的条数,可以不写,运行结果如下:
>>
>> A
A =
1 2
3 4
5 6
>>
>> size(A) %矩阵A(3行2列)的大小
ans =
3 2
>>
>> size(A,1) %矩阵A第一维度的大小,即行数
ans = 3
>>
>> v = [1 2 3 4 5]
v =
1 2 3 4 5
>> length(v) %表示矩阵最大维度的大小,为防止误解,我们经常只对向量使用length()函数,即向量中元素的个数
ans = 5
>>
Octave中的help
help eye或者help('eye')命令可以查看eye函数的具体用法,按q退出
Octave中的移动数据
pwd、cd、ls 这些命令和Linux命令功能基本一样,不必多说。
>> clear %清除内存中所有的变量,而命令 clear a 表示只清除变量a
>> who %显示Octave当前内存中的所有变量
>> load ex.dat %加载文件,等价于load('ex.dat')
>> whos %显示Octave当前内存中的所有变量,不过还显示变量的属性
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
ex 2x4 64 double
Total is 8 elements using 64 bytes
>> ex %此时文件ex.dat已经被加载到了变量ex中
ex =
1 2 3
4 5 6
7 8 9
10 11 12
>>
>> v = ex(2:10) %将ex的第二个到第十个元素赋值给v,不过是按列排序的。(与python的切片类似)
v =
4 7 10 2 5 8 11 3 6
>> size(v) %可以看出v是一个1行9列的行向量
ans =
1 9
>> b = ex(:) %将ex的所有元素赋值给b
b =
1
4
7
10
2
5
8
11
3
6
9
12
>> size(b) %可以看出b是一个12行1列的列向量
ans =
12 1
>>
>> save hello.mat v %把变量v的数据存入硬盘,保存为一个名为hell.mat的文件
>> save hello.txt b -ascii %把变量v的数据存入硬盘,保存为一个名为hell.txt的文件且编码为ascii
>> ls
ex.dat hello.mat hello.txt
当再次载入hello.mat文件时,你会发现内存中多了个变量v,它就是原先在保存hello.mat文件时的变量v
Octave中的矩阵索引
>> clear
>> A=[1 2;3 4;5 6]
A =
1 2
3 4
5 6
>> A(3,2) %矩阵索引,矩阵A的第3行第2列的数值
ans = 6
>> A(2,:) %矩阵A的第2行的所有数据
ans =
3 4
>>
>> A([1 3],:) %矩阵A的第一列和第三列数据
ans =
1 2
5 6
>>
>> A = [A,[100; 101; 102]] %在矩阵A的右边再加一列
A =
1 2 100
3 4 101
5 6 102
>>
>> C = [A B] %将A、B两个矩阵横着排在一起,等价于C = [A,B]
>> C = [A;B] %将A、B两个矩阵竖着排在一起
Octave中的数据计算
>> clear
>> A = [1 2;3 4;5 6]
A =
1 2
3 4
5 6
>> B = [1 2 3;4 5 6]
B =
1 2 3
4 5 6
>> C = [9 8;7 6;5 4]
C =
9 8
7 6
5 4
>>
>> A*B %矩阵A叉乘矩阵B
ans =
9 12 15
19 26 33
29 40 51
>> A.*C %矩阵A点乘矩阵B
ans =
9 16
21 24
25 24
>>
>> A.^2 %对A中每个元素求平方
ans =
1 4
9 16
25 36
>>
>> 1./A %对A中每个元素求倒数
ans =
1.00000 0.50000
0.33333 0.25000
0.20000 0.16667
>>
可以看出
.号代表对元素进行运算
>> log(A) %对A中每个元素求对数运算
ans =
0.00000 0.69315
1.09861 1.38629
1.60944 1.79176
>>
>> exp(A) %以e为底对A中每个元素为指数的幂运算
ans =
2.7183 7.3891
20.0855 54.5982
148.4132 403.4288
>>
>> abs(A) %对A中每个元素求绝对值
ans =
1 2
3 4
5 6
>>
>> -A %求每个元素的相反数,等价于 -1*v
ans =
-1 -2
-3 -4
-5 -6
>>
>> A+1 %每个元素都加1,等价于 A+ones(3,2) 或 A+ones([3 2]) 或 A+ones(size(A))
ans =
2 3
4 5
6 7
>>
>> A' %A的转置
ans =
1 3 5
2 4 6
>>
>> val = max(A) %求A中每一列中最大的元素
val =
5 6
>> max(A,[],1) %求A中每一列中最大的元素,同上
ans =
5 6
>> max(A,[],2) %求A中每一行中最大的元素
ans =
2
4
6
>> [val, ind]=max(A) %val是A中每一列中最大的元素,ind是对应的索引
val =
5 6
ind =
3 3
>> max(A,C) %取A和C中相互对应的较大元素
ans =
9 8
7 6
5 6
>>
>> A < 3 %A中各个元素与3做比较
ans =
1 1
0 0
0 0
>>
>> find(A < 3) %找到A中所有小于3的元素的索引
ans =
1
4
>>
>> D = magic(3) %生成一个幻方矩阵D,每行、每列、每条对角线的元素之和都相等
D =
8 1 6
3 5 7
4 9 2
>> [hang, lie] = find(D >= 7) %找到矩阵D中大于等于7的所有元素的行列索引
hang =
1
3
2
lie =
1
2
3
>>
>> a = [1 15 2 0.5] %定义一个向量a
a =
1.00000 15.00000 2.00000 0.50000
>> sum(a) %a中元素之和
ans = 18.500
>> prod(a) %a中元素之积
ans = 15
>>
>> floor(a) %向下取整
ans =
1 15 2 0
>> ceil(a) %向上取整
ans =
1 15 2 1
>>
>> A
A =
1 2
3 4
5 6
>> flipud(A) %上下翻转
ans =
5 6
3 4
1 2
>>
>> pinv(A) %求A矩阵的逆矩阵,即使A不可逆,所以这里是伪逆
ans =
-1.33333 -0.33333 0.66667
1.08333 0.33333 -0.41667
>>
参考课程:《吴恩达机器学习》