python-霍夫曼编码实现压缩和解压缩（一）

1.霍夫曼编码

霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，通过采用不等长的编码方式，将出现频率高的符号用相对短的比特串表示、出现频率低的符合以相对长的比特串表示，能够缩短表示完整源数据所需要的总比特长度，从而达到无损压缩数据的效果。

2.霍夫曼树

以下内容来源：

版权声明：本文为CSDN博主「字节莫」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43690347/article/details/84146979

哈夫曼编码基于哈夫曼树(Huffman Tree)来实现，哈夫曼树是将符号出现的频率作为叶子的权值所构建一棵二叉树。我们以一个例子来详细解释哈夫曼树。

有这么一句话：“This is a test str”

字符	T	h	i	s	a	e	t	r
频率	1	1	2	4	1	1	3	1

上表就是这句话中各个字符出现的频率统计（由于空格的表示效果不好，因此此示例中空格忽略不计）。

权值的顺序如下：

1（T）、1（h）、1（a）、1（e）、1（r）、2（i）、3（t）、4（s）

2.1 对权值排序，取最小的两个生成节点

取T、h，生成一个小二叉树：

2.2 重新对所有根节点的权值进行排序并生成父节点

没有父节点的节点为根节点。例如上一步骤中的“T”“h”节点有父节点，那么它们就不是根节点，不参与排序。重新对所有根节点进行排序如下：

1（a）、1（e）、1（r）、2（T、h）、2（i）、3（t）、4（s）

生成的二叉树如下：

两个子节点生成的父节点的权值为两个子节点之和

2.3 重复进行排序、生成父节点，直到只剩下一个根节点

反复进行排序和生成父节点直到只剩下一个根节点，我们可以构建出这样一棵二叉树：

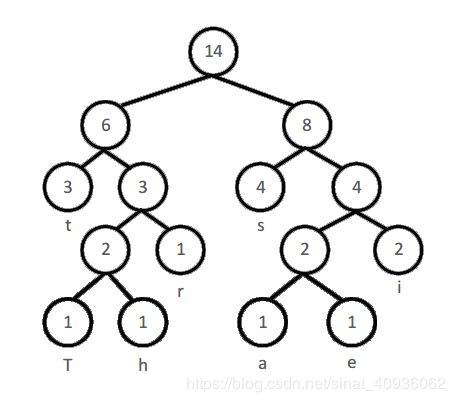
我们定义每个结点的左子节点编号为0，右子节点编号为1，那么可以得到如下的编码表：

字符	编码
T	0010
h	1010
i	111
s	01
a	0011
e	1011
t	00
r	110

那压缩的效果如何？我们来对比一下压缩前后表示这个字符串所需要的比特串长度：

压缩前（ASCII编码）：

一个字符编码长度（8比特位）× 字符数量（14）= 112比特

压缩后：

T（4）+ h（4）+ a（4）+ e（4）+ r（3）+ i（3×2）+ t（2×3）+ s（2×4）= 39比特

压缩的效果显而易见。
（基于哈夫曼编码的压缩算法并非对所有源数据都能起到同样的压缩效果，这一点我们会在后面讲到）

3.基于哈夫曼编码的压缩算法的Python实现

基于以上的哈夫曼编码算法，我们可以实现自己的压缩算法。

3.1 定义哈夫曼树的节点类

为了使思路更加清晰、有助于算法实现，我们可以将单个节点定义为一个类，从而大大简化了二叉树的维护机制。

class node(object):
 
    def __init__(self,value = None,left = None,right = None,father = None):
        self.value = value
        self.left = left
        self.right = right
        self.father = father
 
    def build_father(left,right):
    	n = node(value = left.value + right.value,left = left,right = right)
    	left.father = right.father = n
    	return n
 
    def encode(n):
    	if n.father == None:
    		return b''
    	if n.father.left == n:
    		return node.encode(n.father) + b'0'		#左节点编号'0'
    	else:
    		return node.encode(n.father) + b'1'		#右节点编号'1'

3.2 构建哈夫曼树

由于哈夫曼编码的过程中有许多步骤重复执行，因此在节点类的基础上，借助递归的思想来完成哈夫曼树的构建。
一个具有注脚的文本。[^2]

def build_tree(l):
 
	if len(l) == 1:
		return l
	sorts = sorted(l,key = lambda x:x.value,reverse = False)
	n = node.build_father(sorts[0],sorts[1])
	sorts.pop(0)
	sorts.pop(0)
	sorts.append(n)
	return build_tree(sorts)

3.3 利用构建好的哈夫曼树进行编码

在上一步中构建好的哈夫曼树的基础上进行编码：

def encode(echo):
 
	for x in node_dict.keys():
		ec_dict[x] = node.encode(node_dict[x])
		if echo == True:						#输出编码表（用于调试）
			print(x)
			print(ec_dict[x])

3.4 实现文件压缩、解压函数

既然我们实现的是压缩算法，那么就必须能够实现文件的压缩、解压操作才有意义。如果只能实现字符串的编码或者压缩解压，是没有很大的实用价值的。

文件压缩：

def encodefile(file):
 
	print("Starting encode...")
	f = open(file,"rb")
	bytes_width = 1						#每次读取的字节宽度
	i = 0
 
	f.seek(0,2)
	count = f.tell() / bytes_width
	print(count)
	nodes = []							#结点列表，用于构建哈夫曼树
	buff = [b''] * int(count)
	f.seek(0)
 
	#计算字符频率,并将单个字符构建成单一节点
	while i < count:
		buff[i] = f.read(bytes_width)
		if count_dict.get(buff[i], -1) == -1:
			count_dict[buff[i]] = 0
		count_dict[buff[i]] = count_dict[buff[i]] + 1
		i = i + 1
	print("Read OK")
	print(count_dict)
	for x in count_dict.keys():
		node_dict[x] = node(count_dict[x])
		nodes.append(node_dict[x])
	
	f.close()
	tree = build_tree(nodes)		#哈夫曼树构建
	encode(False)					#构建编码表
	print("Encode OK")
 
	head = sorted(count_dict.items(),key = lambda x:x[1] ,reverse = True)
	bit_width = 1
	print("head:",head[0][1])					#动态调整编码表的字节长度，优化文件头大小
	if head[0][1] > 255:
		bit_width = 2
		if head[0][1] > 65535:
			bit_width = 3
			if head[0][1] > 16777215:
				bit_width = 4
	print("bit_width:",bit_width)
	i = 0
	raw = 0b1
	last = 0
	name = file.split('.')
	o = open(name[0]+".ys" , 'wb')
	o.write(int.to_bytes(len(ec_dict) ,2 ,byteorder = 'big'))		#写出结点数量
	o.write(int.to_bytes(bit_width ,1 ,byteorder = 'big'))			#写出编码表字节宽度
	for x in ec_dict.keys():										#编码文件头
		o.write(x)
		o.write(int.to_bytes(count_dict[x] ,bit_width ,byteorder = 'big'))
 
	print('head OK')
	while i < count:												#开始压缩数据
		for x in ec_dict[buff[i]]:
			raw = raw << 1
			if x == 49:
				raw = raw | 1
			if raw.bit_length() == 9:
				raw = raw & (~(1 << 8))
				o.write(int.to_bytes(raw ,1 , byteorder = 'big'))
				o.flush()
				raw = 0b1
				tem = int(i  /len(buff) * 100)
				if tem > last:
					print("encode:", tem ,'%')						#输出压缩进度
					last = tem
		i = i + 1
 
	if raw.bit_length() > 1:										#处理文件尾部不足一个字节的数据
		raw = raw << (8 - (raw.bit_length() - 1))
		raw = raw & (~(1 << raw.bit_length() - 1))
		o.write(int.to_bytes(raw ,1 , byteorder = 'big'))
	o.close()
	print("File encode successful.")

解压文件：

def decodefile(inputfile, outputfile):
 
	print("Starting decode...")
	count = 0
	raw = 0
	last = 0
	f = open(inputfile ,'rb')
	o = open(outputfile ,'wb')
	f.seek(0,2)
	eof = f.tell()
	f.seek(0)
	count = int.from_bytes(f.read(2), byteorder = 'big')			#取出结点数量
	bit_width = int.from_bytes(f.read(1), byteorder = 'big')		#取出编码表字宽
	i = 0
	de_dict = {}
	while i < count:												#解析文件头
		key = f.read(1)
		value = int.from_bytes(f.read(bit_width), byteorder = 'big')
		de_dict[key] = value
		i = i + 1
	for x in de_dict.keys():
		node_dict[x] = node(de_dict[x])
		nodes.append(node_dict[x])
	tree = build_tree(nodes)					#重建哈夫曼树
	encode(False)								#建立编码表
	for x in ec_dict.keys():					#反向字典构建
		inverse_dict[ec_dict[x]] = x
	i = f.tell()
	data = b''
	while i < eof:								#开始解压数据
		raw = int.from_bytes(f.read(1), byteorder = 'big')
		# print("raw:",raw)
		i = i + 1
		j = 8
		while j > 0:
			if (raw >> (j - 1)) & 1 == 1:
				data = data + b'1'
				raw = raw & (~(1 << (j - 1)))
			else:
				data = data + b'0'
				raw = raw & (~(1 << (j - 1)))
			if inverse_dict.get(data, 0) != 0:
				o.write(inverse_dict[data])
				o.flush()
				#print("decode",data,":",inverse_dict[data])
				data = b''
			j = j - 1
		tem = int(i / eof * 100)
		if tem > last:							
			print("decode:", tem,'%')			#输出解压进度
			last = tem
		raw = 0
 
	f.close()
	o.close()
	print("File decode successful.")

4.总结

综上，基于纯哈夫曼算法的压缩程序能够对未经压缩的文件格式起到压缩作用，特别是对字节种类不多、重复次数多的文件格式如bmp位图、avi视频等能够起到非常好的压缩效果，但对于本身已经经过压缩的文件格式如docx、mp4等基本无效。

完整代码文件请见文中引用博客的github账户，但是存在问题，解决后就可以实现文件的无损压缩了。具体问题分析，以及代码的详细注释，请看下一篇《python-霍夫曼编码实现压缩和解压缩（二）》