残差、方差、偏差、MSE均方误差、Bagging、Boosting、过拟合欠拟合和交叉验证

数据和模型 https://blog.csdn.net/u010986753/article/details/98526886

一、残差、方差、偏差

1.1 残差统计概念

  残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话， 我们可以将残差看作误差的观测值。

  在回归分析中，测定值与按回归方程预测的值之差，以δ表示。残差δ遵从正态分布N(0，σ2)。（δ-残差的均值）/残差的标准差，称为标准化残差，以δ表示。δ遵从标准正态分布N(0，1)。实验点的标准化残差落在(-2，2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2，2)区间以外，可在95%置信度将其判为异常实验点，不参与回归直线拟合。

  显然，有多少对数据，就有多少个残差。残差分析就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰。残差计算即是残差的平方和除以(残差个数-1)的平方根。

1.2 方差、标准差

  Variance反映的是模型每一次输出结果与模型输出期望（即均值） 之间的误差，即模型的稳定性。

  概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。

  描述模型对于给定值的输出稳定性。 度量同样大小的训练集的变动所导致的学习性能的变化，刻画数据扰动所产生的影响

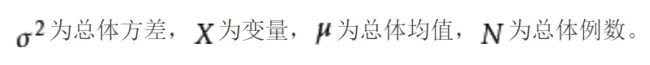
  1）方差：方差是在概率论和统计方差衡量随机变量或一组数据的离散程度的度量方式，方差越大，离散度越大。求解方式为，各随机变量与平均值差值的平方和的平均数（先求差，再平方，再平均）

  2）标准差：标准差就是方差的算术平方根，它反映组内个体间的离散程度。因此它的过程是与平均值之间进行差值计算。

• 1、均方差就是标准差，标准差就是均方差
• 2、均方误差不同于均方误差
• 3、均方误差是各数据偏离真实值的距离平方和的平均数

1.3 偏差

  首先error=bias+variance，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精确度。

  偏差又称为表观误差，是指个别测定值与测定的平均值之差，它可以用来衡量测定结果的精密度高低。在统计学中常用来判定测量值是否为坏值。精密度是指一样品多次平行测定结果之间的符合程度，用偏差表示。偏差越小，说明测定结果精密度越高。

  描述模型输出结果的期望与样本真实结果的偏离程度。

• δ是均方根误差亦称标准误差

1.4 残差、方差、偏差总结

• 简单模型：偏差大，方差小（简单模型受样本值的影响较小，稳定性高），容易造成欠拟合
• 复杂模型：偏差小，方差大，容易产生过拟合
• 判断偏差大还是方差大：
  1）模型上的训练样本的真实值较少，则偏差大（欠拟合）
  2）在训练样本上样本拟合的较好，但在测试集上拟合较差，则方差大（过拟合Overfiting）
  3）当偏差较大时，表示目标可能未在模型上（即未瞄准靶心），需要重新训练model（有可能未考虑其他因素对样本的影响，或者应让模型更复杂考虑更高次幂的情况）。增加网络层数，增加隐藏层神经元数量，增加算法迭代次数，或者用更好的优化算法。
  4）当方差较大时：增加更多的数据或正则化

1.5 MSE、RMSE、MAE

  RMSE

• Root Mean Square Error,均方根误差

• 是观测值与真值偏差的平方和与观测次数m比值的平方根。

• 是用来衡量观测值同真值之间的偏差
  MAE

• Mean Absolute Error ，平均绝对误差

• 是绝对误差的平均值

• 能更好地反映预测值误差的实际情况.
  标准差

• Standard Deviation ，标准差

• 是方差的算数平方根

• 是用来衡量一组数自身的离散程度

  总的来说，均方差是数据序列与均值的关系，而均方误差是数据序列与真实值之间的关系，所以我们只需要搞清楚真实值和均值之间的关系就行了。

• RMSE与标准差对比：标准差是用来衡量一组数自身的离散程度，而均方根误差是用来衡量观测值同真值之间的偏差，它们的研究对象和研究目的不同，但是计算过程类似。

• RMSE与MAE对比：RMSE相当于L2范数，MAE相当于L1范数。次数越高，计算结果就越与较大的值有关，而忽略较小的值，所以这就是为什么RMSE针对异常值更敏感的原因（即有一个预测值与真实值相差很大，那么RMSE就会很大）。

  MSE均方误差 mean-square error作为机器学习中常常用于损失函数的方法，均方误差频繁的出现在机器学习的各种算法中，但是由于是舶来品，又和其他的几个概念特别像，所以常常在跟他人描述的时候说成其他方法的名字。通过计算每个预测值和实际值之间的差值的平方和再求平均，机器学习中它经常被用于表示预测值和实际值相差的程度。
  均方误差的数学表达为：

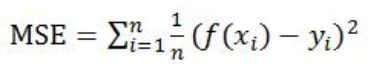
y_preditc=reg.predict(x_test) #reg是训练好的模型 
mse_test=np.sum((y_preditc-y_test)**2)/len(y_test) #跟数学公式一样的作者：skullfang

  4）RMSE：公式

#RMSE实现
rmse_test=mse_test ** 0.5

1.6 代码实现

• MAE

mae_test=np.sum(np.absolute(y_preditc-y_test))/len(y_test)

• R-square(确定系数)
    R Squared也就R方，其中分子是Residual Sum of Squares 分母是 Total Sum of Squares
  那就看公式吧

1- mean_squared_error(y_test,y_preditc)/ np.var(y_test)

• scikit-learn中的各种衡量指标

from sklearn.metrics import mean_squared_error #均方误差
from sklearn.metrics import mean_absolute_error #平方绝对误差
from sklearn.metrics import r2_score#R square
#调用
mean_squared_error(y_test,y_predict)
mean_absolute_error(y_test,y_predict)
r2_score(y_test,y_predict)

二、Bagging和Boosting的区别

决策树Decision Tree 和随机森林RandomForest基本概念（一）https://blog.csdn.net/u010986753/article/details/100144214

2.1 基本介绍

  Baggging 和Boosting都是模型融合的方法，可以将弱分类器融合之后形成一个强分类器，而且融合之后的效果会比最好的弱分类器更好。

2.2 Bagging:

  Bagging即套袋法，其算法过程如下：

  从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）

  每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）

  对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

2.3 Boosting：

  AdaBoosting方式每次使用的是全部的样本，每轮训练改变样本的权重。下一轮训练的目标是找到一个函数f 来拟合上一轮的残差。当残差足够小或者达到设置的最大迭代次数则停止。Boosting会减小在上一轮训练正确的样本的权重，增大错误样本的权重。（对的残差小，错的残差大）

  梯度提升的Boosting方式是使用代价函数对上一轮训练出的模型函数f的偏导来拟合残差。AdaBoosting方式每次使用的是全部的样本，每轮训练改变样本的权重。下一轮训练的目标是找到一个函数f 来拟合上一轮的残差。当残差足够小或者达到设置的最大迭代次数则停止。Boosting会减小在上一轮训练正确的样本的权重，增大错误样本的权重。（对的残差小，错的残差大）

  梯度提升的Boosting方式是使用代价函数对上一轮训练出的模型函数f的偏导来拟合残差。

2.4 Bagging，Boosting二者之间的区别

1）样本选择上：

  Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。

  Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

2）样例权重：

  Bagging：使用均匀取样，每个样例的权重相等

  Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

3）预测函数：

  Bagging：所有预测函数的权重相等。

  Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

4）并行计算：

  Bagging：各个预测函数可以并行生成

  Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

5）bagging减少variance，而boosting是减少bias
  Bagging对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。由于子样本集的相似性以及使用的是同种模型，因此各模型有近似相等的bias和variance（事实上，各模型的分布也近似相同，但不独立）。另一方面，若各子模型独立，则有，此时可以显著降低variance。若各子模型完全相同，则此时不会降低variance。bagging方法得到的各子模型是有一定相关性的，属于上面两个极端状况的中间态，因此可以一定程度降低variance。

  boosting是在sequential地最小化损失函数，其bias自然逐步下降。但由于是采取这种sequential、adaptive的策略，各子模型之间是强相关的，于是子模型之和并不能显著降低variance。所以说boosting主要还是靠降低bias来提升预测精度。

三、过拟合欠拟合

3.1 Underfit (欠拟合) high bias

  模型拟合不够，在训练集（training set）上表现效果差，没有充分的利用数据，预测的准确度低。

3.1 Overfit（过拟合）high viarance

  模型过度拟合，在训练集（training set）上表现好，但是在测试集上效果差，也就是说在已知的数据集合中非常好，但是在添加一些新的数据进来训练效果就会差很多，造成这样的原因是考虑影响因素太多，超出自变量的维度过于多了。

3.1 过拟合欠拟合总结

  如何防止过拟合（过拟合主要使有两个原因造成的：数据太少+模型太复杂。）：

  ❶ 获取更多数据，这是解决过拟合最有效的方法，只要给足够多的数据，让模型[训练到]尽可能多的[例外情况]，它就会不断修正自己，从而得到更好的结果。
  ❷ 减少特征变量，减少网络的层数、神经元的个数等均可以限制网络的拟合能力；
  ❸ 限制权值（正则化）
  ❹ 贝叶斯方法
  ❺ 结合多种模型

四、交叉验证介绍

数据集划分train_test_split\交叉验证Cross-validationhttps://blog.csdn.net/u010986753/article/details/98069124

  交叉验证用在数据不是很充足的时候。比如在我日常项目里面，对于普通适中问题，如果数据样本量小于一万条，我们就会采用交叉验证来训练优化选择模型。如果样本大于一万条的话，我们一般随机的把数据分成三份，一份为训练集（Training Set），一份为验证集（Validation Set），最后一份为测试集（Test Set）。

• 训练集来训练模型
• 验证集来评估模型预测的好坏和选择模型及其对应的参数
• 测试集，把最终得到的模型再用于测试集，最终决定使用哪个模型以及对应参数。

'''
【干货来了|小麦苗IT资料分享】
★小麦苗DB职场干货：https://mp.weixin.qq.com/s/Vm5PqNcDcITkOr9cQg6T7w
★小麦苗数据库健康检查：https://share.weiyun.com/5lb2U2M
★小麦苗微店：https://weidian.com/s/793741433?wfr=c&ifr=shopdetail
★各种操作系统下的数据库安装文件（Linux、Windows、AIX等）：链接：https://pan.baidu.com/s/19yJdUQhGz2hTgozb9ATdAw  提取码：4xpv
★小麦苗分享的资料：https://share.weiyun.com/57HUxNi
★小麦苗课堂资料：https://share.weiyun.com/5fAdN5m
★小麦苗课堂试听资料：https://share.weiyun.com/5HnQEuL
★小麦苗出版的相关书籍：https://share.weiyun.com/5sQBQpY
★小麦苗博客文章：https://share.weiyun.com/5ufi4Dx
★数据库系列（Oracle、MySQL、NoSQL）：https://share.weiyun.com/5n1u8gv
★公开课录像文件：https://share.weiyun.com/5yd7ukG
★其它常用软件分享：https://share.weiyun.com/53BlaHX
★其它IT资料（OS、网络、存储等）：https://share.weiyun.com/5Mn6ESi
★Python资料：https://share.weiyun.com/5iuQ2Fn
★已安装配置好的虚拟机：https://share.weiyun.com/5E8pxvT
★小麦苗腾讯课堂：https://lhr.ke.qq.com/
★小麦苗博客：http://blog.itpub.net/26736162/
'''

'''
如需转发，请注明出处：小婷儿的博客python    https://blog.csdn.net/u010986753

  CSDN https://blog.csdn.net/u010986753

  博客园 https://www.cnblogs.com/xxtalhr/

有问题请在博客下留言或加作者：
  微信：tinghai87605025 联系我加微信群
  QQ ：87605025
  QQ交流群：py_data 483766429
  公众号：DB宝

证书说明
  OCP证书说明连接 https://mp.weixin.qq.com/s/2cymJ4xiBPtTaHu16HkiuA

  OCM证书说明连接 https://mp.weixin.qq.com/s/7-R6Cz8RcJKduVv6YlAxJA
'''

有趣的事，Python永远不会缺席

欢迎关注小婷儿的博客

  文章内容来源于小婷儿的学习笔记，部分整理自网络，若有侵权或不当之处还请谅解!!!

   小婷儿的python正在成长中，其中还有很多不足之处，随着学习和工作的深入，会对以往的博客内容逐步改进和完善哒。重要的事多说几遍。。。。。。