电路课组（一）电路原理 Part 1电路分析概述：分析思想与描述电路的基本量

1. 电路分析的背景和基本思想

1.1. 电路研究对象

实际电路系统是由电路元件组成的电流通路装置。

电路系统遵从一般电学规律，即符合Maxwell方程的约束。
但是我们很容易发现，微分方程的复杂性，使得电学问题的求解非常困难。
这也正是电路分析的精妙和简洁之处。

所以我们在符合工程误差的情况下，对Maxwell方程中的部分进行理论抽象，形成一类理想模型，这些理想元件分别可以对应Maxwell方程中的一项，或由某个特定的方程表出。
我们的电路分析，就是对这类的电路抽象模型的研究。

1.2. 电路抽象与电路抽象的三原则

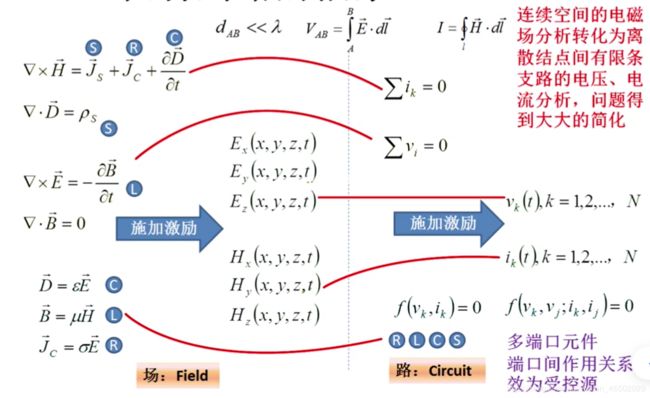
1.2.1. Maxwell方程中的对应抽象

前面已经说到，电路的理论本质仍是Maxwell方程。
比如在这张图中我们可以看出：

• Ampere全电流定律中各项可以对应表示为电源产生电流、电阻抵抗电流，电场(D可以表征电场强度)的变化产生电流，也就是电容效应；
• Gauss定律对应的含义是电源电动势可以带动产生电流；
• 法拉第电磁感应定律对应的含义是电流变化引发电压变化，这也就是电感的实质。

这里特别要注意，在建立这种抽象的时候，Maxwell方程中B、H、I在描述磁场，E、D、U在描述电场，在思考这种对应的时候，脑子要灵光一点~

1.2.2. 抽象原则

离散化原则

所谓离散就是可数。核心本质是等效。

这和算法当中的离散化是一致的，我们不需要考察本有的数据特征，只需要让它们获得可数的性质，问题得到解决的同时，解决过程大大简化。换句话说，我们损失了一部分信息，但是那一部分信息对解决问题是没有意义的。

我们不需要考虑元件当中的构造特征以及其中连续的场的性质，只需要考察端口处的行为。从而使得对场的微分方程，转化成离散的元件之间的参量代数问题。
这就是所谓的离散化原则。

离散化的应用除了将场视作路以外，还有可数分区的想法。比如MOSFET的特性呈现线性区、饱和区和击穿区，而不是整体使用一条复杂的曲线进行拟合。

另外广义KCL和KVL也是一种离散化思想的体现。

极致化原则

所谓极致就是走极端，追求简单的完美，忽略繁杂的细枝末节。代表着有意义的工程近似。
在数学上的简单描述就是：
$$|a|\gg |b|\Rightarrow \{\begin{array}{l}a+b=a\\ \frac{1}{a}+\frac{1}{b}=\frac{1}{b}\end{array}$$
在科学史中，往往是先出现了实际元件才抽象成新的电路模型。
如果我们抽象出的模型的电气关系通实际元件性能相当接近，则称建立了该实际元件的电路模型。这就是一种极致化的思路。

实际系统由大量元件组成，如果所有都进行写实的刻画、精确的描述，会使得分析过程相当繁杂，不能适应工程实际的需要。
因此我们通过极致化的想法，对电路模型的精度和求解的难度上综合考虑。这也叫工程近似。这样可以使我们在简洁的情形下得到简单的原理性结论，从而快速有效地进行原理性设计。

没有极致化的想法，就会淹没在复杂混乱的思路和混乱的公式推导之中。

极致化主要的应用有：

• 忽略分布特性，仅考虑集总电路特性。
• 导线、理想电流表、独立电压源视为短接，理想电压表、独立电流源视为断路。
• 运放中的虚短虚断。

限定性原则

在前述的简化当中，我们都有一些限定性的条件；这种主次要的限定关系，虽然使得问题得到简化，但也要求我们注意其使用条件，超过适用范围，就不能进行原理性的抽象。

比如频率增大时，导线中的趋肤效应越发显著，不能再使用集总电路的分析方法。
继续增大时，感生磁场的电感效应，以及导线之间的寄生电容，都会使得问题进一步复杂化，最终脱离典型电路的分析范围之后就只能使用电动力学方法求解了。所以说第三点是在使用简化的时候，时刻要牢记的。

1.3. 电路分析模型的建立

经过以上的分析，我们已经对电路分析的观点有了相对深刻的理解。现在我们总结一下主要的电路模型：

电源

电路的基本功能有两大类，为能量处理和信号处理。但不管是电能还是电信号，都需要一个来源。这个来源处电压和电流为非关联参考方向，能量放出，因而这种方向也称为有源符号规定。
其他部件称为负载。在在电路中电源的效应称为激励，负载称为响应。负载中的电压电流方向为关联参考方向，即由电压被动产生电流的方向。

这个参考方向不与因其是电源或是负载直接决定，重要的是判断方向。

电阻、电感和电容

如果不关心元件内部结构和能量转化的物理过程，那么很简单地可以表示成：

• 电阻消耗能量。
• 电感存储磁场能
• 电容存储电场能。

端口

如果不关心元件内部的电磁场性质，可以将其封装起来，使其与外界仅有交互的通道进行交流。这是我们进行进行元件抽象时的离散化思路。
如果对一个子网络都不感兴趣，只关心其外部特性，可以继续增大离散的程度（将子网络封装起来，进一步减少元件数量，减少电路系统中的信息量），简化计算。MOSFET就是这样的典型例子。

一个子电路上一个接线端称为一个端钮，或端，如果两个端一进一出、电流相等，那么这两个端就组成这个子电路的一个端口。

tips：

• 电流大小相等称为两个端的端口条件。这也体现了抽象原则当中的限定性原则。
• 结合先前在电源部分中提到的参考方向，端口可以分为有源、和无源两种端口。

二端口网络是重要的。一方面它可以用来对很多电路网络进行建模，另一方面它是最简单的多端口网络。
二端口网络有时可以简称为二端口。

1.4. 电路分析的基本思想

基本思想蕴含在以上的阐述中，总结如下：

1. 抽象的思想。我们通过抽象描述主要的分析问题，并通过合理的建模对待求值进行相对精确的预测。
2. 工程近似。与抽象紧密相关，抽象建模的精度和电路求解的方便程度不能兼得，所以要进行符合精度的近似，这和抽象的极致化原则是一致的。
3. 等效思想。通过等效，可以简化繁杂的运算，这和数学中寻找代数系统的想法是一致的。

   关于等效，在电路中等效网络的结论可以迁移，比如独立电流源具有和断路类似的性质，在列KVL的时候，要尽量避免使用其所在的支路。

2. 电路的基本描述方法

由前述，电路理论是由电磁场理论抽象而来。电磁场理论有4个基本量：$$\mathbf{E},\mathbf{D},\mathbf{B},\mathbf{H}$$
对应在电路中，有4个相对应的基本量
$$u,q,\Psi ,i$$
其中$u,i$容易测量，多用之分别表征电场和磁场特性。
这里讨论电流、电压以及其相乘可得的功率。

2.1. 电流

它通过Ampere全电流定律表征磁场性质。

与中学不同的是，这里电流要考虑方向。类似力学中的假设法思路。
表示电流方向的三种方法：

1. 箭头标注
2. 双下标法
3. 正负号

电位降和电流方向相同称为关联参考方向。这在1.3电源中已经讨论过。
恒定电流用大写$I$表示，变化电流用$i$表示，也可写作$i(t)$

2.2. 电压和电动势

电压是两点之间的关系。
为了表征一点电压的特性，可以选定一个参考点。使得：
$${\phi }_A=u_{AP}$$
同于电流，大写表示恒定，小写表变化。

电动势是描述电源内部性质的物理量，表示电源负极到正极的电位升。在数值上可以用电压表示。永远是正值
$$e_{BA}=u_{AB}$$
而电压是电路元件上的电位降，因方向不同可正可负。

2.3. 能量描述：功率

对一个电路元件，选定其电压和电流方向使之为关联参考方向：
$$P_a=ui\{\begin{array}{ll}>0,& 吸收能量\\ <0,& 放出能量\end{array}$$
吸收的能量在三种基本元件上分别转化为热能、磁场能和电场能。
另外可以在非关联参考方向上，计算放出功率，其在数值上有：
$$P_d=-P_a\{\begin{array}{ll}>0,& 放出能量\\ <0,& 吸收能量\end{array}$$