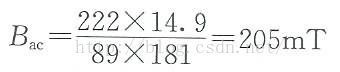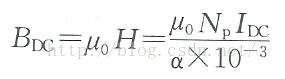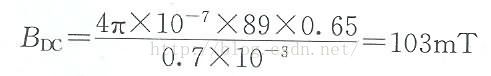磁通 磁通量 磁链 磁通密度 磁场强度 交流磁通密度 直流磁通密度 最大磁通密度 ... .. ...
若磁场通过能导电的电线环,而磁通量的改变的话,会引起电动势的生成, 并因此会产生电流(在环中)。其关系式可由法拉第定律得出:
| 磁芯的直流偏置与交流磁通密度 | |
在直流偏置电流作用下,由于饱和作用,MPP磁芯的磁导率呈现减小趋势。图1显示了这种趋势,对高磁导率这种变化更加明显。为了利用该曲线进行设计,设计中的磁动势(磁化力)用式(9.2)进行计算。若磁导率的减小使电感量的下降不超过30%,则可以用增加线圈匝数的方法补偿偏置造成的影响。若磁导率的降低超过了30%,增加匝数会造成磁导率的进一步下降,且比N2快。因此要用更大的磁芯才能解决问题。
|
|
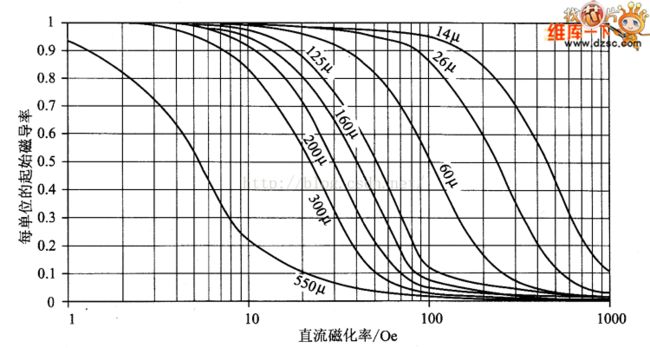
图1 磁导率和直流偏置的关系
磁芯磁导率也随交流磁通密度改变,如图2(a)所示。由式(9.6)可以计算磁通密度。 随着交流磁通密度增加,磁导率在初始阶段升高,然后大约在20006后下降。采用较大的磁芯可减少磁通密度。频率对较高磁导率也有影响,如图2(b)所示。当磁通密度在2006以下时,磁芯损耗是一个常数。然而,当激励增加时,对Q值的影响可能有相反作用。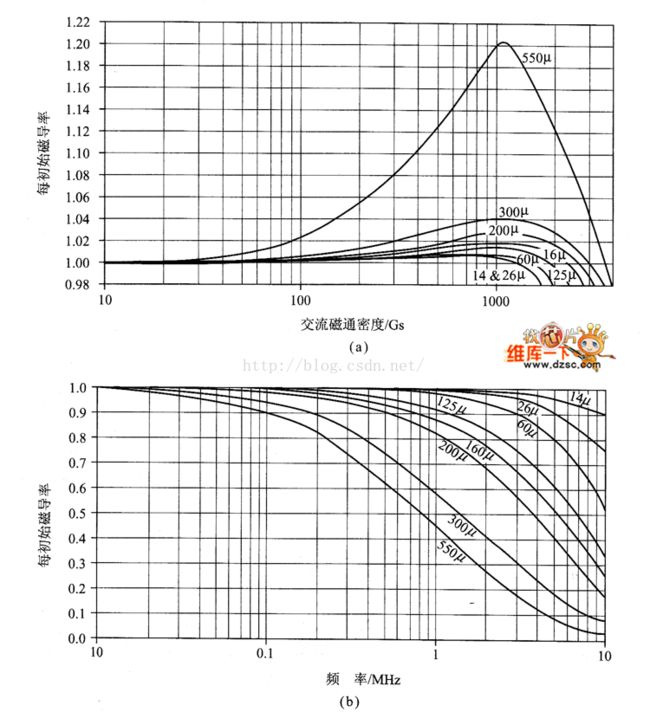
图2 磁导率与交流磁通密度、频率的关系
磁感应强度在数值上可以看成为与磁场方向垂直的单 位面积所通过的 磁通,故又称为 磁通密度。
磁通密度与磁感强度区别在于后者为矢量有方向,前者无方向
在保证在磁心的最大工作值和饱和值之间有足够的裕量,需要检验磁心的最大磁通密度。在任何条件下,包括瞬间负载和高温,防止磁心饱和是很重要的。这可以用两种方法来检验:在变换器中进行测量或计算。
注意:建议无论使用何种设计方法,都应进行该检验,以保证最后一切如愿以偿。
(1)在控制仍能维持的情况下,使输入电压为最小值--本例为85V。
(2)设置输出负载为最大功率限定值。
(3)测量原边绕组P1的电流值,减小工作频率直到饱和开始(表示为在电流脉冲结束时有上翘)。在这些条件下增加的导通时间与平常导通时间之比的百分数,就是平常工作时磁通密度裕量的百分数。该裕量在磁通水平为高温时会降低(见图2.2.3),允许10%的超量以备磁心中的变化,加气隙尺寸及暂态要求。如果裕量不足,可增加气隙。
计算磁心饱和裕量
(1)使用伏秒方程,计算交流磁通Bac,最在最大负载和最小输入电压的输入功率下,计算或测量导通时间值及所加的电压,如下:
Bac=Vt/(NpAe)
在此,V=VCC,单位是V;
I=导通时间,单位是us;
NP=原边匝数;
Ae=磁心面积,单位是mm2;
Bac=交流峰值磁通密度,单位是T。
注意:要求磁通密度Bac是变化的以支持所施加的电压脉冲,并不包括任何DC成分。因此它与气隙尺寸无关。
实例
(2)使用螺线管方程和有效DC分量IDC(表示为导通初期电流的幅值),计算DC分量BDC。
假定磁心的所有磁阻都集中在气隙,那么将得到明显较高的DC磁通密度保守值。使用螺线管方程可得到其近似值。
在此,uo=4×10-7H/m
Np=原边匝数;
IDC=有效DC电流,单位是A;
a=气隙总长度,单位是mm;
BDC=DC磁通密度,单位是T。
实例
AC和DC磁通密度的叠加使磁心出现峰值。在1000C时再次检测磁心材料的特性。
实例
Bmax=Bac+BDC=205+103=308mT 最大值
电阻率高的 涡流损耗小 因此镍锌铁氧体可以工作在更高的频率上
磁导率
英文名称:magnetic permeability
表征磁介质磁性的物理量。常用符号μ表示,μ为介质的磁导率,或称绝对磁导率[1]。
μ等于磁介质中磁感应强度B与磁场强度H之比,即μ=B/H
通常使用的是磁介质的相对磁导率μr,其定义为磁导率μ与真空磁导率μ0之比,即μr=μ/μ0
相对磁导率μr与磁化率χ的关系是:μr=1+χ
磁导率μ,相对磁导率μr和磁化率xm都是描述磁介质磁性的物理量。
对于顺磁质μr>1;对于抗磁质μr<1,但两者的μr都与1相差无几 。在铁磁质中,B与 H 的关系是非线性的磁滞回线,μr不是常量,与H有关,其数值远大于1。
例如,如果空气(非磁性材料)的磁导率是1,则铁氧体的磁导率为10,000,即当比较时,以通过磁性材料的磁通密度是10,000倍。
涉及磁导率的公式:
磁场的能量密度=B^2/2μ
在国际单位制(SI)中,相对磁导率μr是无量纲的纯数,磁导率μ的单位是亨利/米(H/m)。
常用的真空磁导率
(1)初始磁导率μi:是指基本磁化曲线当H→0时的磁导率
公式
公式
(2)最大磁导率μm:在基本磁化曲线初始段以后,随着H的增大,斜率μ=B/H逐渐增大,到某一磁场强度下(Hm),磁密度达到最大值(Bm) ,即 公式
公式
(3)饱和磁导率μS:基本磁化曲线饱和段的磁导率,μs值一般很小,深度饱和时,μs=μo。
(4)差分(增量)磁导率μΔ∶μΔ=△B/△H。ΔB及△H是在(B1,H1)点所取的增量如图1和图2所示。
(5)微分磁导率,μd∶μd=dB /dH,在(B1,H1)点取微分,可得μd。
可知:μ1=B1/H1,μ△=△B /AH,μd=dB1/dH1,三者虽是在同一点上的磁导率,但在数值上是不相等的。
非磁性材料(如铝、木材、玻璃、自由空间)B与H之比为一个常数,用μ。来表示非磁性材料的的磁导率,即μ。=1(在CGS单位制中)或 μ。=4πX10o-7(在RMKS单位制中)。
在众多的材料中,如果自由空间(真空)的μo=1,那么比1略大的材料称为顺磁性材料(如白金、空气等);比1略小的材料,称为反磁性 材料(如银、铜、水等)。本章介绍的磁性元件μ》1是大有用处的。只有在需要磁屏蔽时,才会用铜等反磁性材料做成屏蔽罩使磁元件的磁 不会辐射到空间中去。
下面给出几个常用的参数式:
公式
公式
(1)有效磁导率μro。在用电感L形成闭合磁路中(漏磁可以忽略),磁心的有效磁导率为:
式中 L——绕组的自感量(mH);
W——绕组匝数;
磁心常数,是磁路长度Lm与磁心截面积Ae的比值(mm).
(2)饱和磁感应强度Bs。随着磁心中磁场强度H的增加,磁感应强度出现饱和时的B值,称为饱和磁感应强度B,。
(3)剩余磁感应强度Bs。磁心从磁饱和状态去除磁场后,剩余的磁感应强度(或称残留磁通密度)。
(4)矫顽力Hco。磁心从饱和状态去除磁场后,继续反向磁化,直至磁感应强度减小到零,此时的磁场强度称为矫顽力(或保磁力)。
公式
公式
(5)温度系数aμ°温度系数为温度在T1~T2范围内变化时,每变化1℃相应磁导率的相对变化量,即
式中 μr1——温度为T1时的磁导率;
μr2——温度为T2时的磁导率。
值得注意的是:除了磁导率μ与温度有关系之外,饱和磁感应强度BS、剩余磁感应强度BR、矫顽力HS,以及磁心比损耗(单位重量损耗W/kg)等磁参数,也都与磁心的工作温度有关。
真空磁导率是常数0.4*3.14*10-6,相对磁导率乘以真空磁导率就是实际的磁导率,不同的材质在不同的直流磁场H作用下,其相对磁导率对应一条非线性变化的曲线(H很大时,相对磁导率就会快速下降,降到很小的时候就可以认为饱和了),当H为0时的相对磁导率乘以真空磁导率就是初始磁导率。
当我要考虑变压器在工作时的励磁电流,那么我因该用H=NI/L计算出磁场强度,在用N*B*S=VIN*TON计算出磁通密度,再计算出此时的磁导率u=B/H,再根据磁阻计算出励磁电流。