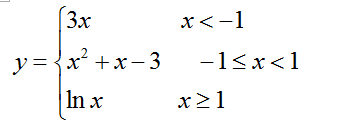Octave学习笔记
Octave是一款十分有用的数值计算软件。
一、Octave基础
1、使用Octave的内建函数
>> exp(1)
ans = 2.7183
说明:exp函数表示底数为e的指数函数。
>> x = 1.2*sin(40*pi/180+log(2.4^2))
x = 0.76618
说明:pi代表圆周率。
>> log(e)
ans = 1
>> log10(100)
ans = 2
>> sin(30*pi/180)
ans = 0.50000
求余函数:
>> rem(32,5)
ans = 2
>> rem(32,-5)
ans = 2
>> rem(-32,-5)
ans = -2
>> rem(-32,5)
ans = -2
平方根函数:
>> sqrt(4)
ans = 2
>> sqrt(-3)
ans = 0.00000 + 1.73205i
R语言不支持负数的平方根函数:
> sqrt(-3)
[1] NaN
Warning message:
In sqrt(-3) : 产生了NaNs
2、查看变量
>> who
Variables in the current scope:
ans x
3、清除变量
>> clear x
>> who
Variables in the current scope:
ans
4、支持复数运算
>> x = 3 + 2i
x = 3 + 2i
>> y = 4 - 5i
y = 4 - 5i
>> x + y
ans = 7 - 3i
>> x - y
ans = -1 + 7i
>> x * y
ans = 22 - 7i
>> x / y
ans = 0.048780 + 0.560976i
5、数据格式
>> format long
>> pi
ans = 3.14159265358979
>> format short
>> pi
ans = 3.1416
>>
6、无穷大
>> 10 / 0
warning: division by zero
ans = Inf
# Infinity
7、非数值
>> 0 / 0
warning: division by zero
ans = NaN
# Not a Number
8、误差问题
>> 1 - 0.2 - 0.2 - 0.2 - 0.2 - 0.2
ans = 5.5511e-017
9、载入和保存数据:
>> who
Variables in the current scope:
ans deg x y z
>> save myvar
>>
重启octave,此时,可使用以前定义的变量:
>> deg, x, y, z
deg = 0.017453
x = 2.3333
y = 2.3333
z = 2.3333
10、隐藏结果
>> x = sqrt(100)
;
>> x
x = 10
语句末尾加分号。
11、向量
>> a = [1 4 5]
a =
1 4 5
>> b = [3,4,5]
b =
3 4 5
>> c = [6;7;8]
c =
6
7
8
>> d = [c,9]
error: horizontal dimensions mismatch (3x1 vs 1x1)
>> d = [c;9]
d =
6
7
8
9
>> e = [b,6]
e =
3 4 5 6
12、冒号表达式
>> x = 5:10
x =
5 6 7 8 9 10
>> x = [100:0.5:105]
x =
Columns 1 through 6:
100.00 100.50 101.00 101.50 102.00 102.50
Columns 7 through 11:
103.00 103.50 104.00 104.50 105.00
13、大矩阵的显示
>> x = 1:1000
>> more off // 滚屏显示
>> more on // 分屏显示
14、向量构造函数
>> ones(4,5)
ans =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
>> zeros(3,4)
ans =
0 0 0 0
0 0 0 0
0 0 0 0
>> linspace(10,20,5)
ans =
10.000 12.500 15.000 17.500 20.000
>> logspace(1,3,5)
ans =
10.000 31.623 100.000 316.228 1000.000
>> a = [1:2:6 -1 0]
a =
1 3 5 -1 0
>> a(1)
ans = 1
>> a(2:4)
ans =
3 5 -1
>> a(1:2:5)
ans =
1 5 0
>> a(1:1:5)
ans =
1 3 5 -1 0
. —— 逐个元素进行运算
>> a = [1,2,3;4,5,6;7,8,9]
a =
1 2 3
4 5 6
7 8 9
>> a ^ 2
ans =
30 36 42
66 81 96
102 126 150
>> a.^2
ans =
1 4 9
16 25 36
49 64 81
15、绘制函数图像
>> angles = [0:pi/6:2*pi];
>> y = sin(angles);
>> plot(angles,y)
缺点:图像显得粗糙。
更加精确的图像:
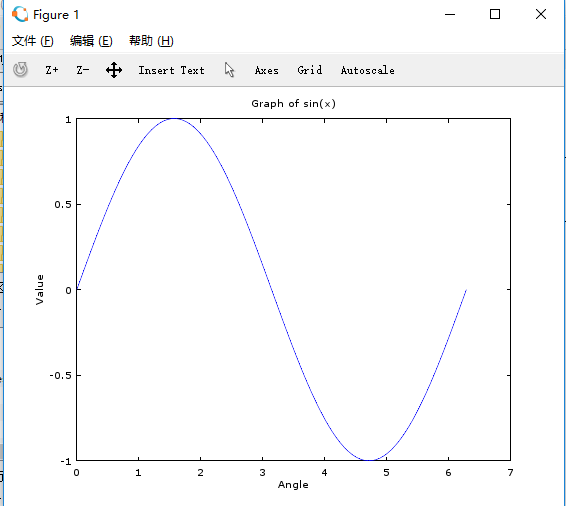
>> angles = linspace(0,2*pi,100);
>> y = sin(angles);
>> plot(angles,y);
改进该图像:
>> title("Graph of sin(x)")
>> xlabel("Angle")
>> ylabel("Value")
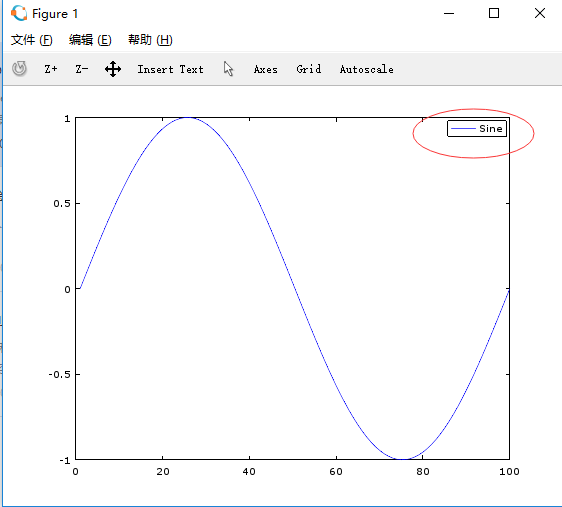
>> plot(y)
>> legend("Sine")
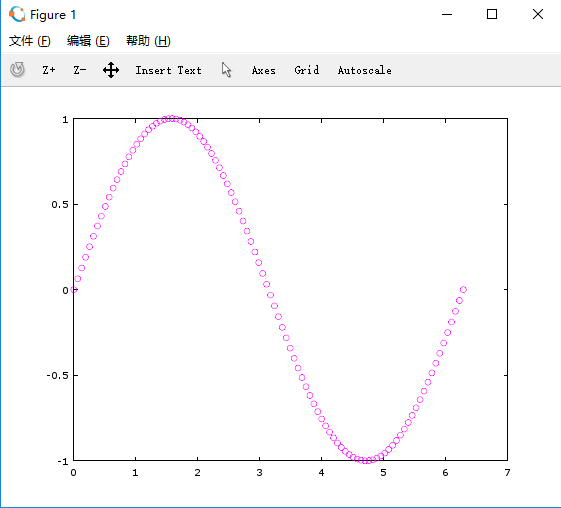
>> angles = linspace(0,2*pi,100);
>> y = sin(angles);
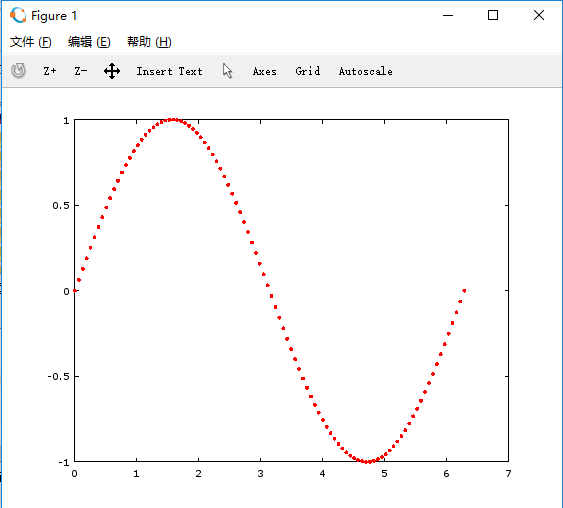
>> plot(angles,y,'r.')
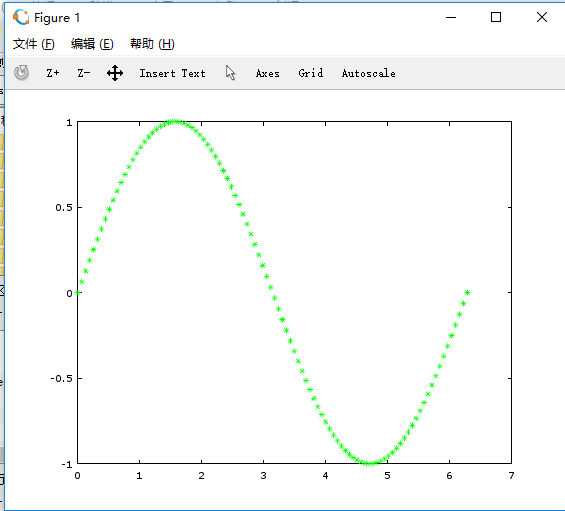
>> plot(angles,y,'g*')
>> plot(angles,y,'mo')
在R语言里:
> x <- seq(0,2*pi,by=pi/6)
> y <- sin(x)
> plot(x,y)
> lines(loess.smooth(x,y),col='red',lwd=2)
>
y <- function(x){sin(x)}
>
curve(y,0,2*pi)
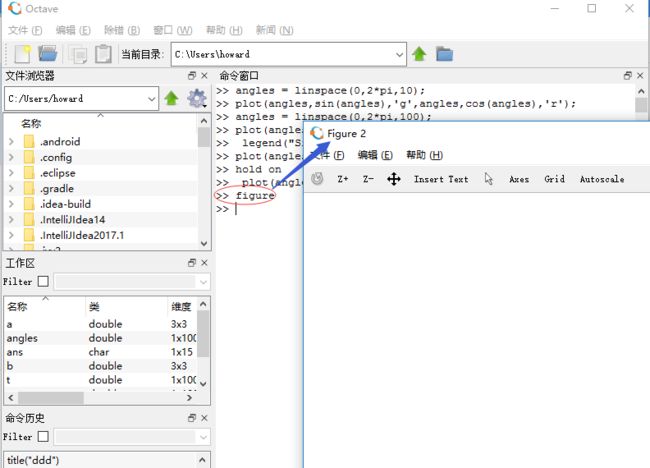
16、绘制多个图像
>> angles = linspace(0,2*pi,100);
>> plot(angles,sin(angles),'g',angles,cos(angles),'r');
>> legend("Sine","Cosine");
>> plot(angles,sin(angles),'g')
>> hold on
>> plot(angles,cos(angles),'r')
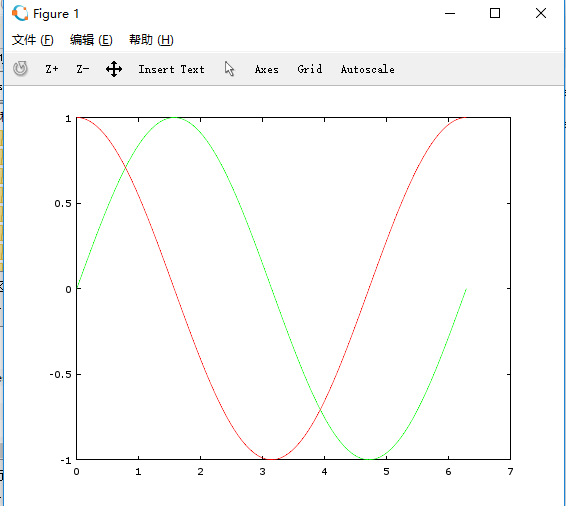
>>
hold off
二、Octave 编程I:脚本文件
如果你有一些重复输入的命令的,你可以将这一系列的命令存入一个Octave 脚本之中。这种包含Octave 命令的文本文件是Octave 程序的基本形式。当你在Octave 中执行这样的脚本的时候,其效果与将这些命令一行行输入Octave 中的效果是一样的。而且当你对一系列要输入Octave 的命令不是很拿的准的时候,在一个脚本中修改这些命令会比在Octave 终端中重新调出及修改命令要简单方便许多。Octave 的脚本是普通的文本文件,但是他们需要有一个.m 的后缀(e.g. run.m)。因此,它们通常也被称为M 文件。除去后缀的文件名部分是你在执行该命令时需要向Octave 终端输入的部分。
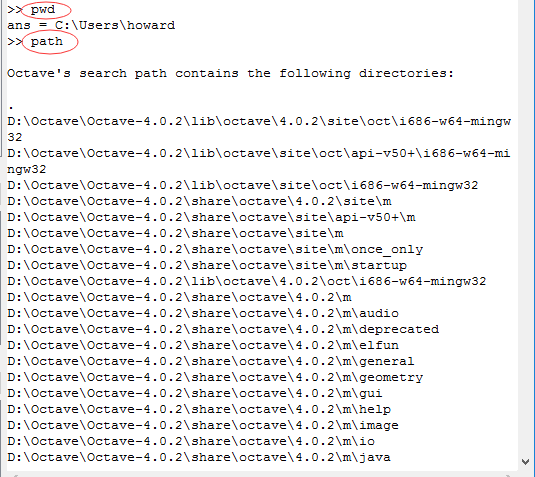
1、Path问题
添加路径,保存路径:
>> addpath("c:/windows/system32")
>> savepath
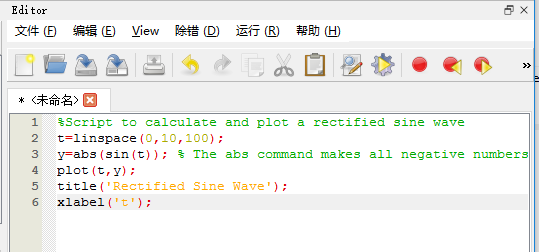
2、创建和编辑脚本
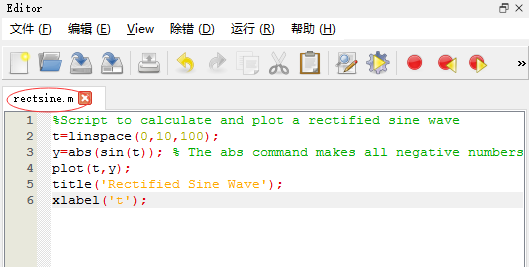
>> edit
保存文件:rectsine.m
3、运行脚本
4、记住之前的脚本
>>
what
M-files in directory C:\Users\howard:
myfunc.m rectsine.m
三、Octave控制结构
1、if语句
if expression
statements
elseif expression
statements
else
statements
end
>> pi > exp(1) & sqrt(-1) == i
ans = 1
>> 1 == 2
ans = 0
这与C++ 中的语法又一定的差异:Octave 中条件不需要用括号() 括起来(当然使用括号会让程序更加明了), 而且statments 程序块不需要用大括号{ } 括起来。另外,Octave 中需要用end 命令来标识if 语句的结束。在Octave 中,if...end 和if...endif 都是合法的。使用end 可以让Octave 的文件与Matlab 文件兼容。
>> age = 18;
>> if age > 18
msg = "welcome"
else
msg = "no way"
endif
msg = no way
2、switch语句
switch x
case x1
statements
case x2
statements
otherwise
statements
end
>> a = 1;
>> switch a
case 0
disp
("a is zero")
case 1
disp
("a is one")
otherwise
disp
("a is not a binary digit")
end
a is one
3、for循环
for variable=vector
statements
end
>> for n = 1:5
nf(n) = factorial(n);
end
>> disp(nf)
1 2 6 24 120
>> nf(5)
ans = 120
4、while循环
while expression
statements
end
>> x = 1;
>> while x + 1 > 1
x = x / 2;
end
>> x
x = 1.1102e-016
保存文件sindeg.m。
>> help sindeg
'sindeg' is a function from the file C:\Users\howard\sindeg.
sindeg(x) Calculate sine(x) in degrees
调用自定义函数sindeg:
>> sindeg(30)
>> sindeg(30)
ans = 0.50000
>> sindeg(60)
ans = 0.86603
>> sindeg(90)
ans = 1
>> sindeg([0 30 45 60 90])
ans =
0.00000 0.50000 0.70711 0.86603 1.00000
注意:向量[0 30 45 60 90] 等价于 [0,30,45,60,90]
>> sindeg([0, 30, 45, 60, 90])
ans =
0.00000 0.50000 0.70711 0.86603 1.00000
>> sindeg([0:15:90])
ans =
Columns 1 through 5:
0.00000
0.25882
0.50000
0.70711 0.86603
Columns 6 and 7:
0.96593
1.00000
五、矩阵
矩阵乘法:
>> A = [1 2; 4 5]
A =
1 2
4 5
>> B = [2 3;2 1]
B =
2 3
2 1
>> A*B // 矩阵乘法
ans =
6 5
18 17
>> A.*B // 逐个元素相乘
ans =
2 6
8 5
>> A = [1 2; 4 5]
A =
1 2
4 5
>> 2.^A
ans =
2 4
16 32
>> A.^2
ans =
1 4
16 25
矩阵转置:
>> A=[5 7 9;-1 3 -2]
A =
5 7 9
-1 3 -2
>> A'
ans =
5 -1
7 3
9 -2
矩阵创建函数
>>
ones(3,4) // 一矩阵
ans =
1 1 1 1
1 1 1 1
1 1 1 1
>>
zeros(3,4) // 零矩阵
ans =
0 0 0 0
0 0 0 0
0 0 0 0
>>
eye(4,4) // 单位矩阵
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> diag([5 7 -2 3]) // 对角矩阵
ans =
Diagonal Matrix
5 0 0 0
0 7 0 0
0 0 -2 0
0 0 0 3
>> A = [3 4 5;5 6 7;2 3 1]
A =
3 4 5
5 6 7
2 3 1
>> diag(A)
ans =
3
6
1
在R语言里如此操作:

创建复合矩阵:
>> A = [5 7 9; -1 3 2]
A =
5 7 9
-1 3 2
>> B = [2 0; 0 -1; 1 0]
B =
2 0
0 -1
1 0
>>
comp = [eye(3) B; A zeros(2,2)]
comp =
1 0 0 2 0
0 1 0 0 -1
0 0 1 1 0
5 7 9 0 0
-1 3 2 0 0
提取矩阵元:
>> J = [1 2 3 4;5 6 7 8;11 12 13 10]
J =
1 2 3 4
5 6 7 8
11 12 13 10
>> J(1,1)
ans = 1
>> J(2,3)
ans = 7
>> J(1:2,4)
ans =
4
8
>> J(3,:)
ans =
11 12 13 10
>> J(3,2:3)=[100 200]
J =
1 2 3 4
5 6 7 8
11 100 200 10
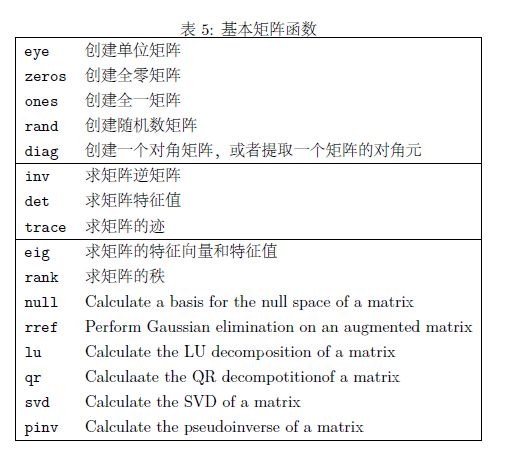
六、基本矩阵函数
>>
eye(3,3)
ans =
Diagonal Matrix
1 0 0
0 1 0
0 0 1
>>
zeros(3,4)
ans =
0 0 0 0
0 0 0 0
0 0 0 0
>>
ones(4,3)
ans =
1 1 1
1 1 1
1 1 1
1 1 1
>>
rand(3,4)
ans =
0.797171 0.590823 0.402968 0.054905
0.166635 0.999966 0.470865 0.015384
0.355731 0.608702 0.135199 0.527493
>>
diag([5 6 -2 3])
ans =
Diagonal Matrix
5 0 0 0
0 6 0 0
0 0 -2 0
0 0 0 3
>> A = [4 5 2;1 3 7;5 7 1]
A =
4 5 2
1 3 7
5 7 1
>>
inv(A)
ans =
1.53333 -0.30000 -0.96667
-1.13333 0.20000 0.86667
0.26667 0.10000 -0.23333
>> det(A)
ans = -30.000
在
线性代数
中,一个n×n矩阵A的
主对角线
(从左上方至右下方的对角线)上各个元素的总和被称为
矩阵
A的迹(或迹数),一般记作tr(A)。
>> trace(A)
ans = 8
数学上,线性变换的特征
向量
(本征向量)是一个非简并的向量,其方向在该变换下不变。该向量在此变换下缩放的比例称为其特征值(
本征值
)。一个线性变换通常可以由其特征值和特征向量完全
描述
。特征空间是相同特征值的特征向量的集合。“特征”一词来自德语的eigen。1904年希尔伯特首先在这个意义下使用了这个词,更早亥尔姆霍尔兹也在相关意义下使用过该词。
eigen
一词可翻译为”自身的”、“特定于……的”、“有特征的”、或者“个体的”。这显示了特征值对于定义特定的线性变换有多重要。
从数学上看,如果向量v与变换A满足 Av=λv
则称向量v是变换A的一个特征向量,λ是相应的特征值。其中是将变换作用于v得到的向量。这一等式被称作“特征值方程”。
没有搞清楚,待会儿查看线性代数教程,搞明白特征值和特征向量。
>>
eig(A)
ans =
11.64352
0.60627
-4.24980
矩阵的秩是线性代数中的一个概念。在线性代数中,一个矩阵A的列秩是A的线性独立的纵列的极大数。通常表示为r(A),rk(A)或rank A。
>> rank(A)
ans = 3
>> B = [1 2 3;2 4 6;5,6 2]
B =
1 2 3
2 4 6
5 6 2
>> det(B)
ans = 0
>> rank(B)
ans = 2
>> svd(A)
ans =
12.00696
5.88666
0.42444
>> pinv(A)
ans =
1.53333 -0.30000 -0.96667
-1.13333 0.20000 0.86667
0.26667 0.10000 -0.23333
>> lu(A)
ans =
5.00000 7.00000 1.00000
0.20000 1.60000 6.80000
0.80000 -0.37500 3.75000
>> qr(A)
ans =
-6.48074 -8.94959 -3.08607
0.15430 -1.70434 -6.09091
0.77152 0.20250 -2.71607
>> rref(A)
ans =
1 0 0
0 1 0
0 0 1
七、解决AX=B类问题
Octave 的画图功能不仅仅是画简单的二维直角坐标系下的曲线。通过调用GNUPLOT,它可以画出条形图,3D 表面,等高线图和极坐标图等等。
1、子图
要在同一个窗口中创建多幅图片通过subplot 命令实现。该命令能够将窗口分离成一系列的子窗口,其基本语法为subplot(row,columns,select)。其中subplot 参数指定当前绘图在子窗口中的序列。子窗口的序号按照从上到下,从左到右的次序递增。接下来用一个例子来说明subplot 的应用。
>> x = linspace(-10,10);
>> subplot(2,1,1);
>> plot(x,sin(x));
>> subplot(2,1,2);
>> plot(x,sin(x)./x);

>> x = linspace(-10,10);
>> subplot(2,2,1);
>> plot(x,x.^2+3*x-1);
>> subplot(2,2,2);
>> plot(x,sin(x));
>> subplot(2,2,3);
>> plot(x,cos(x));
>> subplot(2,2,4);
>> plot(x,exp(x));

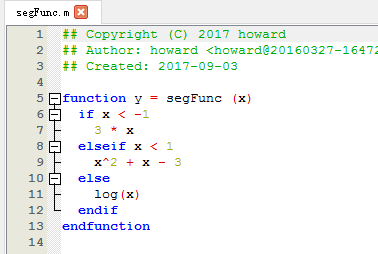
>> segFunc(-2)
ans = -6
>> segFunc(0)
ans = -3
>> segFunc(e)
ans = 1
调用函数计算都是没有问题的。但是绘制图像却不行。
>> x = linspace(-4,4);
>> plot(x,segFunc(x));

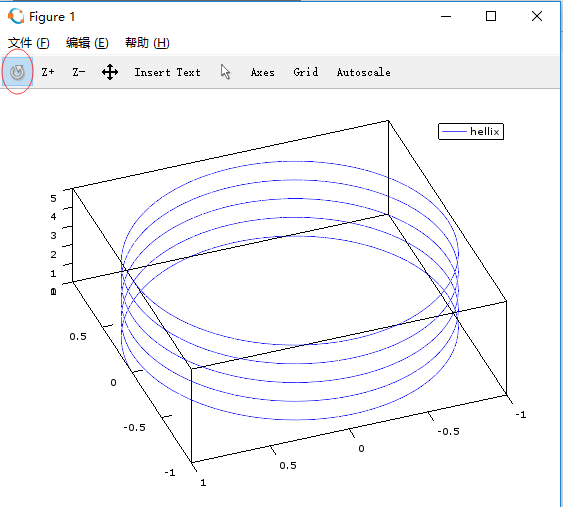
2、3D绘图
>> x = [0:0.01:5];
>> y = [0:0.01:5];
>> z = [0:0.01:5];
>> plot3(cos(2*pi*x),sin(2*pi*y),z,";hellix;")
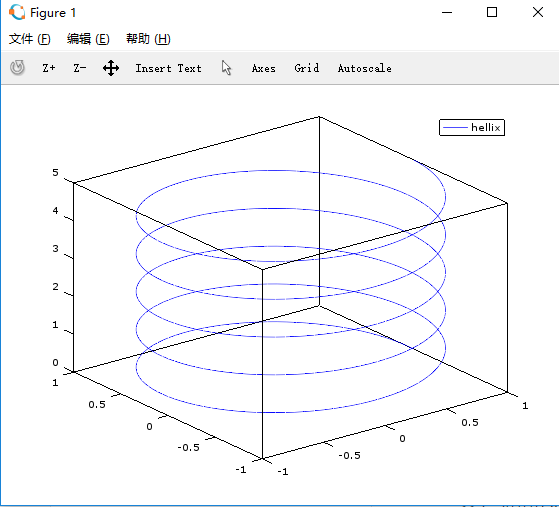
导入数据文件:

>> cd e:/software
>> dir
. eclipse
.. images
.RData job.txt
.Rhistory prices.txt
SelectApplicants.r redis2.6.12
costFunction.m spark-2.2.0-bin-hadoop2.7
descentFunction.m
>>
A = load("prices.txt")
A =
825.0000 135.0000 3.0000 2.0000
997.5000 133.0000 3.0000 2.0000
1005.0000 134.0000 3.0000 2.0000
384.0000 64.0000 3.0000 2.0000
270.0000 45.0000 2.0000 1.0000
459.6000 76.0000 1.0000 1.0000
388.8000 64.8000 1.0000 1.0000
713.4000 118.9000 1.0000 1.0000
218.4000 39.0000 1.0000 1.0000
1145.5000 145.0000 3.0000 2.0000
1864.4000 236.0000 4.0000 2.0000
539.0000 77.0000 2.0000 2.0000
679.0000 97.0000 3.0000 2.0000
756.0000 108.0000 3.0000 2.0000
784.0000 112.0000 3.0000 2.0000
487.5000 75.0000 1.0000 2.0000
780.0000 120.0000 2.0000 2.0000
780.0000 120.0000 2.0000 2.0000
780.0000 120.0000 3.0000 2.0000
995.5000 147.0000 3.0000 2.0000
1072.5000 165.0000 3.0000 2.0000
1072.5000 165.0000 3.0000 2.0000
导入图像文件:
对于图像文件,octave用imread将图像导入并存为矩阵img,
img = imread("file.png") ;
在octave里显示图像很简单,用命令:
imshow(img) ;
除了jpeg和png格式的图像可以直接导入,其他格式的图像必须经过ImageMagick的convert函数转换后才可读入。ImageMagick是命令行的强大的图像处理工具,convert几乎涵盖了所有格式图像的转换。
如果你关心imread函数的源码,可以去读 /usr/local/share/octave/packages/image-1.0.8/imread.m,该函数把灰度图像导入为MxN矩阵,把彩色图像导入为MxNx3矩阵。具体的帮助文件,可以
help imread ;
或者来个更详细点儿的
help -i imread ;