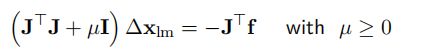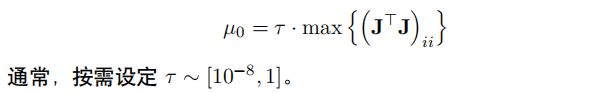[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析
长篇警告⚠⚠⚠
目录
- solver 全流程回顾
- Solver三要素
- Solver求解中的疑问
- 核心问题
- 代码解析
- 1. TestMonoBA.cpp
- 2. 后端部分:
- 2.1 顶点
- 2.2 边(残差)
- 2.2.1 边的框架
- 2.2.2 首先计算残差
- ① 视觉重投影残差
- ② IMU预积分残差
- 2.2.3 计算残差的雅可比
- ① `edge_reprojection.cc`视觉残差的雅可比
- ② IMU残差的雅可比矩阵
- 2.3 problem类
- 2.3.1 向problem中添加顶点
- 2.3.2 向problem中添加边
- 2.3.3 solve函数
- 2.3.3.1 统计优化变量的维数,为构建 H 矩阵做准备
- 2.3.3.2 通过MakeHessian()构建H矩阵
- 【补充】鲁棒核函数的H矩阵以及b
- 2.3.3.3 LM算法的初始化
- 2.3.3.4 LM算法基本流程
- 2.3.3.5 求解线性方程
- 2.3.3.6 更新状态量`UpdateStates()`:
- 2.3.3.7 判断当前步是否可行以及 LM 的 lambda 怎么更新
- 2.3.3.8 回滚操作
- 3. 边缘化的测试函数
solver 全流程回顾
Solver三要素
Solver求解中的疑问
- 信息矩阵 H 不满秩,那求解时如何操作?
• 使用 LM 算法,加阻尼因子使得系统满秩,可求解,但是求得的结果可能会往零空间变化。
• 添加先验约束,增加系统的可观性。比如 g2o tutorial 中对第一个pose 的信息矩阵加上单位阵 H[11]+ = I. - orbslam,svo 等求 mono BA 问题时,fix 一个相机 pose 和一个特征点,或者 fix 两个相机 pose,也是为了限定优化值不乱飘。那代码如何实现 fix 呢?
• 添加超强先验,使得对应的信息矩阵巨大(如,1015),就能使得∆x = 0;
• 设定对应雅克比矩阵为 0,意味着残差等于 0. 求解方程为(0 + λI) ∆x = 0,只能 ∆x = 0。
核心问题
代码解析
整个代码的结构如下:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第6张图片](http://img.e-com-net.com/image/info8/2db3fdaf86924709b256e665387c0cd1.jpg)
app放置应用问题的函数,例如这里是slam的BA问题,backend里涵盖后端的相应库函数,先看BA问题(TestMonoBA.cpp):
1. TestMonoBA.cpp
产生世界坐标系下的虚拟数据: 相机姿态, 特征点, 以及每帧观测
/*
* Frame : 保存每帧的姿态和观测
* */
struct Frame {
Frame(Eigen::Matrix3d R, Eigen::Vector3d t) : Rwc(R), qwc(R), twc(t) {};
Eigen::Matrix3d Rwc; //旋转矩阵
Eigen::Quaterniond qwc; //四元数表示的旋转和平移
Eigen::Vector3d twc; //平移向量
unordered_map<int, Eigen::Vector3d> featurePerId; // 该帧观测到的特征以及特征id};
/* * 产生世界坐标系下的虚拟数据: 相机姿态, 特征点, 以及每帧观测 */
void GetSimDataInWordFrame(vector<Frame> &cameraPoses, vector<Eigen::Vector3d> &points) {
int featureNums = 20; // 特征数目,假设每帧都能观测到所有的特征
int poseNums = 3; // 相机数目
double radius = 8;
for (int n = 0; n < poseNums; ++n) {
double theta = n * 2 * M_PI / (poseNums * 4); // 1/4 圆弧
// 绕 z轴 旋转
Eigen::Matrix3d R;
R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());
Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));
cameraPoses.push_back(Frame(R, t));
}
// 随机数生成三维特征点
std::default_random_engine generator; //创建随机数引擎
std::normal_distribution<double> noise_pdf(0., 1. / 1000.); // 2pixel / focal
for (int j = 0; j < featureNums; ++j) {
std::uniform_real_distribution<double> xy_rand(-4, 4.0); // 产生均匀分布的随机数,创建取值范围
std::uniform_real_distribution<double> z_rand(4., 8.);
Eigen::Vector3d Pw(xy_rand(generator), xy_rand(generator), z_rand(generator));
points.push_back(Pw); //产生世界坐标系中的特征点
// 在每一帧上的观测量
for (int i = 0; i < poseNums; ++i) {
Eigen::Vector3d Pc = cameraPoses[i].Rwc.transpose() * (Pw - cameraPoses[i].twc); //得到相机坐标系中的特征点
Pc = Pc / Pc.z(); // 归一化图像平面
Pc[0] += noise_pdf(generator); // 加噪声
Pc[1] += noise_pdf(generator);
cameraPoses[i].featurePerId.insert(make_pair(j, Pc)); // 三维特征点-帧特征点
}
}
}【注】相关函数的解析
uniform_real_distribution:浮点数均匀分布模板类,产生均匀分布的随机数,,可以用float和double来实例化。参数说明了随机数的范围:半开范围[ )
main主函数:
int main() {
// 准备数据
vector<Frame> cameras;
vector<Eigen::Vector3d> points;
GetSimDataInWordFrame(cameras, points);
Eigen::Quaterniond qic(1, 0, 0, 0);
Eigen::Vector3d tic(0, 0, 0);
// 构建 problem(最小二乘) Problem
problem(Problem::ProblemType::SLAM_PROBLEM);
// 所有 Pose
vector<shared_ptr<VertexPose> > vertexCams_vec;
for (size_t i = 0; i < cameras.size(); ++i) {
shared_ptr<VertexPose> vertexCam(new VertexPose());
Eigen::VectorXd pose(7); // 三维的平移+四维的四元数--6自由度
pose << cameras[i].twc, cameras[i].qwc.x(), cameras[i].qwc.y(),
cameras[i].qwc.z(), cameras[i].qwc.w();
vertexCam->SetParameters(pose);
// if(i < 2)
// vertexCam->SetFixed();
problem.AddVertex(vertexCam);
vertexCams_vec.push_back(vertexCam);
}
// 所有 Point 及 edge(残差)
std::default_random_engine generator;
std::normal_distribution<double> noise_pdf(0, 1.);
double noise = 0; vector<double> noise_invd;
vector<shared_ptr<VertexInverseDepth> > allPoints;
for (size_t i = 0; i < points.size(); ++i) {
//假设所有特征点的起始帧为第0帧, 逆深度容易得到
Eigen::Vector3d Pw = points[i];
Eigen::Vector3d Pc = cameras[0].Rwc.transpose() * (Pw - cameras[0].twc);
noise = noise_pdf(generator);
double inverse_depth = 1. / (Pc.z() + noise);
// double inverse_depth = 1. / Pc.z();
noise_invd.push_back(inverse_depth);
// 初始化特征 vertex
shared_ptr<VertexInverseDepth> verterxPoint(new VertexInverseDepth());
VecX inv_d(1);
inv_d << inverse_depth;
verterxPoint->SetParameters(inv_d);
problem.AddVertex(verterxPoint);
allPoints.push_back(verterxPoint);
// 每个特征点j对应的投影误差edge, 第 0 帧为起始帧
for (size_t j = 1; j < cameras.size(); ++j) {
Eigen::Vector3d pt_i = cameras[0].featurePerId.find(i)->second;
Eigen::Vector3d pt_j = cameras[j].featurePerId.find(i)->second;
shared_ptr<EdgeReprojection> edge(new EdgeReprojection(pt_i, pt_j));
edge->SetTranslationImuFromCamera(qic, tic);
std::vector<std::shared_ptr<Vertex> > edge_vertex;
edge_vertex.push_back(verterxPoint);
edge_vertex.push_back(vertexCams_vec[0]);
edge_vertex.push_back(vertexCams_vec[j]);
edge->SetVertex(edge_vertex);
problem.AddEdge(edge);
}
}
problem.Solve(5); // 求解,迭代5步
// 三维特征点,原始数据、加噪声后数据、优化后数据
std::cout << "\nCompare MonoBA results after opt..." << std::endl;
for (size_t k = 0; k < allPoints.size(); k+=1) {
std::cout << "after opt, point " << k << " : gt " << 1. / points[k].z() << " ,noise "
<< noise_invd[k] << " ,opt " << allPoints[k]->Parameters() << std::endl;
}
std::cout<<"------------ pose translation ----------------"<<std::endl;
for (int i = 0; i < vertexCams_vec.size(); ++i) {
std::cout<<"translation after opt: "<< i <<" :"<< vertexCams_vec[i]->Parameters().head(3).transpose() << " || gt: "<<cameras[i].twc.transpose()<<std::endl;
}
/// 优化完成后,第一帧相机的 pose 平移(x,y,z)不再是原点 0,0,0. 说明向零空间发生了漂移。
/// 解决办法: fix 第一帧和第二帧,固定 7 自由度。 或者加上非常大的先验值。 80、81 fix
problem.TestMarginalize();
return 0;
}
可以看到这里的顶点有verterxPose和vertexCam两种,分别代表特征点(逆深度)和相机位姿。
2. 后端部分:
2.1 顶点
顶点、边、求解器都有对应的文件,所有顶点对应的父类为vertex,它有一个VecX来表示它的值,然后还要指定其维度。以姿态的顶点VertexPose为例:
vertex_pose.h
/**
* Pose vertex * parameters: tx, ty, tz, qx, qy, qz, qw, 7 DoF
* optimization is perform on manifold, so update is 6 DoF, left multiplication
*
* pose is represented as Twb in VIO case
*/
class VertexPose : public Vertex {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
VertexPose() : Vertex(7, 6) {} // 传进7个,但只有六自由度的变量
/// 加法,可重定义
/// 默认是向量加
virtual void Plus(const VecX &delta) override;
std::string TypeInfo() const {
return "VertexPose";
}
};构造函数的两项参数为其变量的维数和实际自由度,比如姿态有6个自由度但是由于使用了四元数表示所以一共7维,这里就是7和6。同时对加法进行了override:
vertex_pose.cc
// 定义广义的加法void
VertexPose::Plus(const VecX &delta) {
VecX ¶meters = Parameters();
parameters.head<3>() += delta.head<3>();
Qd q(parameters[6], parameters[3], parameters[4], parameters[5]);
q = q * Sophus::SO3d::exp(Vec3(delta[3], delta[4], delta[5])).unit_quaternion(); // right multiplication with so3
q.normalized(); // 归一化操作
parameters[3] = q.x();
parameters[4] = q.y();
parameters[5] = q.z();
parameters[6] = q.w();
}平移部分直接相加,旋转部分需要先将四元数的虚部转换为SO3下的更新量,再右乘原来的四元数,得到更新后的四元数,之后对四元数进行了归一化。
2.2 边(残差)
边负责计算残差,残差=预测-观测,维度在构造函数中定义代价函数是 (残差×信息×残差),是一个数值,由后端求和后最小化。edge类的构造函数如下:
edge.h
/**
* 构造函数,会自动化配雅可比的空间
* @param residual_dimension 残差维度
* @param num_verticies 顶点数量
* @param verticies_types 顶点类型名称,可以不给,不给的话check中不会检查
*/
explicit Edge(int residual_dimension, int num_verticies, const std::vector<std::string> &verticies_types = std::vector<std::string>());
...
/// 计算残差,由子类实现
virtual void ComputeResidual() = 0;
/// 计算雅可比,由子类实现
/// 本后端不支持自动求导,需要实现每个子类的雅可比计算方法
virtual void ComputeJacobians() = 0;2.2.1 边的框架
框架:
edge_reprojection.h
/**
* 此边是视觉重投影误差,此边为三元边,与之相连的顶点有:
* 路标点的逆深度InveseDepth、第一次观测到该路标点的source Camera的位姿T_World_From_Body1,
* 和观测到该路标点的mearsurement Camera位姿T_World_From_Body2。
* 注意:verticies_顶点顺序必须为InveseDepth、T_World_From_Body1、T_World_From_Body2。
*/
class EdgeReprojection : public Edge {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
EdgeReprojection(const Vec3 &pts_i, const Vec3 &pts_j)
: Edge(2, 3, std::vector<std::string>{"VertexInverseDepth", "VertexPose", "VertexPose"}) {
pts_i_ = pts_i;
pts_j_ = pts_j;
}
/// 返回边的类型信息
virtual std::string TypeInfo() const override { return "EdgeReprojection"; }
/// 计算残差
virtual void ComputeResidual() override;
/// 计算雅可比
virtual void ComputeJacobians() override;
void SetTranslationImuFromCamera(Eigen::Quaterniond &qic_, Vec3 &tic_);
private:
//Translation imu from camera
Qd qic;
Vec3 tic;
//measurements
Vec3 pts_i_, pts_j_;
};
/**
* 此边是视觉重投影误差,此边为二元边,与之相连的顶点有:
* 路标点的世界坐标系XYZ、观测到该路标点的 Camera 的位姿T_World_From_Body1
* 注意:verticies_顶点顺序必须为 XYZ、T_World_From_Body1
*/
class EdgeReprojectionXYZ : public Edge {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
EdgeReprojectionXYZ(const Vec3 &pts_i)
: Edge(2, 2, std::vector<std::string>{"VertexXYZ", "VertexPose"}) {
obs_ = pts_i;
}
/// 返回边的类型信息
virtual std::string TypeInfo() const override { return "EdgeReprojectionXYZ"; }
/// 计算残差
virtual void ComputeResidual() override;
/// 计算雅可比
virtual void ComputeJacobians() override;
void SetTranslationImuFromCamera(Eigen::Quaterniond &qic_, Vec3 &tic_);
private:
//Translation imu from camera
Qd qic;
Vec3 tic;
//measurements
Vec3 obs_;
};这里传入的pts_i和pts_j,分别是当前观测和下一帧观测的重投影的像素坐标,并且在归一化平面上,即z=1。前面说到edge要负责计算出顶点残差和其对应的雅克比,这部分的函数如下:
edge_reprojection.cc
2.2.2 首先计算残差
① 视觉重投影残差
这里的残差是按照第三讲中的视觉重投影误差计算的,首先取得i帧下的逆深度,然后获得两帧相机的姿态,之后通过坐标系的转换将i帧下的像素点坐标pts_i_转换到j帧的坐标系下,最后将转换过来的像素坐标(pts_camera_j / dep_j)和j帧下的测量值取差得到残差。
【强调】verticies_顶点顺序确定为InveseDepth、T_World_From_Body1、T_World_From_Body2。
/* std::vector> verticies_; // 该边对应的顶点
VecX residual_; // 残差
std::vector jacobians_; // 雅可比,每个雅可比维度是 residual x vertex[i]
MatXX information_; // 信息矩阵
VecX observation_; // 观测信息
*/
void EdgeReprojection::ComputeResidual() { // 残差的计算
double inv_dep_i = verticies_[0]->Parameters()[0]; // 逆深度
VecX param_i = verticies_[1]->Parameters(); // T_World_From_Body1
Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]);
Vec3 Pi = param_i.head<3>();
VecX param_j = verticies_[2]->Parameters(); // T_World_From_Body2
Qd Qj(param_j[6], param_j[3], param_j[4], param_j[5]);
Vec3 Pj = param_j.head<3>();
// 公式(61)的实现
Vec3 pts_camera_i = pts_i_ / inv_dep_i; // 对当前观测i的重投影的像素坐标归一化
Vec3 pts_imu_i = qic * pts_camera_i + tic; // i帧到imu-i的转换
Vec3 pts_w = Qi * pts_imu_i + Pi; // imu-i到world的转换
Vec3 pts_imu_j = Qj.inverse() * (pts_w - Pj); // world到imu-j的转换
Vec3 pts_camera_j = qic.inverse() * (pts_imu_j - tic); // imu-j到j帧的转换 fc_j
double dep_j = pts_camera_j.z();
residual_ = (pts_camera_j / dep_j).head<2>() - pts_j_.head<2>(); /// J^t * J * delta_x = - J^t * r
// residual_ = information_ * residual_; // remove information here, we multi information matrix in problem solver
}【相关知识点】
- 视觉残差为:
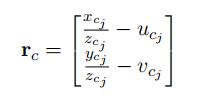
其中, u c i , v c i u_{c_i},v_{c_i} uci,vci指的是代码中传入的pts_i:当前观测的重投影的像素坐标。为求解视觉残差,则需要求解对于第 i 帧中的特征点,它投影到第 j 帧相机坐标系下的值,其计算公式为:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第8张图片](http://img.e-com-net.com/image/info8/2c3cbc2248074d0b8a0531e7d3b1d5b8.jpg)
推导各类 Jacobian 之前,为了简化公式,先定义如下变量(即为代码中的求解过程):
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第9张图片](http://img.e-com-net.com/image/info8/23d9c5de241f405db24a7e0d4f865048.jpg)
求解出 x c j x_{c_j} xcj, y c j y_{c_j} ycj, z c j z_{c_j} zcj代入残差公式即可求。
② IMU预积分残差
void EdgeImu::ComputeResidual()
{
VecX param_0 = verticies_[0]->Parameters();
Qd Qi(param_0[6], param_0[3], param_0[4], param_0[5]);
Vec3 Pi = param_0.head<3>();
VecX param_1 = verticies_[1]->Parameters();
Vec3 Vi = param_1.head<3>();
Vec3 Bai = param_1.segment(3, 3);
Vec3 Bgi = param_1.tail<3>();
VecX param_2 = verticies_[2]->Parameters();
Qd Qj(param_2[6], param_2[3], param_2[4], param_2[5]);
Vec3 Pj = param_2.head<3>();
VecX param_3 = verticies_[3]->Parameters();
Vec3 Vj = param_3.head<3>();
Vec3 Baj = param_3.segment(3, 3);
Vec3 Bgj = param_3.tail<3>()
residual_ = pre_integration_->evaluate(Pi, Qi, Vi, Bai, Bgi,
Pj, Qj, Vj, Baj, Bgj); // 计算IMU残差
SetInformation(pre_integration_->covariance.inverse());} // 得到IMU信息矩阵关于IMU残差计算evaluate()函数的详细代码解析和相关知识点可见我的另一篇博客——IMU预积分的第5节。
2.2.3 计算残差的雅可比
① edge_reprojection.cc视觉残差的雅可比
此代码的雅可比计算为视觉误差对两个时刻(i,j)的状态量以及逆深度的求导,没有涉及对imu与imu之间参数的求导。根据链式法则,雅可比的计算可以分两步走,第一步是误差对 f c j f_{c_j} fcj的求导(对应代码中的reduce),第二步是 f c j f_{c_j} fcj对各状态量的求导。详细解析已经在代码中注释。前面计算逆深度、各个变换矩阵的过程和计算残差与2.2.2相同.
void EdgeReprojection::ComputeJacobians() {
double inv_dep_i = verticies_[0]->Parameters()[0]; // 目标点逆深度的参数化1维
VecX param_i = verticies_[1]->Parameters();
Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]); // 第i时刻相机的POse
Vec3 Pi = param_i.head<3>(); // 第i时刻相机的平移
VecX param_j = verticies_[2]->Parameters();
Qd Qj(param_j[6], param_j[3], param_j[4], param_j[5]); // 第j时刻
Vec3 Pj = param_j.head<3>();
// 公式(61)的实现 对于第 i 帧中的特征点,它投影到第 j 帧相机坐标系下的值
Vec3 pts_camera_i = pts_i_ / inv_dep_i; // 对当前观测i的重投影的像素坐标归一化
Vec3 pts_imu_i = qic * pts_camera_i + tic;
Vec3 pts_w = Qi * pts_imu_i + Pi;
Vec3 pts_imu_j = Qj.inverse() * (pts_w - Pj);
Vec3 pts_camera_j = qic.inverse() * (pts_imu_j - tic); // fc_j = [xc_j,yc_j,zc_j]
double dep_j = pts_camera_j.z();
// 四元数变成矩阵
Mat33 Ri = Qi.toRotationMatrix(); // imu-i到world的转换
Mat33 Rj = Qj.toRotationMatrix(); // imu-j到world的转换
Mat33 ric = qic.toRotationMatrix(); // 相机到imu的转换
// 视觉误差对pts_camera_j求导
Mat23 reduce(2, 3);
// 公式(63)的实现
reduce << 1. / dep_j, 0, -pts_camera_j(0) / (dep_j * dep_j),
0, 1. / dep_j, -pts_camera_j(1) / (dep_j * dep_j);
// reduce = information_ * reduce;
Eigen::Matrix<double, 2, 6> jacobian_pose_i;
Eigen::Matrix<double, 3, 6> jaco_i;
// 公式(64)实现 fc_j对i时刻位移的求导 放置到jaco_i的左3列
jaco_i.leftCols<3>() = ric.transpose() * Rj.transpose();
// 公式(67)实现 fc_j对i时刻角度增量的求导 放置到jaco_i的右3列
jaco_i.rightCols<3>() = ric.transpose() * Rj.transpose() * Ri * -Sophus::SO3d::hat(pts_imu_i); // hat为向量到其对应的反对称矩阵 imu到相机的转换
// 公式(62)的部分实现——视觉误差对i时刻状态量的求导
jacobian_pose_i.leftCols<6>() = reduce * jaco_i;
Eigen::Matrix<double, 2, 6> jacobian_pose_j;
Eigen::Matrix<double, 3, 6> jaco_j;
// 公式(68)实现 fc_j对j时刻位移的求导 放置到jaco_j的左3列
jaco_j.leftCols<3>() = ric.transpose() * -Rj.transpose();
// 公式(70)实现 fc_j对j时刻角度增量的求导 放置到jaco_j的右3列
jaco_j.rightCols<3>() = ric.transpose() * Sophus::SO3d::hat(pts_imu_j);
// 公式(62)的部分实现——视觉误差对j时刻状态量的求导
jacobian_pose_j.leftCols<6>() = reduce * jaco_j;
Eigen::Vector2d jacobian_feature;
// 公式(76)的实现——视觉误差对特征逆深度的求导
jacobian_feature = reduce * ric.transpose() * Rj.transpose() * Ri * ric * pts_i_ * -1.0 / (inv_dep_i * inv_dep_i);
Eigen::Matrix<double, 2, 6> jacobian_ex_pose;
Eigen::Matrix<double, 3, 6> jaco_ex;
// 视觉误差对相机与imu之间的外参的求导
// 对位移的求导--公式(71)的实现
jaco_ex.leftCols<3>() = ric.transpose() * (Rj.transpose() * Ri - Eigen::Matrix3d::Identity());
// 对角度增量的求导
Eigen::Matrix3d tmp_r = ric.transpose() * Rj.transpose() * Ri * ric;
jaco_ex.rightCols<3>() = -tmp_r * Utility::skewSymmetric(pts_camera_i) + Utility::skewSymmetric(tmp_r * pts_camera_i) +// 公式(74)
Utility::skewSymmetric(ric.transpose() * (Rj.transpose() * (Ri * tic + Pi - Pj) - tic)); //公式(75)
jacobian_ex_pose.leftCols<6>() = reduce * jaco_ex;
// 雅可比矩阵
jacobians_[0] = jacobian_feature;
jacobians_[1] = jacobian_pose_i;
jacobians_[2] = jacobian_pose_j;
jacobians_[3] = jacobian_ex_pose;.【注】相关函数的解析
- Matrix3d M_so3_V1 = Sophus ::SO3 ::hat (so3_V1); //hat为向量到其对应的反对称矩阵
P.leftCols() // P(:, 1:cols) //前cols列
P.leftCols(cols) // P(:, 1:cols) //前cols列
P.middleCols(j) // P(:, j+1:j+cols) //中间cols列
P.middleCols(j, cols) // P(:, j+1:j+cols) //中间cols列
P.rightCols() // P(:, end-cols+1:end) //后cols列
P.rightCols(cols) // P(:, end-cols+1:end) //后cols列
参考资料
【相关知识点】
- 前文已经求解的
对于第i帧中的特征点,投影到第j帧相机坐标系下的三维坐标形式:
-
雅可比矩阵的形式:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第11张图片](http://img.e-com-net.com/image/info8/363dfa0737c8459a920d90b491954291.jpg)
分别表示视觉误差对 i i i时刻的状态量(平移、旋转),对 j j j时刻的状态量,对相机与Imu之间的外参,对逆深度的求导。 -
根据链式法则,Jacobian 的计算可以分两步走,第一步误差对 f c j f_{c_j} fcj 求导,求解公式如下:
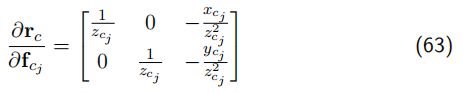
-
第二步 f c j f_{c_j} fcj 对各状态量求导:
(1) 对 i 时刻的状态量求导
a. 对 i 时刻位移求导,丢掉与平移无关的量(旋转部分),得到:![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第12张图片](http://img.e-com-net.com/image/info8/f78433c82f184a908e91cf21d3415ad5.jpg)
对i时刻位移求导有:

b. 对 i 时刻角度增量求导
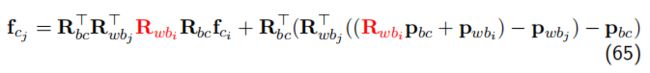 为简化,直接丢掉不相关的部分:
为简化,直接丢掉不相关的部分:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第13张图片](http://img.e-com-net.com/image/info8/ab60ec6d388740faab73026f6d466c75.jpg)
雅可比矩阵为:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第14张图片](http://img.e-com-net.com/image/info8/f55eda4380684f0ca8cf2a398a69ebea.jpg)
(2)对 j 时刻的状态量求导(原理同1类似)
a. 对位移求导: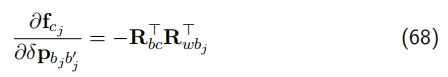
b. 对角度增量求导,同上,简化公式,去掉无关量:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第15张图片](http://img.e-com-net.com/image/info8/bc01b00371074d1598f292191f6d8f2e.jpg)
则雅可比矩阵为:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第16张图片](http://img.e-com-net.com/image/info8/bc3b2d181a9e4fb5b9f0538b2e295446.jpg)
(3)视觉误差对相机与imu之间的外参的求导
a.对位移的求导
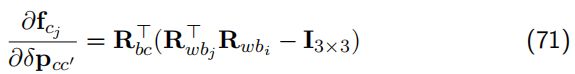
b.对角度增量求导,加式两部分都与 R b c R_{bc} Rbc有关,比较复杂,所以分两部分求导,这里只给出两部分求导的结果,两部分相加就是视觉误差对外参中的角度增量的最终结果。
①第一部分的雅可比:
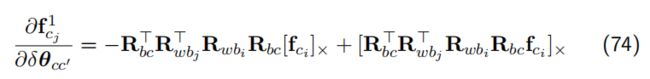 ②第二部分的雅可比(结果是一个反对称矩阵):
②第二部分的雅可比(结果是一个反对称矩阵):
(4)视觉误差对特征逆深度的求导,很容易:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第18张图片](http://img.e-com-net.com/image/info8/4981609226a24644914e4507cb116708.jpg)
将以上四部分整合进一个矩阵,最后得到整个视觉重投影误差的雅克比矩阵。
② IMU残差的雅可比矩阵
IMU残差的雅可比矩阵可以分为四个部分,分别是残差 r p 、 r q 、 r v r_p、r_q、r_v rp、rq、rv分别对状态量 R i R_i Ri、 p i p_i pi的一阶导、对状态量 R j R_j Rj、 p j p_j pj的一阶导、以及对两个时刻的速度和偏置的一阶导。
残差:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第19张图片](http://img.e-com-net.com/image/info8/a969b93781c44a658235e4a4b86dcba7.jpg)
状态量:
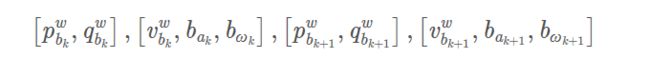
具体求解过程可参考博客——后端非线性优化中的第三部分-IMU约束。
EdgeImu::ComputeJacobians()详细代码略。
2.3 problem类
该类函数较多,所以从主函数用到的顺序来看,Problem problem(Problem::ProblemType::SLAM_PROBLEM);problem框架:
problem.h
class Problem {
public:
/**
* 问题的类型
* SLAM问题还是通用的问题
*
* 如果是SLAM问题那么pose和landmark是区分开的,Hessian以稀疏方式存储
* SLAM问题只接受一些特定的Vertex和Edge
* 如果是通用问题那么hessian是稠密的,除非用户设定某些vertex为marginalized
*/
enum class ProblemType {
SLAM_PROBLEM,
GENERIC_PROBLEM
};
typedef unsigned long ulong;
// typedef std::unordered_map> HashVertex;
typedef std::map<unsigned long, std::shared_ptr<Vertex>> HashVertex;
typedef std::unordered_map<unsigned long, std::shared_ptr<Edge>> HashEdge;
typedef std::unordered_multimap<unsigned long, std::shared_ptr<Edge>> HashVertexIdToEdge
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
Problem(ProblemType problemType);
~Problem();
bool AddVertex(std::shared_ptr<Vertex> vertex);
/**
* remove a vertex
* @param vertex_to_remove
*/
bool RemoveVertex(std::shared_ptr<Vertex> vertex);
bool AddEdge(std::shared_ptr<Edge> edge);
bool RemoveEdge(std::shared_ptr<Edge> edge);
/**
* 取得在优化中被判断为outlier部分的边,方便前端去除outlier
* @param outlier_edges
*/
void GetOutlierEdges(std::vector<std::shared_ptr<Edge>> &outlier_edges);
/**
* 求解此问题
* @param iterations
* @return
*/
bool Solve(int iterations);
/// 边缘化一个frame和以它为host的landmark
bool Marginalize(std::shared_ptr<Vertex> frameVertex,
const std::vector<std::shared_ptr<Vertex>> &landmarkVerticies);
bool Marginalize(const std::shared_ptr<Vertex> frameVertex);
//test compute prior
void TestMarginalize();
private:
/// Solve的实现,解通用问题
bool SolveGenericProblem(int iterations);
/// Solve的实现,解SLAM问题
bool SolveSLAMProblem(int iterations);
/// 设置各顶点的ordering_index
void SetOrdering();
/// set ordering for new vertex in slam problem
void AddOrderingSLAM(std::shared_ptr<Vertex> v);
/// 构造大H矩阵
void MakeHessian();
/// schur求解SBA
void SchurSBA();
/// 解线性方程
void SolveLinearSystem();
/// 更新状态变量
void UpdateStates();
void RollbackStates(); // 有时候 update 后残差会变大,需要退回去,重来
/// 计算并更新Prior部分
void ComputePrior();
/// 判断一个顶点是否为Pose顶点
bool IsPoseVertex(std::shared_ptr<Vertex> v);
/// 判断一个顶点是否为landmark顶点
bool IsLandmarkVertex(std::shared_ptr<Vertex> v);
/// 在新增顶点后,需要调整几个hessian的大小
void ResizePoseHessiansWhenAddingPose(std::shared_ptr<Vertex> v);
/// 检查ordering是否正确
bool CheckOrdering();
void LogoutVectorSize();
/// 获取某个顶点连接到的边
std::vector<std::shared_ptr<Edge>> GetConnectedEdges(std::shared_ptr<Vertex> vertex);
/// Levenberg
/// 计算LM算法的初始Lambda
void ComputeLambdaInitLM();
/// Hessian 对角线加上或者减去 Lambda
void AddLambdatoHessianLM();
void RemoveLambdaHessianLM();
/// LM 算法中用于判断 Lambda 在上次迭代中是否可以,以及Lambda怎么缩放
bool IsGoodStepInLM();
/// PCG 迭代线性求解器
VecX PCGSolver(const MatXX &A, const VecX &b, int maxIter);
double currentLambda_;
double currentChi_;
double stopThresholdLM_; // LM 迭代退出阈值条件
double ni_; //控制 Lambda 缩放大小
ProblemType problemType_;
/// 整个信息矩阵
MatXX Hessian_;
VecX b_;
VecX delta_x_;
/// 先验部分信息
MatXX H_prior_;
VecX b_prior_;
MatXX Jt_prior_inv_;
VecX err_prior_;
/// SBA的Pose部分
MatXX H_pp_schur_;
VecX b_pp_schur_;
// Heesian 的 Landmark 和 pose 部分
MatXX H_pp_;
VecX b_pp_;
MatXX H_ll_;
VecX b_ll_;
/// all vertices
HashVertex verticies_;
/// all edges
HashEdge edges_;
/// 由vertex id查询edge
HashVertexIdToEdge vertexToEdge_;
/// Ordering related
ulong ordering_poses_ = 0;
ulong ordering_landmarks_ = 0;
ulong ordering_generic_ = 0;
std::map<unsigned long, std::shared_ptr<Vertex>> idx_pose_vertices_; // 以ordering排序的pose顶点
std::map<unsigned long, std::shared_ptr<Vertex>> idx_landmark_vertices_; // 以ordering排序的landmark顶点
// verticies need to marg.
HashVertex verticies_marg_;
bool bDebug = false;
double t_hessian_cost_ = 0.0;
double t_PCGsovle_cost_ = 0.0;};2.3.1 向problem中添加顶点
problem.cc
bool Problem::AddVertex(std::shared_ptr<Vertex> vertex) {
if (verticies_.find(vertex->Id()) != verticies_.end()) {
// LOG(WARNING) << "Vertex " << vertex->Id() << " has been added before";
return false;
} else {
verticies_.insert(pair<unsigned long,shared_ptr<Vertex>>(vertex->Id(), vertex));
}
if (problemType_ == ProblemType::SLAM_PROBLEM) {
if (IsPoseVertex(vertex)) { // 判断一个顶点是否为Pose顶点
ResizePoseHessiansWhenAddingPose(vertex); // 在新增顶点后,需要调整几个hessian的大小
}
}
return true;
}
// 在新增顶点后,需要调整几个hessian的大小
void Problem::ResizePoseHessiansWhenAddingPose(shared_ptr<Vertex> v) {
int size = H_prior_.rows() + v->LocalDimension();
H_prior_.conservativeResize(size, size);
b_prior_.conservativeResize(size);
b_prior_.tail(v->LocalDimension()).setZero();
H_prior_.rightCols(v->LocalDimension()).setZero();
H_prior_.bottomRows(v->LocalDimension()).setZero();
}
// 判断一个顶点是否为Pose顶点
bool Problem::IsPoseVertex(std::shared_ptr<myslam::backend::Vertex> v) {
string type = v->TypeInfo();
return type == string("VertexPose");
}以添加顶点为例,函数会给顶点添加一个序号,同时根据顶点是否为pose来生成H矩阵,例如第一个pose在左上角0X0位置,第二个应该左上角就为6X6。
2.3.2 向problem中添加边
problem.cc
bool Problem::AddEdge(shared_ptr<Edge> edge) {
if (edges_.find(edge->Id()) == edges_.end()) {
edges_.insert(pair<ulong, std::shared_ptr<Edge>>(edge->Id(), edge));
} else {
// LOG(WARNING) << "Edge " << edge->Id() << " has been added before!";
return false; }
for (auto &vertex: edge->Verticies()) {
vertexToEdge_.insert(pair<ulong, shared_ptr<Edge>>(vertex->Id(), edge)); // 由vertex id查询edge
}
return true;
}2.3.3 solve函数
添加完顶点和边后,主函数直接调用solve方法problem.Solve(5);就结束了.
bool Problem::Solve(int iterations) {
if (edges_.size() == 0 || verticies_.size() == 0) {
std::cerr << "\nCannot solve problem without edges or verticies" << std::endl;
return false;
}
TicToc t_solve;
// 统计优化变量的维数,为构建 H 矩阵做准备
SetOrdering();
// 遍历edge, 构建 H 矩阵
MakeHessian();
// LM 初始化
ComputeLambdaInitLM();
// LM 算法迭代求解
bool stop = false;
int iter = 0;
while (!stop && (iter < iterations)) {
std::cout << "iter: " << iter << " , chi= " << currentChi_ << " , Lambda= " << currentLambda_ << std::endl;
bool oneStepSuccess = false;
int false_cnt = 0;
while (!oneStepSuccess) // 不断尝试 Lambda, 直到成功迭代一步
{
// setLambda
// AddLambdatoHessianLM();
// 第四步,解线性方程
SolveLinearSystem(); // 阻尼项在此
//
// RemoveLambdaHessianLM();
// 优化退出条件1: delta_x_ 很小则退出
if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {
stop = true;
break;
}
// 更新状态量
UpdateStates();
// 判断当前步是否可行以及 LM 的 lambda 怎么更新
oneStepSuccess = IsGoodStepInLM();
// 后续处理,
if (oneStepSuccess) {
// 在新线性化点 构建 hessian
MakeHessian();
// TODO:: 这个判断条件可以丢掉,条件 b_max <= 1e-12 很难达到,这里的阈值条件不应该用绝对值,而是相对值
// double b_max = 0.0;
// for (int i = 0; i < b_.size(); ++i) {
// b_max = max(fabs(b_(i)), b_max);
// }
// // 优化退出条件2: 如果残差 b_max 已经很小了,那就退出
// stop = (b_max <= 1e-12);
false_cnt = 0;
} else {
false_cnt ++;
RollbackStates(); // 误差没下降,回滚
}
}
iter++;
// 优化退出条件3: currentChi_ 跟第一次的chi2相比,下降了 1e6 倍则退出
if (sqrt(currentChi_) <= stopThresholdLM_)
stop = true;
}
std::cout << "problem solve cost: " << t_solve.toc() << " ms" << std::endl;
std::cout << " makeHessian cost: " << t_hessian_cost_ << " ms" << std::endl;
return true;
}2.3.3.1 统计优化变量的维数,为构建 H 矩阵做准备
void Problem::SetOrdering() {
// 每次重新计数
ordering_poses_ = 0;
ordering_generic_ = 0;
ordering_landmarks_ = 0;
int debug = 0;
// Note:: verticies_ 是 map 类型的, 顺序是按照 id 号排序的
for (auto vertex: verticies_) {
ordering_generic_ += vertex.second->LocalDimension(); // 所有的优化变量总维数
if (IsPoseVertex(vertex.second)) {
debug += vertex.second->LocalDimension();
}
if (problemType_ == ProblemType::SLAM_PROBLEM) // 如果是 slam 问题,还要分别统计 pose 和 landmark 的维数,后面会对他们进行排序
{
AddOrderingSLAM(vertex.second); // set ordering for new vertex in slam problem
}
if (IsPoseVertex(vertex.second)) {
std::cout << vertex.second->Id() << " order: " << vertex.second->OrderingId() << std::endl;
}
}
std::cout << "\n ordered_landmark_vertices_ size : " << idx_landmark_vertices_.size() << std::endl;
if (problemType_ == ProblemType::SLAM_PROBLEM) {
// 这里要把 landmark 的 ordering 加上 pose 的数量,就保持了 landmark 在后,而 pose 在前
ulong all_pose_dimension = ordering_poses_;
for (auto landmarkVertex : idx_landmark_vertices_) {
landmarkVertex.second->SetOrderingId(
landmarkVertex.second->OrderingId() + all_pose_dimension
);
}
}
// CHECK_EQ(CheckOrdering(), true);
}2.3.3.2 通过MakeHessian()构建H矩阵
遍历所有的edge的代码内部构建H矩阵的过程,对于每一条边都要进行这样两个for循环,分别是遍历方阵H的行和列,第一个i的for循环是行数,当遍历到行列相等,也就是对角的时候,只用放入一次hessian,而其他情况下都要放入关于对角对称的两个hessian,这是由于这两个位置的hessian是转置的关系。而b则在行遍历的时候一行行填入。
void Problem::MakeHessian() {
TicToc t_h;
// 直接构造大的 H 矩阵
ulong size = ordering_generic_;
MatXX H(MatXX::Zero(size, size));
VecX b(VecX::Zero(size));
for (auto &edge: edges_) { // 遍历所有残差项,求解所有残差
edge.second->ComputeResidual();
edge.second->ComputeJacobians();
auto jacobians = edge.second->Jacobians(); // 取出
auto verticies = edge.second->Verticies();
assert(jacobians.size() == verticies.size());
for (size_t i = 0; i < verticies.size(); ++i) {
auto v_i = verticies[i];
if (v_i->IsFixed()) continue; // Hessian 里不需要添加它的信息,也就是它的雅克比为 0
auto jacobian_i = jacobians[i]; // 放入
ulong index_i = v_i->OrderingId();
ulong dim_i = v_i->LocalDimension(); // 告诉维度
MatXX JtW = jacobian_i.transpose() * edge.second->Information();
for (size_t j = i; j < verticies.size(); ++j) {
auto v_j = verticies[j];
if (v_j->IsFixed()) continue;
auto jacobian_j = jacobians[j];
ulong index_j = v_j->OrderingId();
ulong dim_j = v_j->LocalDimension();
assert(v_j->OrderingId() != -1);
MatXX hessian = JtW * jacobian_j;
// 所有的信息矩阵叠加起来
H.block(index_i,index_j, dim_i, dim_j).noalias() += hessian;
if (j != i) {
// 对称的下三角
H.block(index_j,index_i, dim_j, dim_i).noalias() += hessian.transpose();
}
}
b.segment(index_i, dim_i).noalias() -= JtW * edge.second->Residual();
}
}
Hessian_ = H;
b_ = b;
t_hessian_cost_ += t_h.toc();
// Eigen::JacobiSVD svd(H, Eigen::ComputeThinU | Eigen::ComputeThinV);
// std::cout << svd.singularValues() <
if (err_prior_.rows() > 0) {
b_prior_ -= H_prior_ * delta_x_.head(ordering_poses_); // update the error_prior
}
Hessian_.topLeftCorner(ordering_poses_, ordering_poses_) += H_prior_;
b_.head(ordering_poses_) += b_prior_;
delta_x_ = VecX::Zero(size); // initial delta_x = 0_n;
} 这 里 补 充 一 下 关 于 使 用 鲁 棒 核 函 数 修 改 残 差 和 信 息 矩 阵 的 代 码 解 析 \red{这里补充一下关于使用鲁棒核函数修改残差和信息矩阵的代码解析} 这里补充一下关于使用鲁棒核函数修改残差和信息矩阵的代码解析
【补充】鲁棒核函数的H矩阵以及b
鲁棒核函数会修改残差和信息矩阵,如果没有设置 robust cost function,就会返回原来的。
若使用鲁棒核函数,则下边的函数:
edge.second->Information()将变为:
edge.second->RobustInfo(drho,robustInfo);对于信息矩阵的修改实际就是在原先信息矩阵的基础上增加(乘以)权重信息。
void Edge::RobustInfo(double &drho, MatXX &info) const{
if(lossfunction_) // 核函数??
{
// double e2 = residual_.transpose() * information_ * residual_;
double e2 = this->Chi2(); // s (对应于上方的公式)
Eigen::Vector3d rho;
lossfunction_->Compute(e2,rho); // 计算鲁棒核函数以及相对于s的一、二阶导
VecX weight_err = sqrt_information_ * residual_;
// 对W矩阵的求解,完全对应公式17
MatXX robust_info(information_.rows(), information_.cols());
robust_info.setIdentity();
robust_info *= rho[1];
if(rho[1] + 2 * rho[2] * e2 > 0.)
{
robust_info += 2 * rho[2] * weight_err * weight_err.transpose(); // W权重因子
}
info = robust_info * information_; // 核函数的信息矩阵
drho = rho[1];
}
else
{
drho = 1.0;
info = information_;
}
}① lossfunction_->Compute(e2,rho);
这里只列举柯西鲁棒核函数的定义以及对s的一阶导的代码,完全对应上方公式,delta_ 指协方差矩阵的逆,也就是信息矩阵 ∑ − 1 \sum^{-1} ∑−1。:
void CauchyLoss::Compute(double err2, Eigen::Vector3d& rho) const {
double dsqr = delta_ * delta_; // c^2
double dsqrReci = 1. / dsqr; // 1/c^2
double aux = dsqrReci * err2 + 1.0; // 1 + e^2/c^2
rho[0] = dsqr * log(aux); // c^2 * log( 1 + e^2/c^2 )
rho[1] = 1. / aux; // rho'
rho[2] = -dsqrReci * std::pow(rho[1], 2); // rho''
}② 若使用鲁棒核函数则H矩阵和b向量都会相应改变,代码如下(完全对应上方知识点的公式):
MatXX JtW = jacobian_i.transpose() * robustInfo;
for (size_t j = i; j < verticies.size(); ++j)
{
auto v_j = verticies[j];
if (v_j->IsFixed()) continue;
auto jacobian_j = jacobians[j];
ulong index_j = v_j->OrderingId();
ulong dim_j = v_j->LocalDimension();
assert(v_j->OrderingId() != -1);
MatXX hessian = JtW * jacobian_j;
// 所有的信息矩阵叠加起来
H.block(index_i, index_j, dim_i, dim_j).noalias() += hessian;
if (j != i) {
// 对称的下三角
H.block(index_j, index_i, dim_j, dim_i).noalias() += hessian.transpose();
}
}
// 对应公式(17)等式的右侧
b.segment(index_i, dim_i).noalias() -= drho * jacobian_i.transpose()* edge.second->Information() * edge.second->Residual();注 意 关 于 H 先 验 信 息 的 处 理 , 留 有 后 用 \red{注意关于H先验信息的处理,留有后用} 注意关于H先验信息的处理,留有后用
主要操作为将相机帧和路标点的信息块设置为0。代码如下:
if(H_prior_.rows() > 0)
{
MatXX H_prior_tmp = H_prior_;
VecX b_prior_tmp = b_prior_;
/// 遍历所有 POSE 顶点,然后设置相应的先验维度为 0 . fix 外参数, SET PRIOR TO ZERO
/// landmark 没有先验
for (auto vertex: verticies_)
{
if (IsPoseVertex(vertex.second) && vertex.second->IsFixed() )
{
int idx = vertex.second->OrderingId();
int dim = vertex.second->LocalDimension();
//相机和路标点的信息删除
H_prior_tmp.block(idx,0, dim, H_prior_tmp.cols()).setZero();
H_prior_tmp.block(0,idx, H_prior_tmp.rows(), dim).setZero();
b_prior_tmp.segment(idx,dim).setZero();
}
}
Hessian_.topLeftCorner(ordering_poses_, ordering_poses_) += H_prior_tmp;
b_.head(ordering_poses_) += b_prior_tmp;
}2.3.3.3 LM算法的初始化
ComputeLambdaInitLM()函数用于计算阻尼因子的初始值
/// LM
void Problem::ComputeLambdaInitLM() {
ni_ = 2.;
currentLambda_ = -1.;
currentChi_ = 0.0;
// TODO:: robust cost chi2
for (auto edge: edges_) {
currentChi_ += edge.second->Chi2();
}
if (err_prior_.rows() > 0) // marg prior residual
currentChi_ += err_prior_.norm();
stopThresholdLM_ = 1e-6 * currentChi_; // 迭代条件为 误差下降 1e-6 倍
double maxDiagonal = 0;
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
for (ulong i = 0; i < size; ++i) {
maxDiagonal = std::max(fabs(Hessian_(i, i)), maxDiagonal); // fabs取绝对值
}
double tau = 1e-5;
currentLambda_ = tau * maxDiagonal;
}其中 τ \tau τ是一个系数,按工程经验取值(程序里取 1 0 − 5 10^{-5} 10−5)double tau = 1e-5;,最后阻尼因子的计算为currentLambda_ = tau * maxDiagonal;maxdiagonal是H矩阵对角线上最大的块。
【相关知识点】
double Edge::Chi2() {
// TODO:: we should not Multiply information here, because we have computed Jacobian = sqrt_info * Jacobian
return residual_.transpose() * information_ * residual_
// return residual_.transpose() * residual_; // 当计算 residual 的时候已经乘以了 sqrt_info, 这里不要再乘
}初始化完成之后就进入LM迭代求解的部分,迭代次数由solve函数的入口参数确定,非 SLAM 问题直接取逆求解( H不是稀疏的)。SLAM 问题采用舒尔补的计算方式求解 H δ x = b H\delta x = b Hδx=b。
2.3.3.4 LM算法基本流程
这一部分在前面2.3.3 solve函数部分的代码中已经展示,所以省略。
2.3.3.5 求解线性方程
SolveLinearSystem();
void Problem::SolveLinearSystem() {
if (problemType_ == ProblemType::GENERIC_PROBLEM) {
// 非 SLAM 问题直接求解
// PCG solver
MatXX H = Hessian_;
for (ulong i = 0; i < Hessian_.cols(); ++i) {
H(i, i) += currentLambda_; // H = J^t * J + Lambda * I
}
// delta_x_ = PCGSolver(H, b_, H.rows() * 2);
delta_x_ = Hessian_.inverse() * b_; // H不是稀疏的,直接取逆
} else {
// SLAM 问题采用舒尔补的计算方式
// step1: schur marginalization --> Hpp, bpp
int reserve_size = ordering_poses_;
int marg_size = ordering_landmarks_;
// TODO:: home work. 完成矩阵块取值,Hmm,Hpm,Hmp,bpp,bmm:landmark
MatXX Hmm = Hessian_.block(reserve_size,reserve_size, marg_size, marg_size);
MatXX Hmp = Hessian_.block(reserve_size,0, marg_size, reserve_size);
MatXX Hpm = Hessian_.block(0,reserve_size,reserve_size, marg_size);
VecX bmm = b_.segment(reserve_size,marg_size );
VecX bpp = b_.segment(0,reserve_size);
// Hmm 是对角线矩阵,它的求逆可以直接为对角线块分别求逆,如果是逆深度,对角线块为1维的,则直接为对角线的倒数,这里可以加速
MatXX Hmm_inv(MatXX::Zero(marg_size, marg_size));
for (auto landmarkVertex : idx_landmark_vertices_) {
int idx = landmarkVertex.second->OrderingId() - reserve_size; // landmark在后,pose在前
int size = landmarkVertex.second->LocalDimension();
Hmm_inv.block(idx, idx, size, size) = Hmm.block(idx, idx, size, size).inverse();
}
// TODO:: home work. 完成舒尔补 Hpp, bpp 代码
MatXX tempH = Hpm * Hmm_inv;
H_pp_schur_ = Hessian_.block(0,0,reserve_size,reserve_size) - tempH * Hmp;
b_pp_schur_ = bpp - tempH * bmm;
// step2: solve Hpp * delta_x = bpp
VecX delta_x_pp(VecX::Zero(reserve_size));
// PCG Solver
for (ulong i = 0; i < ordering_poses_; ++i) {
H_pp_schur_(i, i) += currentLambda_;
}
int n = H_pp_schur_.rows() * 2; // 迭代次数
delta_x_pp = PCGSolver(H_pp_schur_, b_pp_schur_, n); // 哈哈,小规模问题,搞 pcg 花里胡哨
delta_x_.head(reserve_size) = delta_x_pp; // xp:相机位姿放置在指定位置
// std::cout << delta_x_pp.transpose() << std::endl;
// TODO:: home work. step3: solve landmark
VecX delta_x_ll(marg_size);
delta_x_ll = Hmm_inv * (bmm - Hmp * delta_x_pp) ;
delta_x_.tail(marg_size) = delta_x_ll; // x_ll 路标点信息
}
}【相关知识点】
SLAM问题的求解
将问题转换成normal equation,其中, H p p H_{pp} Hpp表示相机位姿之间的关系,下图中 H l l H_{ll} Hll对应代码中的 H m m H_{mm} Hmm表示路标点之间的关系, H p l H_{pl} Hpl对应代码中的 H p m H_{pm} Hpm表示相机和路标之间的关系。
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第24张图片](http://img.e-com-net.com/image/info8/e319ea7196c840d2b34ad17ce328e4f2.jpg)
首先使用SolveLinearSystem();来求解 Δ x Δx Δx,如果求解后 Δ x Δx Δx的值够小则认为迭代成功,令stop = true;退出while循环,否则更新状态量并判断当前步是否可行,可行的话就在当前的状态量下求新的H和b,否则当发现误差没有下降的时候就进行回滚。同时如果当残差下降得够多也可以退出迭代(2.3.3 solve函数部分的代码中已经展示)。
2.3.3.6 更新状态量UpdateStates():
void Problem::UpdateStates()
{
// update vertex
for (auto vertex: verticies_)
{
// 备份参数
vertex.second->BackUpParameters(); // 保存上次的估计值
ulong idx = vertex.second->OrderingId();
ulong dim = vertex.second->LocalDimension();
VecX delta = delta_x_.segment(idx, dim); // H delta_x = b
vertex.second->Plus(delta); // +=
}
// update prior
if (err_prior_.rows() > 0)
{
// BACK UP b_prior_
b_prior_backup_ = b_prior_;
err_prior_backup_ = err_prior_;
/// update with first order Taylor, b' = b + \frac{\delta b}{\delta x} * \delta x
/// \delta x = Computes the linearized deviation from the references (linearization points)
b_prior_ -= H_prior_ * delta_x_.head(ordering_poses_); // update the error_prior
err_prior_ = -Jt_prior_inv_ * b_prior_.head(ordering_poses_ - 15);
}
}
2.3.3.7 判断当前步是否可行以及 LM 的 lambda 怎么更新
Problem::IsGoodStepInLM()此函数的详细代码解析以及知识点可见我的另一篇博客——阻尼因子更新策略(Nielsen)
2.3.3.8 回滚操作
void Problem::RollbackStates()
{
// update vertex
for (auto vertex: verticies_)
{
vertex.second->RollBackParameters();
}
// Roll back prior_
if (err_prior_.rows() > 0)
{
b_prior_ = b_prior_backup_;
err_prior_ = err_prior_backup_;
}
} void RollBackParameters() { parameters_ = parameters_backup_; }求解完problem整个问题BA就结束了!
3. 边缘化的测试函数
其例子为:
设 x 2 x_2 x2为室外的温度 x 1 , x 3 x_1, x_3 x1,x3分别为房间1和房间 3的室内温度,三个变量有以下关系: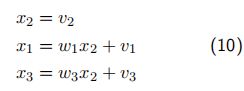
图例为:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第25张图片](http://img.e-com-net.com/image/info8/e042204efdac4932b017d747da67d2f4.jpg)
其中, v i v_i vi相互独立,且各自服从协方差为 σ i 2 σ^2_i σi2 的高斯分布。
则其信息矩阵求解为:
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第26张图片](http://img.e-com-net.com/image/info8/fe4907f1f0d146e8ae01b5ff699b5992.jpg)
现在要从这个例子中marg掉 x 2 x_2 x2(绿色部分),求解之后的信息矩阵。需要将绿色部分移动到信息矩阵的右下角,具体操作为先二、三行互换,再二、三列互换。然后进行舒尔补运算,marg掉 x 2 x_2 x2。程序如下:
void Problem::TestMarginalize() { // marg第二个变量
// Add marg test
int idx = 1; // marg 中间那个变量
int dim = 1; // marg 变量的维度
int reserve_size = 3; // 总共变量的维度
double delta1 = 0.1 * 0.1;
double delta2 = 0.2 * 0.2;
double delta3 = 0.3 * 0.3;
int cols = 3;
MatXX H_marg(MatXX::Zero(cols, cols));
H_marg << 1./delta1, -1./delta1, 0,
-1./delta1, 1./delta1 + 1./delta2 + 1./delta3, -1./delta3,
0., -1./delta3, 1/delta3;
std::cout << "---------- TEST Marg: before marg------------"<< std::endl;
std::cout << H_marg << std::endl;
// TODO:: home work. 将变量移动到右下角
/// 准备工作: move the marg pose to the Hmm bottown right
// 将 row i 移动矩阵最下面
Eigen::MatrixXd temp_rows = H_marg.block(idx, 0, dim, reserve_size); //第二行
Eigen::MatrixXd temp_botRows = H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size); // 第三行
H_marg.block(idx, 0,reserve_size - idx - dim, reserve_size) = temp_botRows; // 二、三行颠倒
H_marg.block(reserve_size - dim, 0, dim, reserve_size) = temp_rows;
// 将 col i 移动矩阵最右边
Eigen::MatrixXd temp_cols = H_marg.block(0, idx, reserve_size, dim); // 第二列
Eigen::MatrixXd temp_rightCols = H_marg.block(0, idx + dim, reserve_size, reserve_size - idx - dim); // 第三列
H_marg.block(0, idx, reserve_size, reserve_size - idx - dim) = temp_rightCols; // 二、三列颠倒
H_marg.block(0, reserve_size - dim, reserve_size, dim) = temp_cols;
std::cout << "---------- TEST Marg: 将变量移动到右下角------------"<< std::endl;
std::cout<< H_marg <<std::endl;
/// 开始 marg : schur
double eps = 1e-8;
int m2 = dim;
int n2 = reserve_size - dim; // 剩余变量的维度
Eigen::MatrixXd Amm = 0.5 * (H_marg.block(n2, n2, m2, m2) +
H_marg.block(n2, n2, m2, m2).transpose());
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd(
(saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() *
saes.eigenvectors().transpose();
// TODO:: home work. 完成舒尔补操作
Eigen::MatrixXd Arm = H_marg.block(0,n2,n2,m2);
Eigen::MatrixXd Amr = H_marg.block(n2,0,m2,n2);
Eigen::MatrixXd Arr = H_marg.block(0,0,n2,n2);
Eigen::MatrixXd tempB = Arm * Amm_inv;
Eigen::MatrixXd H_prior = Arr - tempB * Amr;
std::cout << "---------- TEST Marg: after marg------------"<< std::endl;
std::cout << H_prior << std::endl;
}![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第1张图片](http://img.e-com-net.com/image/info8/afb87128f88f4b0fbe43dd03175ebaa1.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第2张图片](http://img.e-com-net.com/image/info8/5383ef023d1d4919824fee9c447eda5e.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第3张图片](http://img.e-com-net.com/image/info8/8a0834d6b9094fc589625b408d21e1e3.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第4张图片](http://img.e-com-net.com/image/info8/f114f3a3381c4086afd1f2dae55c79d3.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第5张图片](http://img.e-com-net.com/image/info8/4adfe62c2d6741fe8a0d60a598ced1e2.png)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第7张图片](http://img.e-com-net.com/image/info8/2b4d74f9435d4e7f9dfa4c0ef166639d.png)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第10张图片](http://img.e-com-net.com/image/info8/32646241260643b9856750a6b906ba87.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第17张图片](http://img.e-com-net.com/image/info8/16805081bade42649a14b0c24b8e82d2.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第20张图片](http://img.e-com-net.com/image/info8/dff360ccbcbe49f69b3d826a1f6b80c7.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第21张图片](http://img.e-com-net.com/image/info8/93ef0dc014e34a23ba582dbe3e6f9a8e.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第22张图片](http://img.e-com-net.com/image/info8/793004a3514049fa8a40a96d8431f2d7.jpg)
![[从零手写VIO|第五节]——后端优化实践——单目BA求解代码解析_第23张图片](http://img.e-com-net.com/image/info8/e9ef699ba17649d2a47825e07221fa83.jpg)