强化学习课程学习（6）——基于深度学习方法求解RL

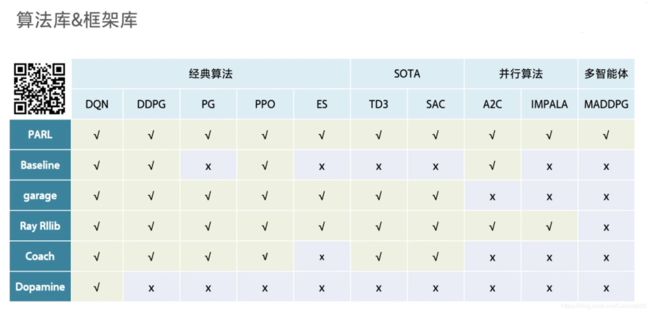
在之前讲到了强化学习求解方法，无论是动态规划DP，蒙特卡罗方法MC，还是时序差分TD，使用的状态都是离散的有限个状态集合$S$。此时问题的规模比较小，比较容易求解。但是假如我们遇到复杂的状态集合呢？甚至很多时候，状态是连续的，那么就算离散化后，集合也很大，此时我们的传统方法，比如Q-Learning，根本无法在内存中维护这么大的一张Q表。对此，随着深度学习地方法的发展兴起，基于深度学习的算法模型开始流行起来——Deep Q-learning、Nature DQN、Double DQN、Prioritized Replay DQN、Dueling DQN等算法模型。可见下表所有的算法框架：

DQN

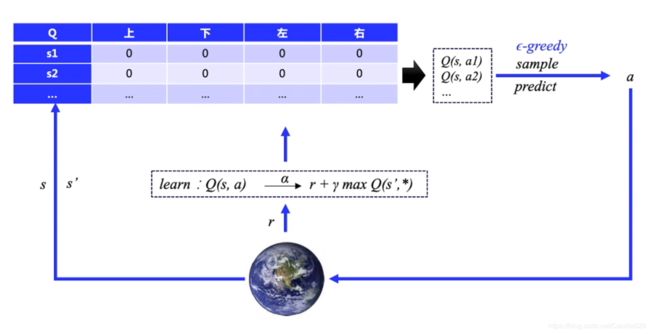
Deep Q-Learning算法的基本思路来源于Q-Learning（基于Q表格）。但是和Q-Learning不同的地方在于，它的Q值的计算不是直接通过状态值$s$和动作来计算，而是通过上面讲到的Q网络来计算的。这个Q网络是一个神经网络，我们一般简称Deep Q-Learning为DQN。

---

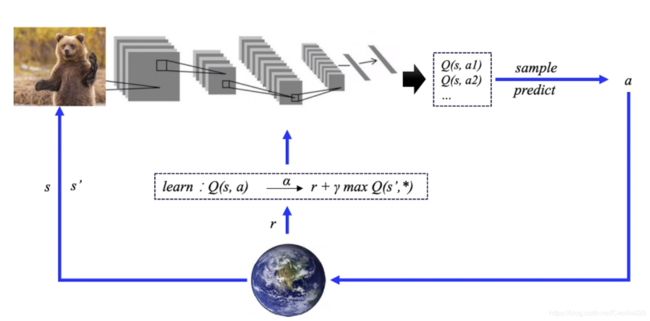
从Q表格变成了神经网络结构!!!

​ DQN的输入是我们的状态$s$对应的状态向量$\varphi (s)$， 输出是所有动作在该状态下的动作价值函数Q。Q网络可以是DNN，CNN或者RNN，没有具体的网络结构要求。

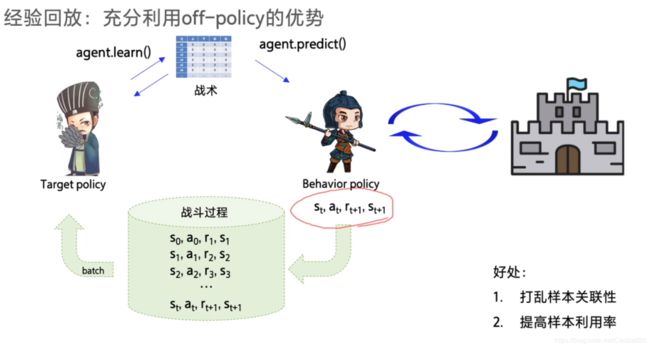
​ DQN主要使用的技巧是经验回放（experience replay）,即将每次和环境交互得到的奖励与状态更新情况都保存起来，用于后面目标Q值的更新。为什么需要经验回放呢？我们回忆一下Q-Learning，它是有一张Q表来保存所有的Q值的当前结果的，但是DQN是没有的，那么在做动作价值函数更新的时候，就需要其他的方法，这个方法就是经验回放。

通过经验回放得到的目标Q值和通过Q网络计算的Q值肯定是有误差的，那么我们可以通过梯度的反向传播来更新神经网络的参数$w$，当$w$收敛后，我们的就得到的近似的Q值计算方法，进而贪婪策略也就求出来了。

相比Q-learning总结DQN的创新之处：

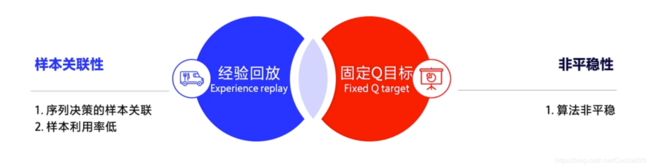
在Q-learning的基础上，DQN提出了两个技巧使得Q网络的更新迭代更稳定。

• 经验回放 Experience Replay：主要解决样本关联性和利用效率的问题。使用一个经验池存储多条经验s,a,r,s'，再从中随机抽取一批数据送去训练。

• 固定Q目标 Fixed-Q-Target：主要解决算法训练不稳定的问题。复制一个和原来Q网络结构一样的Target Q网络，用于计算Q目标值。

  

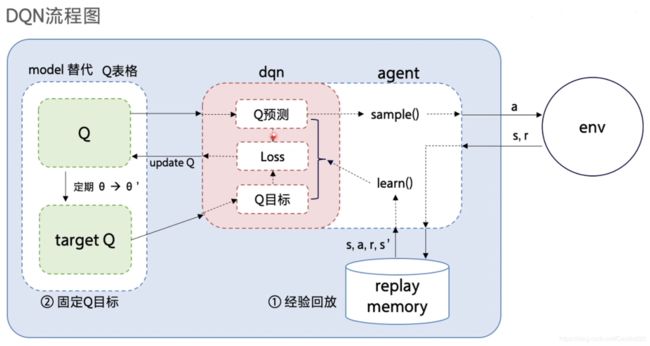
DQN算法流程图

实例——小车CartPole问题

使用DQN解决CartPole问题，移动小车使得车上的摆杆倒立起来。
导入依赖后，搭建Model、Algorithm、Agent架构

• Agent把产生的数据传给algorithm，algorithm根据model的模型结构计算出- Loss，使用SGD或者其他优化器不断的优化，PARL这种架构可以很方便的应用在各类深度强化学习问题中(百度封装并构建好了的框架)。
• Model用来定义前向(Forward)网络，用户可以自由的定制自己的网络结构。
• Algorithm 定义了具体的算法来更新前向网络(Model)，也就是通过定义损失函数来更新Model，和算法相关的计算都放在algorithm中。

# from parl.algorithms import DQN # 也可以直接从parl库中导入DQN算法

class DQN(parl.Algorithm):
    def __init__(self, model, act_dim=None, gamma=None, lr=None):
        """ DQN algorithm
        
        Args:
            model (parl.Model): 定义Q函数的前向网络结构
            act_dim (int): action空间的维度，即有几个action
            gamma (float): reward的衰减因子
            lr (float): learning rate 学习率.
        """
        self.model = model
        self.target_model = copy.deepcopy(model)

        assert isinstance(act_dim, int)
        assert isinstance(gamma, float)
        assert isinstance(lr, float)
        self.act_dim = act_dim
        self.gamma = gamma
        self.lr = lr

    def predict(self, obs):
        """ 使用self.model的value网络来获取 [Q(s,a1),Q(s,a2),...]
        """
        return self.model.value(obs)

    def learn(self, obs, action, reward, next_obs, terminal):
        """ 使用DQN算法更新self.model的value网络
        """
        # 从target_model中获取 max Q' 的值，用于计算target_Q
        next_pred_value = self.target_model.value(next_obs)
        best_v = layers.reduce_max(next_pred_value, dim=1)
        best_v.stop_gradient = True  # 阻止梯度传递
        terminal = layers.cast(terminal, dtype='float32')
        target = reward + (1.0 - terminal) * self.gamma * best_v

        pred_value = self.model.value(obs)  # 获取Q预测值
        # 将action转onehot向量，比如：3 => [0,0,0,1,0]
        action_onehot = layers.one_hot(action, self.act_dim)
        action_onehot = layers.cast(action_onehot, dtype='float32')
        # 下面一行是逐元素相乘，拿到action对应的 Q(s,a)
        # 比如：pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]]
        #  ==> pred_action_value = [[3.9]]
        pred_action_value = layers.reduce_sum(
            layers.elementwise_mul(action_onehot, pred_value), dim=1)

        # 计算 Q(s,a) 与 target_Q的均方差，得到loss
        cost = layers.square_error_cost(pred_action_value, target)
        cost = layers.reduce_mean(cost)
        optimizer = fluid.optimizer.Adam(learning_rate=self.lr)  # 使用Adam优化器
        optimizer.minimize(cost)
        return cost

    def sync_target(self):
        """ 把 self.model 的模型参数值同步到 self.target_model
        """
        self.model.sync_weights_to(self.target_model)

构建Agent

class Agent(parl.Agent):
    def __init__(self,
                 algorithm,
                 obs_dim,
                 act_dim,
                 e_greed=0.1,
                 e_greed_decrement=0):
        assert isinstance(obs_dim, int)
        assert isinstance(act_dim, int)
        self.obs_dim = obs_dim
        self.act_dim = act_dim
        super(Agent, self).__init__(algorithm)

        self.global_step = 0
        self.update_target_steps = 200  # 每隔200个training steps再把model的参数复制到target_model中

        self.e_greed = e_greed  # 有一定概率随机选取动作，探索
        self.e_greed_decrement = e_greed_decrement  # 随着训练逐步收敛，探索的程度慢慢降低

    def build_program(self):
        self.pred_program = fluid.Program()
        self.learn_program = fluid.Program()

        with fluid.program_guard(self.pred_program):  # 搭建计算图用于 预测动作，定义输入输出变量
            obs = layers.data(
                name='obs', shape=[self.obs_dim], dtype='float32')
            self.value = self.alg.predict(obs)

        with fluid.program_guard(self.learn_program):  # 搭建计算图用于 更新Q网络，定义输入输出变量
            obs = layers.data(
                name='obs', shape=[self.obs_dim], dtype='float32')
            action = layers.data(name='act', shape=[1], dtype='int32')
            reward = layers.data(name='reward', shape=[], dtype='float32')
            next_obs = layers.data(
                name='next_obs', shape=[self.obs_dim], dtype='float32')
            terminal = layers.data(name='terminal', shape=[], dtype='bool')
            self.cost = self.alg.learn(obs, action, reward, next_obs, terminal)

    def sample(self, obs):
        sample = np.random.rand()  # 产生0~1之间的小数
        if sample < self.e_greed:
            act = np.random.randint(self.act_dim)  # 探索：每个动作都有概率被选择
        else:
            act = self.predict(obs)  # 选择最优动作
        self.e_greed = max(
            0.01, self.e_greed - self.e_greed_decrement)  # 随着训练逐步收敛，探索的程度慢慢降低
        return act

    def predict(self, obs):  # 选择最优动作
        obs = np.expand_dims(obs, axis=0)
        pred_Q = self.fluid_executor.run(
            self.pred_program,
            feed={'obs': obs.astype('float32')},
            fetch_list=[self.value])[0]
        pred_Q = np.squeeze(pred_Q, axis=0)
        act = np.argmax(pred_Q)  # 选择Q最大的下标，即对应的动作
        return act

    def learn(self, obs, act, reward, next_obs, terminal):
        # 每隔200个training steps同步一次model和target_model的参数
        if self.global_step % self.update_target_steps == 0:
            self.alg.sync_target()
        self.global_step += 1

        act = np.expand_dims(act, -1)
        feed = {
            'obs': obs.astype('float32'),
            'act': act.astype('int32'),
            'reward': reward,
            'next_obs': next_obs.astype('float32'),
            'terminal': terminal
        }
        cost = self.fluid_executor.run(
            self.learn_program, feed=feed, fetch_list=[self.cost])[0]  # 训练一次网络
        return cost

创建经验池ReplayMemory用于经验回收

import random
import collections
import numpy as np


class ReplayMemory(object):
    def __init__(self, max_size):
        self.buffer = collections.deque(maxlen=max_size)

    # 增加一条经验到经验池中
    def append(self, exp):
        self.buffer.append(exp)

    # 从经验池中选取N条经验出来
    def sample(self, batch_size):
        mini_batch = random.sample(self.buffer, batch_size)
        obs_batch, action_batch, reward_batch, next_obs_batch, done_batch = [], [], [], [], []

        for experience in mini_batch:
            s, a, r, s_p, done = experience
            obs_batch.append(s)
            action_batch.append(a)
            reward_batch.append(r)
            next_obs_batch.append(s_p)
            done_batch.append(done)

        return np.array(obs_batch).astype('float32'), \
            np.array(action_batch).astype('float32'), np.array(reward_batch).astype('float32'),\
            np.array(next_obs_batch).astype('float32'), np.array(done_batch).astype('float32')

    def __len__(self):
        return len(self.buffer)

Nature DQN

DQN中目标Q值的计算使用到了当前要训练的Q网络参数来计算$Q(\varphi (S\prime j),A\prime j,w)$，而实际上，我们又希望通过$y_i$来后续更新Q网络参数。这样两者循环依赖，迭代起来两者的相关性过强,不利于算法的收敛。

对此，Nature DQN使用了两个Q网络，一个当前Q网络QQ用来选择动作，更新模型参数，另一个目标Q网络Q′用于计算目标Q值。目标Q网络的网络参数不需要迭代更新，而是每隔一段时间从当前Q网络Q复制过来，即延时更新，这样可以减少目标Q值和当前的Q值相关性。

注意的是，两个Q网络的结构是一模一样，除了用一个新的相同结构的目标Q网络来计算目标Q值以外，其余部分基本是完全相同的，这样才可以复制网络参数。

Double DQN

Nature DQN的算法流程，它通过使用两个相同的神经网络，以解决数据样本和网络训练之前的相关性。所有的目标Q值都是通过贪婪法直接得到的，无论是Q-Learning，DQN还是 Nature DQN，都是如此。比如对于Nature DQN,虽然用了两个Q网络并使用目标Q网络计算Q值，其第j个样本的目标Q值的计算还是贪婪法得到的，计算入下式：
$$y_j=\{\begin{array}{ll}{R}_j& is\_en{d}_{j}istrue\\ R_j+\gamma {\max }_{a^{\prime }}{Q}^{\prime }(\varphi (S_j^{\prime }),A_j^{\prime },w^{\prime })& is\_en{d}_{j}isfalse\end{array}$$
使用max虽然可以快速让Q值向可能的优化目标靠拢，但是很容易过犹不及，导致过度估计(Over Estimation)，所谓过度估计就是最终我们得到的算法模型有很大的偏差(bias)。为了解决这个问题， DDQN通过解耦目标Q值动作的选择和目标Q值的计算这两步，来达到消除过度估计的问题。

Prioritized Replay DQN

DDQN使用两个Q网络，用当前Q网络计算最大Q值对应的动作，用目标Q网络计算这个最大动作对应的目标Q值，进而消除贪婪法带来的偏差。

Prioritized Replay DQN在DDQN的基础上，对经验回放部分的逻辑做优化。在经验回放池里面的不同的样本由于TD误差的不同，对我们反向传播的作用是不一样的。TD误差越大，那么对我们反向传播的作用越大。而TD误差小的样本，由于TD误差小，对反向梯度的计算影响不大。在Q网络中，TD误差就是目标Q网络计算的目标Q值和当前Q网络计算的Q值之间的差距。这样如果TD误差的绝对值$|\delta (t)|$较大的样本更容易被采样，则我们的算法会比较容易收敛。Prioritized Replay DQN根据每个样本的TD误差绝对值$|\delta (t)|$，给定该样本的优先级正比于$|\delta (t)|$，将这个优先级的值存入经验回放池。

Dueling DQN

在前面讲到的DDQN中，我们通过优化目标Q值的计算来优化算法，在Prioritized Replay DQN中，我们通过优化经验回放池按权重采样来优化算法。而在Dueling DQN中，我们尝试通过优化神经网络的结构来优化算法。

​ 具体如何优化网络结构呢？Dueling DQN考虑将Q网络分成两部分，第一部分是仅仅与状态$S$有关，与具体要采用的动作$A$无关，这部分我们叫做价值函数部分，记做V(S,w,α),第二部分同时与状态状态$S$和动作$A$有关，这部分叫做优势函数(Advantage Function)部分,记为$A(S,A,w,\beta )$,那么最终我们的价值函数可以重新表示为：
$$\begin{gathered} Q(S,A,w,\alpha ,\beta )=V(S,w,\alpha )+A(S,A,w,\beta ) \\ 其中，w是公共部分的网络参数，而\alpha 是价值函数独有部分 \\ 的网络参数，而\beta 是优势函数独有部分的网络参数。 \end{gathered}$$

1.DQN家族的算法远远不止这些，还有一些其他的DQN算法我没有详细介绍，比如使用一些较复杂的CNN和RNN网络来提高DQN的表达能力，又比如改进探索状态空间的方法等，主要是在DQN的基础上持续优化。
2.DQN算是深度强化学习的中的主流流派，代表了Value-Based这一大类深度强化学习算法。但是它也有自己的一些问题，就是绝大多数DQN只能处理离散的动作集合，不能处理连续的动作集合。虽然NAF DQN可以解决这个问题，但是方法过于复杂了。而深度强化学习的另一个主流流派Policy-Based而可以较好的解决这个问题.。

以上所有版本的代码都是基于百度开发的paddlepaddle和parl框架实现的，版本是paddlepaddle=1.6.3和parl=1.3.1!

感谢百度AI studio提供学习资料和平台，感谢科科老师的讲解！