对二分查找法的理解。
以下任何言论都完全是个人的理解,如有雷同纯属巧合,如有错误,希望大家多多指出,共同学习!谢谢!
二分查找法,是一个比较高效的查找数组中某一个元素对应的索引的算法。
使用二分查找法的前提是目标数组必须是有序的,且没有重复元素的数组。
先思考一个问题,给你一个有序没有重复的int数组。让你找出某一个元素对应的索引。你会怎么做呢?
对于刚学习JAVA的朋友,可能脑子中第一想法就是循环遍历。
代码如下:
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
写完这个代码后我们来思考一下。
如果按照上面的代码进行查找的话,是能够实现的。不过程序员的差别就在于在实现功能的前提下,代码的效率才能决定你是否是一个优质的程序员。
上面的代码在每一次查找的时候,都要循环遍历这个数组。如果目标元素在数组的前端还好。如果目标元素是最后一个元素,或者这个数组有很庞大的元素量,那么这个代码其实是特别耗时,效率特别低的。
因此二分查找的算法就是用来解决这个问题的!
二分查找分析:
再重复一下。二分查找法的前提是目标数组必须是有序的,且没有重复元素的数组。
假如我有一个数组是
int[] array = {3, 5, 7, 8, 10, 15, 18, 20, 26, 30};
这个数组是有序且没有重复的。
假如我们要查找20这个元素的索引
如果按照刚才方法,我们循环遍历这个array,只有循环到第8次的时候才能找到20这个元素,才能查找到20对应的索引是7,然后跳出循环。
如果使用二分查找的话,
我们知道array 这个数组第一个索引是0,也知道最后一个元素的索引是array.length - 1。
int startIndex = 0;
int endIndex = array.length - 1;
那么我们计算出来中间的索引值,就是
int middleIndex = (startIndex + endIndex) / 2;
也就是5.
那么我们就通过中间这个索引把中间这个元素取出来,和20这个目标元素进行对比。
中间的元素是15.
20 大于 15,又因为这个array是有序的,那么15这个元素左边的(包括15)都可以排除掉了,
(如果我们查找的是其它元素,比15小,那么我们就把15右边所有的元素给排除掉了,那么endIndex = middleIndex - 1)
那么我们查找的目标就锁定在剩下的18 20 26 30上面了。
因为刚才我们的startIndex 指向了0,但15之前的已经被排除了。
所以我们的startIndex现在就变成了middleIndex + 1。
那么我们再次取middleIndex = (startIndex + endIndex) / 2;
这次得到的是7. -------------> (6 + 9) / 2 转成int型为7
那么我们通过7这个Index 再进行二分查找。
查找到7这个索引上的元素正好就是20.
所以使用二分查找只用进行两2查找即可找到20这个元素对应的索引。
而我们一个一个遍历这个数组的话,我们需要查找7次!
因此减少了5次没有必要的查询。
可能有些朋友觉得没有减少几次,但如果你查找的这个数组有10万,100万个元素,那么二分查找法是不是一个很高效的算法呢?
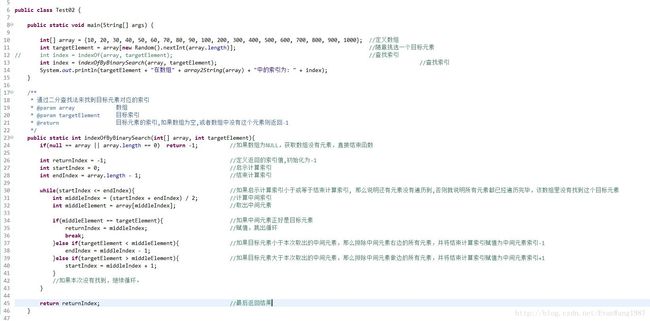
下面贴一下示例代码:
OK,到此二分查找复习完毕。最后附上代码。
点击下载源码