leetcode-二分查找总结(34,240,1111,162,658;153,154,33,81;287,875,1011,1283;528,497,1292)
一:经典的类似二分题目:
1:34:https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/
题目:
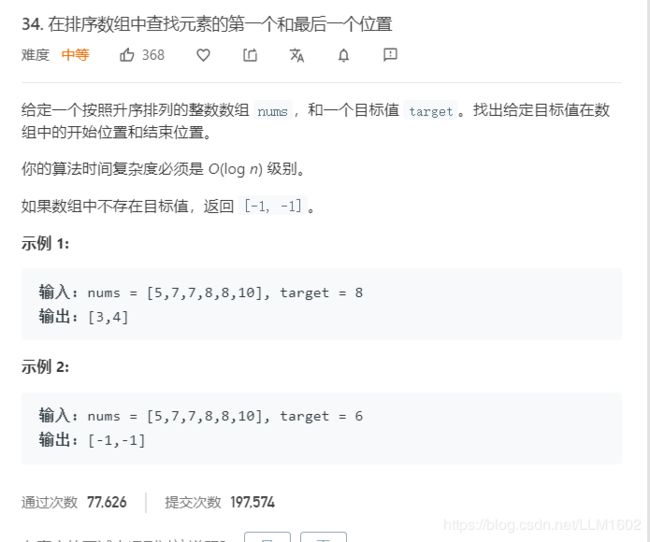
思路:直接二分,但是要分开找,先找左边界,利用第一次的找到的l,结合r = len,一起再找右边界
代码:
2:240:https://leetcode-cn.com/problems/search-a-2d-matrix-ii/
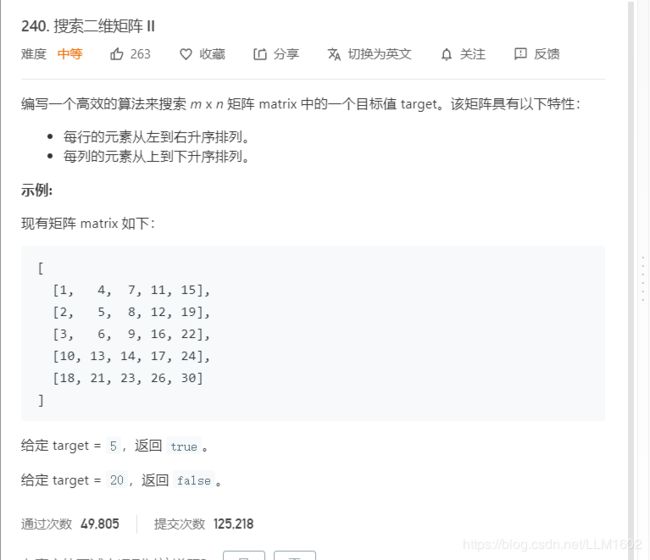
题目:
思路:总左下角开始比较,比target小,则列++,否则行--;
3:1111:https://leetcode-cn.com/problems/maximum-nesting-depth-of-two-valid-parentheses-strings/
题目:这题用贪心反而好理解些
思路:// 如果目前是左括号则数量加 1, 之后若现在有奇数个左括号则给 0, 偶数个左括号给 1
// 如果目前是右括号, 则抵消掉一个左括号, 若剩余奇数个左括号则给 1, 偶数个则给 0 (和上一行描述相反)
代码:
4:162:https://leetcode-cn.com/problems/find-peak-element/
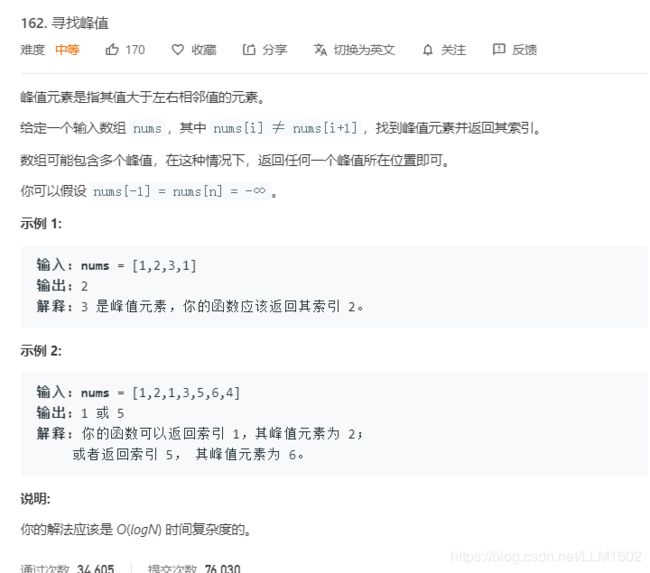
题目:
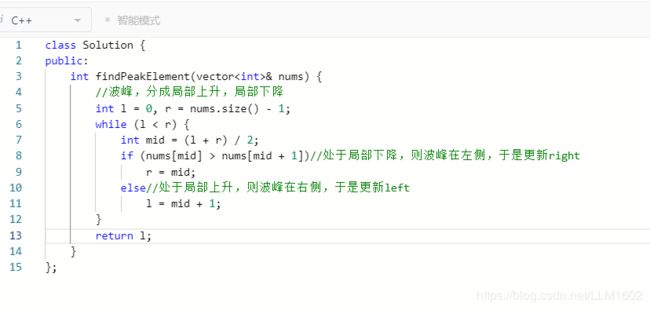
思路:通过比较mid,和mid+1代表的值,从而确定是局部上升还是局部下降,处于局部下降,则波峰在左侧,否则在右侧
代码:
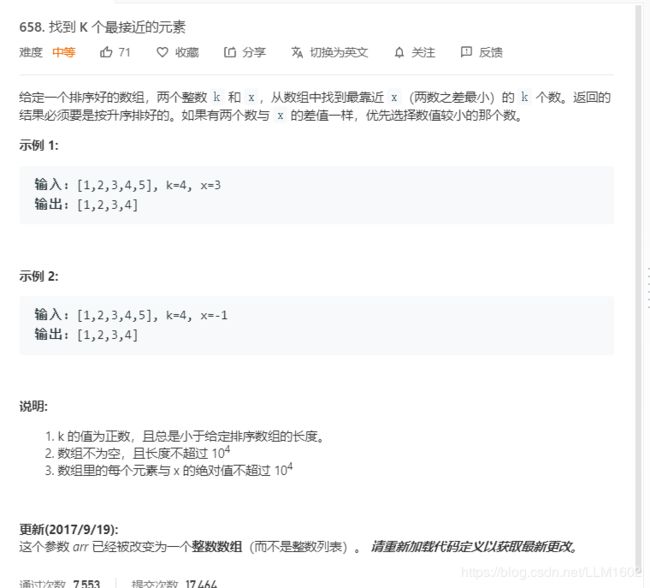
5:658:https://leetcode-cn.com/problems/find-k-closest-elements/
题目:
思路: // 假设 mid 是左边界,则当前区间覆盖的范围是 [mid, mid + k -1].
//如果发现 a[mid] 与 x 距离比 a[mid + k] 与 x 的距离要大,说明解一定在右侧。
代码:
二:旋转数组中用二分查找(二分变型)
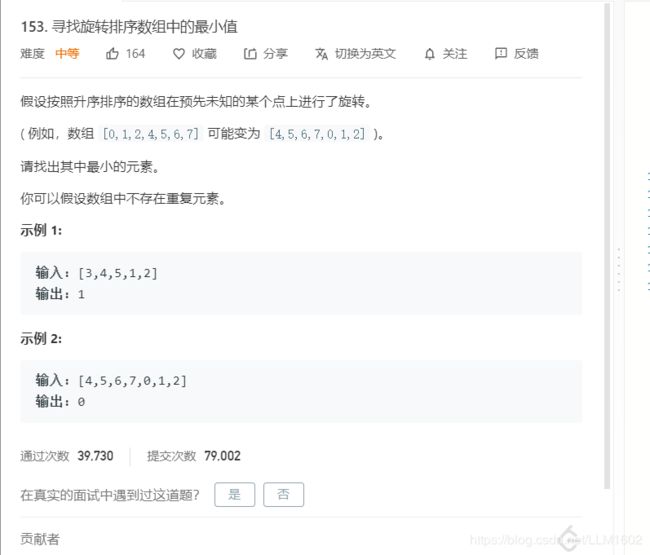
1:153:https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/
题目:
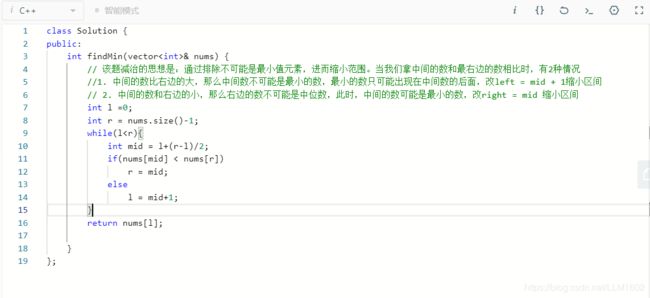
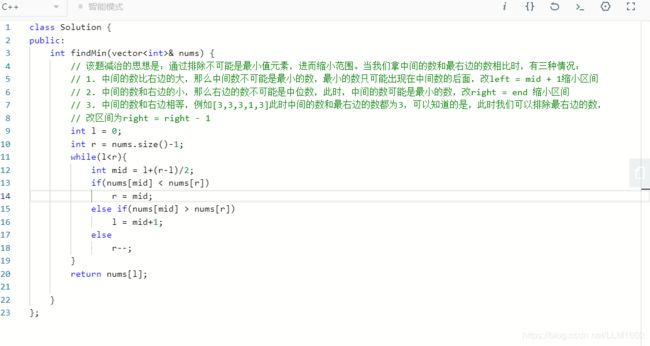
思路:通过排除最小元素不可能在哪里,从而缩小区间,当我们拿中间的数和最右边的数相比时,有2种情况
//1. 中间的数比右边的大,那么中间数不可能是最小的数,最小的数只可能出现在中间数的后面,改left = mid + 1缩小区间
// 2. 中间的数和右边的小,那么右边的数不可能是中位数,此时,中间的数可能是最小的数,改right = mid 缩小区间
代码:
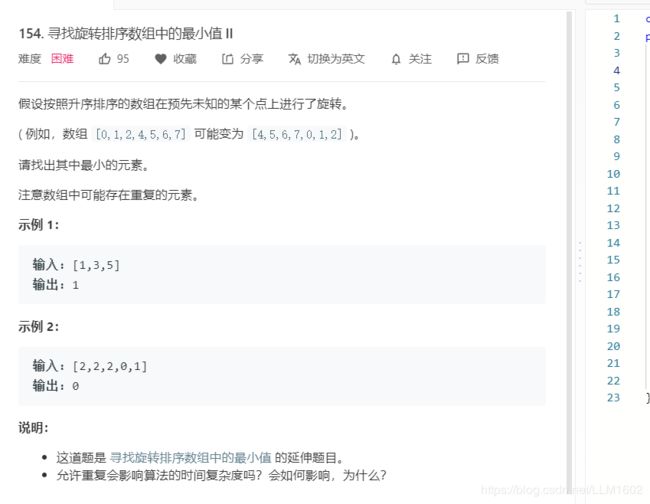
154:https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/
题目:
思路:基本同上一题,只是因为有重复元素的出现,多了情况3
// 3. 中间的数和右边相等,例如[3,3,3,1,3]此时中间的数和最右边的数都为3,可以知道的是,此时我们可以排除最右边的数,改区间为right = right - 1
代码:
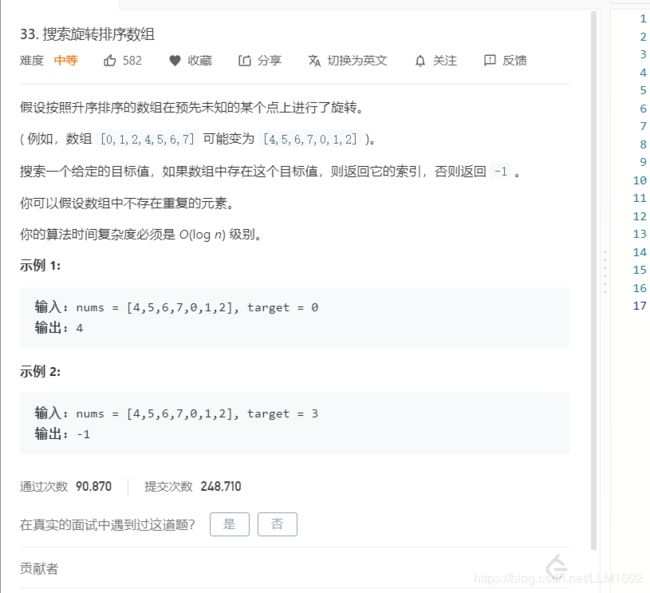
3:33:https://leetcode-cn.com/problems/search-in-rotated-sorted-array/
思路:这题比前两题稍微麻烦一些,因为还要同时比较target,但是基本思想差不多,先确定哪边区间是有序的,然后再确定与target的大小关系。
代码:
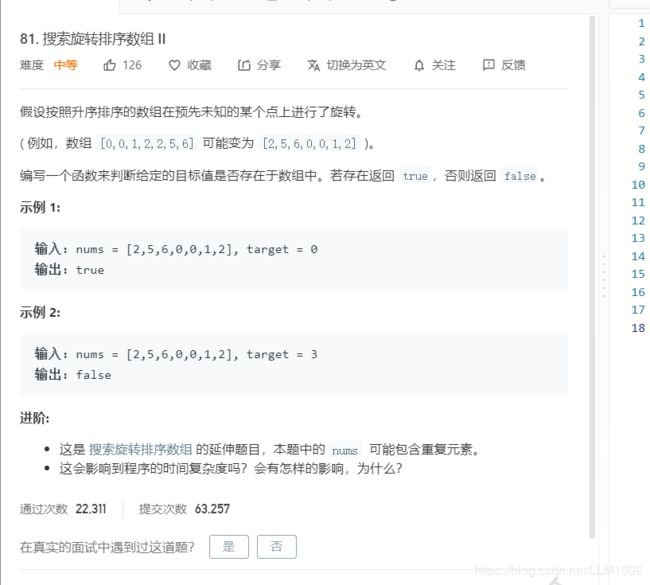
81:https://leetcode-cn.com/problems/search-in-rotated-sorted-array-ii/
题目:
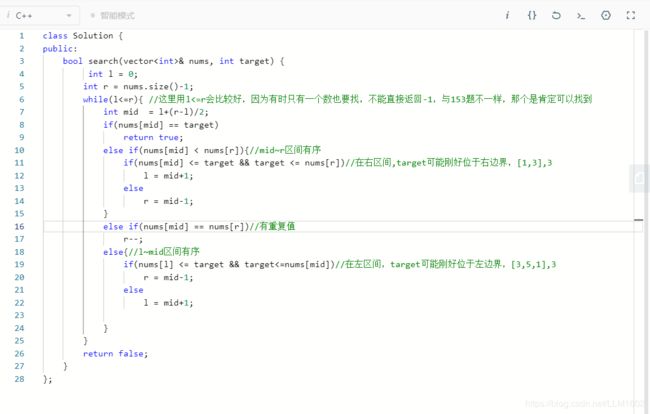
思路:同33,这里多了一些重复元素,需要在判断时对重复的处理以下;
代码:
三:二分+符合一定条件得遍历(看题目吧)
1:287 :https://leetcode-cn.com/problems/find-the-duplicate-number/
题目:
思路:由于题目很多限制,因此选用二分比较合适,但是怎么才能利用二分呢?一开始不知道怎么下手,仔细审题,从该数组的数都 是1~N入手,
// 以 [1, 2, 2, 3, 4, 5, 6, 7] 为例,一共 8 个数,n + 1 = 8,n = 7,根据题目意思,每个数都在 1 和 7 之间。
// 例如:区间 [1, 7] 的中位数是 4,遍历整个数组,统计小于等于 4 的整数的个数,至多应该为 4 个。换句话说,
// 整个数组里小于等于 4 的整数的个数如果严格大于 4 个,就说明重复的数存在于区间 [1, 4],
// 它的反面是:重复的数存在于区间 [5, 7]。
// 于是,二分法的思路是先猜一个数(有效范围 [left, right]里的中间数 mid),
代码:
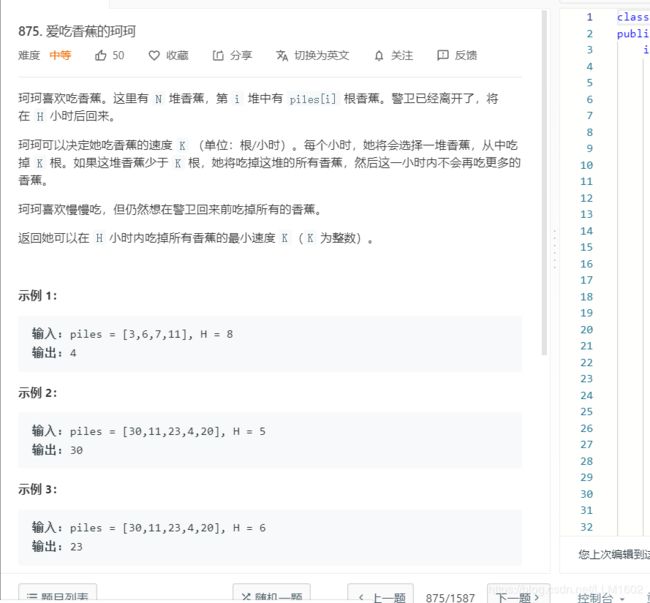
2:875: https://leetcode-cn.com/problems/koko-eating-bananas/
题目:
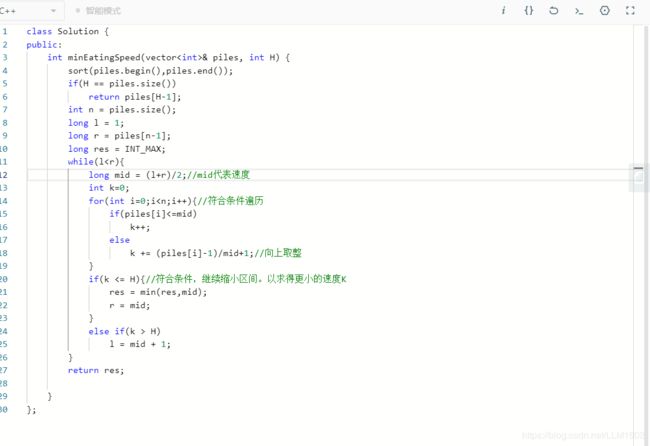
思路:基本是二分的思路,相当于你直接设一个速度k,然后计算以速度K来吃香蕉,需要多少个小时,如果时间长于所规定的,那么肯定是速度慢了,也就是k要变大,则令l = mid+1,否则说明这个速度是符合要求的,题目要求符合要求的最小速度,因此,可继续缩小区间,令r = mid,同时记录当前的速度
代码:
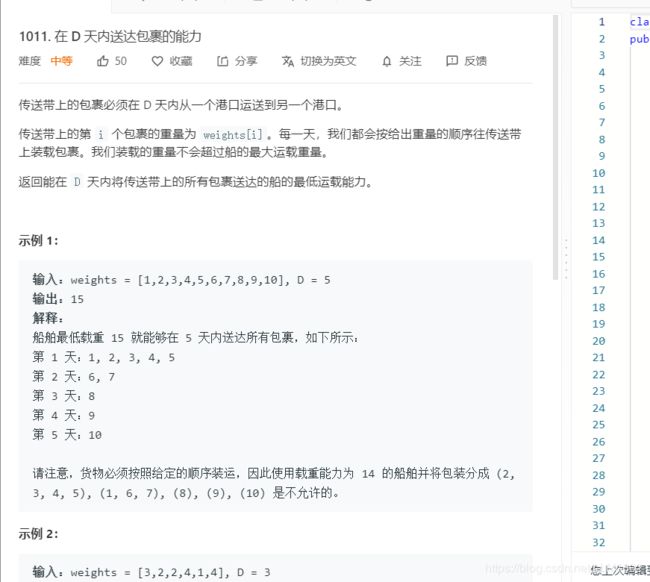
3:1011 : https://leetcode-cn.com/problems/capacity-to-ship-packages-within-d-days/
题目:
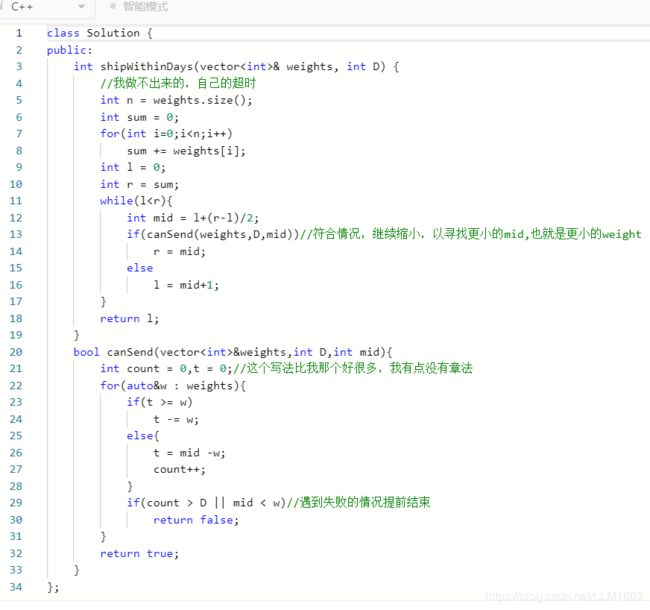
思路:基本思路同上,只不过这个for循环遍历的时候,计算需要多少天有点技巧,
代码:
4:1283:https://leetcode-cn.com/problems/find-the-smallest-divisor-given-a-threshold/
题目:
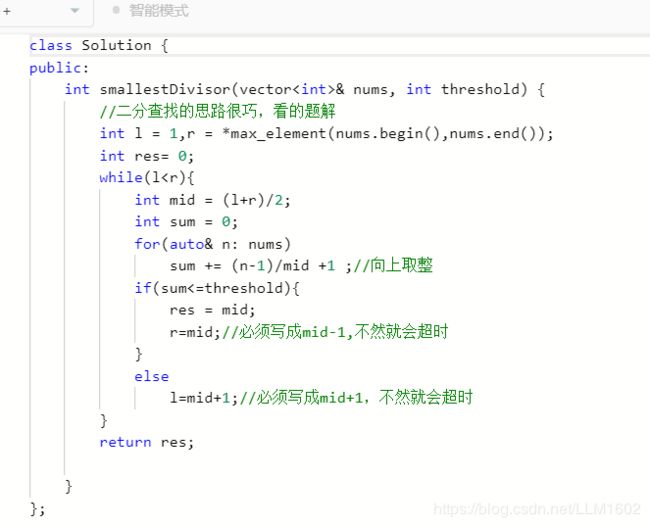
思路:依旧一样的思路,算出mid 然后计数
代码:
总结:
代码:
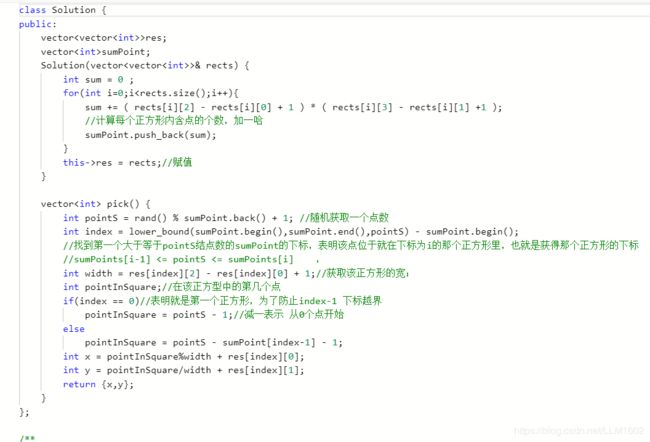
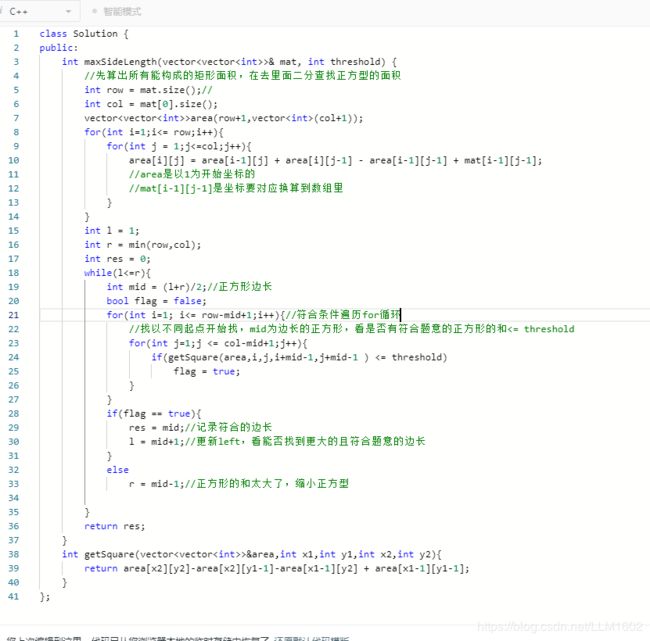
while(l mid = (l+r)/2; for(){}//计数K次符合条件 if() l = mid+1 else r = mid; 四:二分+类似前缀和(想办法凑出二分的思路,难想出来) 1:528 :https://leetcode-cn.com/problems/random-pick-with-weight/ 题目:这题稍微简单好理解一些 思路:因为代表权重,那么可以考虑用区间长度来算权重,怎么来弄区间呢,那可以累加和,比如1,3->sum[0]=1, sum[1]=4,自然而然区间就出来了, 代码: 收获:lower_bound的返回值是迭代器,-begin() ,就是坐标。前面加* 就是对应的值 2:497: https://leetcode-cn.com/problems/random-point-in-non-overlapping-rectangles/ 题目: 思路:很显然用二分感觉不太可能,但是如果以前缀和的思想,就像上一题一样,这里可以把矩形所包含的点的个数累加和,从而就可以用二分了,随机返回一个数量,代表有多少个点,这样就可以定位到是哪个矩形了,从而也就定位那个矩形的某个点了,期间用到lower_bound()了,具体看代码; 代码: 3:1292:https://leetcode-cn.com/problems/maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold/ 题目: 思路:也是前缀和思想,先算出所有的矩形的和,再用二分查找,二分找的是正方形的边长,以该边长去一个个找,也就是全部位置遍历一遍,看是否有符合的,有则返回true;
}