蓝桥杯2013年第四届决赛C_C++程序设计本科B组

1. 猜灯谜

A 村的元宵节灯会上有一迷题： 请猜谜 * 请猜谜 = 请边赏灯边猜 小明想，一定是每个汉字代表一个数字，不同的汉字代表不同的数字。
请你用计算机按小明的思路算一下，然后提交“请猜谜”三个字所代表的整数即可。

2. 连续奇数和

小明看到一本书上写着：任何数字的立方都可以表示为连续奇数的和。 比如： 2^3 = 8 = 3 + 5 3^3 = 27 = 7 + 9 +
11 4^3 = 64 = 1 + 3 + … + 15 虽然他没有想出怎么证明，但他想通过计算机进行验证。 请你帮助小明写出 111
的立方之连续奇数和表示法的起始数字。如果有多个表示方案，选择起始数字小的方案。
思路：奇数的等差序列an=2*n-1，Sn=n^2，只需要找到111^3=m^2-(n-1)^2，n为起始的奇数项，则2*n-1位起始数字。

#include 
using namespace std;
#include 
#include 
#include 
#include  

#define m 111*111*111     
/**列出111立方内的奇数，在求连续的和是否等于111的立方*/
int main()    
{    
    for(int i=1;i<=m/2+3;i+=2)
    {  
        long long sum=0;  
        for(int j=i;j<=m/2+3;j+=2)
        {  
            sum+=j;  
            if(sum==m)
            {  
                cout<return 0;  
            }  
        if(sum>m)  
            break;  
        }  
    }  
    return 0;    
}   

3. 空白格式化

本次大赛采用了全自动机器测评系统。 如果你的答案与标准答案相差了一个空格，很可能无法得分，所以要加倍谨慎！
但也不必过于惊慌。因为在有些情况下，测评系统会把你的答案进行“空白格式化”。其具体做法是：去掉所有首尾空白；中间的多个空白替换为一个空格。所谓空白指的是：空格、制表符、回车符。
以下代码实现了这个功能。仔细阅读代码，填写缺失的部分。

 void f(char* from, char* to) 
 {
     char* p_from = from;
     char* p_to = to;
     while(*p_from==' ' || *p_from=='\t' || *p_from=='\n') 
         p_from++;

     do
     {
         if(*p_from==' ' || *p_from=='\t' || *p_from=='\n')
         {
             do
             {
                 p_from++;
             }
             while(*p_from==' ' || *p_from=='\t' || *p_from=='\n');
             if(____________________) *p_to++ = ' ';  //填空位置
         }
     }while(*p_to++ = *p_from++); 

 }

思路：当中间的多个空白替换为一个空格，并要判断是否判断到’\0’，所以就是填空位置表达的意思。

answer: *p_from

---

4. 高僧斗法

古时丧葬活动中经常请高僧做法事。仪式结束后，有时会有“高僧斗法”的趣味节目，以舒缓压抑的气氛。
节目大略步骤为：先用粮食（一般是稻米）在地上“画”出若干级台阶（表示N级浮屠）。又有若干小和尚随机地“站”在某个台阶上。最高一级台阶必须站人，其它任意。(如图1所示)

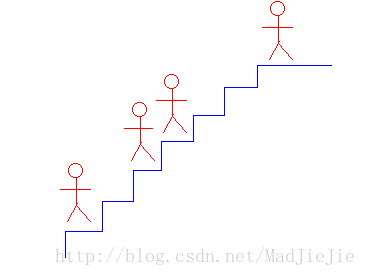
两位参加游戏的法师分别指挥某个小和尚向上走任意多级的台阶，但会被站在高级台阶上的小和尚阻挡，不能越过。两个小和尚也不能站在同一台阶，也不能向低级台阶移动。
两法师轮流发出指令，最后所有小和尚必然会都挤在高段台阶，再也不能向上移动。轮到哪个法师指挥时无法继续移动，则游戏结束，该法师认输。
对于已知的台阶数和小和尚的分布位置，请你计算先发指令的法师该如何决策才能保证胜出。
输入数据为一行用空格分开的N个整数，表示小和尚的位置。台阶序号从1算起，所以最后一个小和尚的位置即是台阶的总数。（N<100,
台阶总数<1000） 输出为一行用空格分开的两个整数: A B,
表示把A位置的小和尚移动到B位置。若有多个解，输出A值较小的解，若无解则输出-1。

例如： 用户输入： 1 5 9 则程序输出： 1 4 再如： 用户输入： 1 5 8 10 则程序输出： 1 3 资源约定： 峰值内存消耗
< 64M CPU消耗 < 1000ms 请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。 注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++
标准，不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include ，
不能通过工程设置而省略常用头文件。

---

尼姆博奕（Nimm Game）：
有三堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

这种情况最有意思，它与二进制有密切关系，我们用（a，b，c）表示某种局势，首
先（0，0，0）显然是奇异局势，无论谁面对奇异局势，都必然失败。第二种奇异局势是
（0，n，n），只要与对手拿走一样多的物品，最后都将导致（0，0，0）。仔细分析一
下，（1，2，3）也是奇异局势，无论对手如何拿，接下来都可以变为（0，n，n）的情 形。

计算机算法里面有一种叫做按位模2加，也叫做异或的运算，我们用符号（+）表示
这种运算。这种运算和一般加法不同的一点是1+1=0。先看（1，2，3）的按位模2加的结 果： 1 =二进制01 2 =二进制10 3
=二进制11 （+） ——————— 0 =二进制00 （注意不进位）
对于奇异局势（0，n，n）也一样，结果也是0。
任何奇异局势（a，b，c）都有a（+）b（+）c =0。 如果我们面对的是一个非奇异局势（a，b，c），要如何变为奇异局势呢？假设 a < b < c,我们只要将 c 变为 a（+）b,即可,因为有如下的运算结果:
a（+）b（+）(a（+）b)=(a（+）a)（+）(b（+）b)=0（+）0=0。要将c 变为a（+）b，只要从 c中减去
c-（a（+）b）即可。

例1。（14，21，39），14（+）21=27，39-27=12，所以从39中拿走12个物体即可达 到奇异局势（14，21，27）。
例2。（55，81，121），55（+）81=102，121-102=19，所以从121中拿走19个物品 就形成了奇异局势（55，81，102）。
例3。（29，45，58），29（+）45=48，58-48=10，从58中拿走10个，变为（29，4 5，48）。
例4。我们来实际进行一盘比赛看看：
    甲:(7,8,9)->(1,8,9)奇异局势
    乙:(1,8,9)->(1,8,4)
    甲:(1,8,4)->(1,5,4)奇异局势
    乙:(1,5,4)->(1,4,4)
    甲:(1,4,4)->(0,4,4)奇异局势
    乙:(0,4,4)->(0,4,2)
    甲:(0.4,2)->(0,2,2)奇异局势
    乙:(0,2,2)->(0,2,1)
    甲:(0,2,1)->(0,1,1)奇异局势
    乙:(0,1,1)->(0,1,0)
    甲:(0,1,0)->(0,0,0)奇异局势
    甲胜。

---

面对奇异局势则必败！ 这道题中，最难的是构造这个取子游戏的模型。 对于 1 5 8 10这个样例，我们把1 5分为一组，8
10分为一组，我们发现，无论5怎么向前移动，后面的1紧跟上来就可以了！ 然而，8怎么移动，5移动，然后1又可以跟着移动，所以说：
**

你移动8是没有意义的！

** 所以我们只需要分析每一组的第二个怎么移动！

关于怎么样可以得到最小的解，就是直接枚举，从最小的情况枚举出来之后，如果该情况的nim答案是0，则说明你移动这一步，对方面对奇异局势，必败！
则输出！

const int maxn=1005;
int a[maxn];
int b[maxn];
int c[maxn];
int d[105];
char str[maxn<<1];

bool solve(int n)
{
    memset(b,0,sizeof(b));
    int coun=0;
    for(int i=1;i<=n;++i)
    {
        if(a[i])
            d[coun++]=i;
    }

    d[coun]=d[coun-1]+1;
    int ans=0;
    for(int i=1;i<=coun;i+=2)
    {
        ans^=(d[i]-d[i-1]-1);
    }

    return ans==0;
}

int main()
{
    gets(str);
    int len=strlen(str);
    int coun=0;

    for(int i=0;iwhile(str[i]<'0'||str[i]>'9')
        {
            ++i;
        }

        int t=0;
        for(;iif(str[i]>='0'&&str[i]<='9')
            {
                t=t*10+str[i]-'0';
            }
            else 
            {
                break;              
            }
        }
        a[coun++]=t;
    }
    int n=a[coun-1];
    a[coun]=a[coun-1]+1;
    int ans=0;

    for(int i=1;i<=coun;i+=2)
    {
        b[i]=a[i]-a[i-1]-1;
        ans^=b[i];
    }

    if(!ans)
    {
        printf("-1\n");
    }
    else
    {
        memset(c,0,sizeof(c));
        for(int i=0;i1;
        }
        bool ans=true;
        for(int i=1;i<=n&&ans;++i)
        {
            memcpy(a,c,sizeof(c));
            for(int j=i+1;j<=n&&ans;++j)
            {
                if(!a[j])
                {
                    a[i]=0;
                    a[j]=1;
                    if(solve(n))
                    {
                        printf("%d %d\n",i,j);
                        ans=false;
                        break;
                    }
                    a[i]=1;
                    a[j]=0;
                }
                else break;
            }
        }
    }


    return 0;
}

5. 格子刷油漆

X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形（如图1所示），现需要把这些格子刷上保护漆。你可以从任意一个格子刷起，刷完一格，可以移动到和它相邻的格子（对角相邻也算数），但不能移动到较远的格子（因为油漆未干不能踩！） 比如：a d b c e f 就是合格的刷漆顺序。 c e f d a b 是另一种合适的方案。 当已知 N 时，求总的方案数。当N较大时，结果会迅速增大，请把结果对 1000000007 (十亿零七) 取模。 输入数据为一个正整数（不大于1000） 输出数据为一个正整数。

例如：
用户输入：
2
程序应该输出：
24
再例如：
用户输入：
3
程序应该输出：
96
再例如：
用户输入：
22
程序应该输出：
359635897
资源约定：
峰值内存消耗 < 64M
CPU消耗 < 1000ms
请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

---

思路：这道是个递推题。暴力搜索复杂度太高，指数级别的。这个公式推了好久，因为情况比较多。2*N的出发的起点格子一共有2种类型。

1、四个角。设b[n]表示边缘一列的一个角的格子出发，遍历全体格子后，结束点再该列的种类数 b[1]=1 b[n]=b[n-1]*2 ，a[n]表示长度为n的一个角的格子出发，遍历全体格子的种类数 ： a[1]=1 a[2]=6 a[n]=2*a[n-1]+4*a[n-2]+b[n] （n>2） +2*a[n-1]表示如果第二个涂油漆的点和出发点是同一列。+4*a[n-2]表示和出发点是同一列的格子是第三次涂的，它要先经过前一列周转之后才涂，涂完之后前一列也就涂完了，就剩下n-2列没有涂，乘以4是因为第二次涂的格子有2种，然后开始从n-2列开始涂的时候又有两个选择，根据乘法原理2*2. 。 +b[n] 表示和出发点是同一列的格子是最后一次才涂的。

2、除了四个角的其余格子。设 c[i]表示从中间(1 < i < n)的某一列出发， 遍历全体格子的种类数 c[i]=2*b[i]*2*a[n-i]+2*b[n-i+1]*2*a[i-1] 加号左边表示县遍历左边的格子，加号右边的式子表示先遍历右边的格子 ，因为先出发的那一边必须回到出发的那一列，而往后就是不收限制即a[n]的情况了 。

结果的答案就是 num=4*a[n]+sum(c[i]) 1

    #include  
    #include   
    #include  

    const int MOD =1000000007;   

    using namespace std;  

    // a[n]表示最边缘一列的一个角的格子出发，遍历全体格子的种类数   a[1]=1   a[2]=6  a[n]=2a[n-1]+4a[n-2]+b[n]  n>2  
    // b[n]表示边缘一列的一个角的格子出发，遍历全体格子后，结束点再该列的种类数  b[1]=1  b[n]=b[n-1]*2   
    // c[i]表示从中间的格子出发， 遍历全体格子的种类数  c[i]=2*b[i]*2*a[n-i]+2*b[n-i+1]*2*a[i-1]  加号左边表示县遍历左边的格子，加号右边的式子表示先遍历右边的格子 ，因为先出发的那一边必须回到出发的那一列，而往后就是不收限制即a[n]的情况了   
    long long a[1010]={0};  
    long long b[1010]={0};  
    long long c[1010]={0};  
    int main()  
    {  

        int n;  
        long long num=0;  
        a[1]=1;  
        a[2]=6;  
        b[1]=1;  
        b[2]=2;  
        cin>>n;  

        for(int i=3;i<=n;i++)  
        {  
            b[i]=b[i-1]*2%MOD;  
            a[i]=((2*a[i-1])%MOD+(4*a[i-2])%MOD+b[i]%MOD)%MOD;  
        }  
        for(int i=2;i<=n;i++)  
        {  
            c[i]=4*((b[i]*a[n-i])%MOD+(b[n-i+1]*a[i-1])%MOD)%MOD;  
        }  
        num=4*a[n]%MOD;  
        for(int i=2;i%MOD);  
            num%=MOD;  
        }  

        cout<return 0;  
    }